
- •1. Компоновка. Требования к компоновке. Конструктивная иерархия в конструкциях радиоустройств. Уровни компоновки аппаратуры радиотехнического назначения. Виды блоков.
- •2. Назначение и виды электрических соединений в конструкциях. Требования. Печатные электрические соединения. Достоинства и недостатки. Определения.
- •3. Материалы и методы изготовления печатных плат (пп).
- •4. Методы конструирования печатных плат.
- •5. Требования к размерам пп. Координатная сетка. Собственная резонансная частота пп.
- •6. Элементы печатного рисунка и их параметры.
- •7. Постоянный и переменный ток в печатном проводнике. Правила размещения печатных проводников.
- •8. Влияние старения на параметры печатных плат.
- •1. Причины искажений сигналов в цепях радиоустройств. Электрически короткие и электрически длинные линии связи.
- •2. Электрические параметры линий связи. Связь конструктивных и электрических параметров линий связи.
- •1. Дестабилизирующие факторы.
- •2. Виды допусков электрических параметров радиоустройств.
- •3. Связь параметров поля допуска и числовых характеристик случайных величин.
- •4. Уравнение абсолютных и относительных погрешностей.
- •5. Систематическая составляющая относительной погрешности выходного параметра.
- •6. Случайная составляющая относительной погрешности выходного параметра.
- •7А. Расчет производственного допуска.
- •7. Уравнение погрешностей, вызванных воздействием окружающей среды.
- •8. Расчет допуска влажности.
- •9. Расчет температурных допусков.
- •10. Расчет допуска старения.
- •11. Эксплуатационный допуск. Систематическая составляющая.
- •12. Эксплуатационный допуск. Случайная составляющая.
- •1. Надежность, безотказность, отказ, виды отказов, априорная и апостериорная теория надежности.
- •2. Вероятность безотказной работы
- •3. Среднее время наработки до первого отказа.
- •4. Вероятность безотказной работы.
- •5. Интенсивность отказов. Интенсивность отказов для распределения Вейбулла и экспоненциального распределения.
- •6. Зависимость вероятности безотказной работы и интенсивности отказов
- •7. Распределение Вейбулла.
- •8. Экспоненциальное распределение. Его особенности.
- •9.Последовательное соединение элементов.
- •10.Параллельное соединение элементов. Резервирование
- •11. Учет условии эксплуатации при расчете надежности.
- •12. Порядок расчета надежности функционального узла радиоконструкции.
- •1. Дестабилизирующие факторы.
- •2. Герметичность конструкций, степень негерметичности, течь, утечка, натекание. Нормы гарметичности.
- •3. Защита конструкций монолитными и полыми оболочками в аппаратуре 3-его поколения.
- •4. Защита конструкций полыми оболочками с демонтируемым паяным швом
2. Вероятность безотказной работы
Поскольку в теории надежности отказ
является событием случайным, то для его
описания использую случайную величину
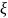 - время наработки до первого отказа.
- время наработки до первого отказа.
![]()
0 – момент включения устройства; t – время проведения измерений на наличие отказов.
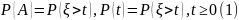 ,
событие А:
,
событие А:
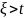
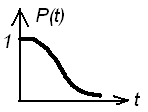
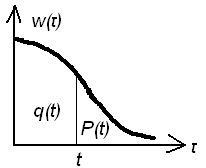
P(t) – вероятность безотказной работы – основная характеристика безотказности, представляющая собой вероятность того, что время наработки будет превышать заданный интервал от 0 до t.
t->0 => P(t)->1; t->беск. =>P(t)->0
Вероятность отказа
Рассмотрим событие
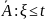 ,
- случайная величина, наработка до
первого отказа.
,
- случайная величина, наработка до
первого отказа.
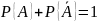
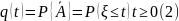
q(t) – вероятность отказа на заданном временном интервале [0,t].
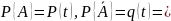
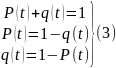
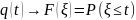 .
.
а) возрастающая функция своего аргумента.
б) t=0 q(t)=0
в) t->беск q(t)->1
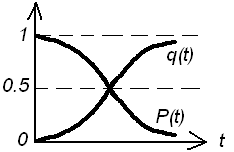
Плотность вероятности момента первого отказа.
Поскольку непрерывная случайная величина, а q(t) – непрерывная и дифференцируемая функция, то можно получить плотность распределения
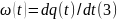 ,
,

 –плотность вероятностей момента первого
отказа.
–плотность вероятностей момента первого
отказа.
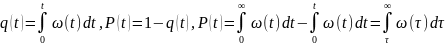
3. Среднее время наработки до первого отказа.
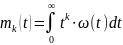
Хотя q(t) и w(t) полностью характеризуют , однако на практике используют числовые характеристики: матожидание, дисперсия.
Найдем МО .
 -среднее время наработки до первого
отказа.
-среднее время наработки до первого
отказа.
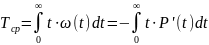
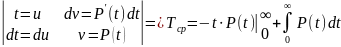
Рассмотрим конечное


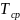 широко используется для сравнительной
оценки вариантов технических решений.
По значению
возможно восстановить кривую P(t)
широко используется для сравнительной
оценки вариантов технических решений.
По значению
возможно восстановить кривую P(t)
Среднее время наработки для экспоненциального распределения.
Экспоненциальное распределение
вероятности безотказной работы является
частным случаем распределения Вейбулла
при
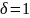
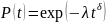
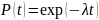
Определяется одним параметром
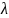
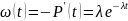

Экспоненциальное распределение позволяет
описать вероятность безотказной работы
на этапе эксплуатации системы. Для
экспоненциального распределения
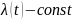 .
.
Найдем для экспоненциального распределения
среднее время наработки до первого
отказа используя соотношение

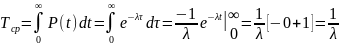
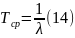
Для экспоненциального распределения среднее время наработки и интенсивность отказа связаны зависимостью (14). [1/час] [кол-во отказов/час].
Особенности экспоненциального распределения.
Из соотношения
,
учтя
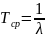 ,
получим
,
получим
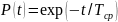 .
.
 .
.
Для экспоненциального распределения
время нормальной эксплуатации меньше
среднего времени наработки до первого
отказа. Найдем для экспоненциального
распределения
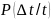
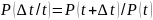
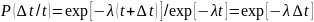
Учитывая вероятность безотказной работы
на интервале
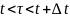 определяется лишь длиной интервала и
не зависит от начала отсчета, т.е. t
может иметь любые значения.
определяется лишь длиной интервала и
не зависит от начала отсчета, т.е. t
может иметь любые значения.
Экспоненциальное распределение не учитывает фактор старения, оно является идеализированной моделью, которая лишь с некоторым приближением позволяет оценить вероятность появления внезапных отказов, поэтому экспоненциальное распределение используется в основном в априорной теории надежности для сравнительной оценки разрабатываемых/проектируемых вариантов технических решений.
Основное достоинство – простота расчетов. Использование экспоненциального распределения в апостериорной теории надежности возможно лишь при проверке результатами испытаний данных полученных при использовании экспоненциальных распределений.
