29. Интеграл с переменным верхним пределом. Сформулировать теорему Барроу. Формула Ньютона-Лейбница Интеграл с переменным верхним пределом

 

Пусть на отрезке [ a, b ] задана непрерывная функция  f ( x ), тогда для любого x   [ a, b ] существует функция: 

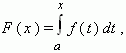
задаваемая  интегралом с переменным верхним пределом, стоящим в правой части равенства.

 

На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.

Теорема Барроу

Если интегрируема на и непрерывна в точке то функция 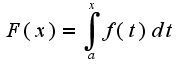дифференцируема в точке x0 и

Формула

Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:

Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда 

Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разностьF (b) – F (a).

29. Способы вычисления определенного интеграла: интегрирование по частям, замена переменной, интеграл, взятый по симметричному интервалу

Способы:

-Замена переменной в определенном интеграле

Если функция x = x(u) непрерывно дифференцируема на интервале  , а функция f(x) непрерывна на интервале  , где m - точная нижняя, а M - точная верхняя граница функции x(u) на интервале  , то

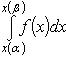
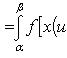
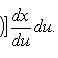
- Интегрирование по частям

Интегрирование по частям 

или

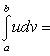
(u, v непрерывно дифференцируемы на интервале  ).

29. Вычисление площади плоской фигуры в декартовой и полярной системах координат

 Площадь плоской фигуры в декартовых координатах

Допустим, что фигура предполагает наличие границы

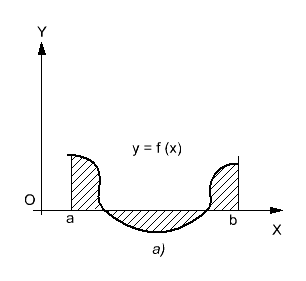
является криволинейной трапецией и , при условии, что на

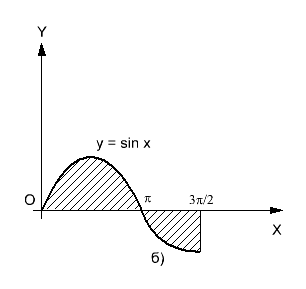
Если находится ниже оси (рис. 18.1), то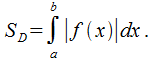

На плоскости можно рассмотреть полярную систему координат  . Тогда точке   соответствуют координаты   и  , предполагаем полуоси   и   ( ) совпадающими; причем    положительное  направление угла    – против вращения часовой стрелки.

Ф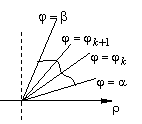 игура на плоскости, ограниченная лучами  ,   ( ) и кривой  ,  , называется криволинейным сектором. Очевидно, при    имеет круговой сектор и его площадь  . Поэтому если провести процедуру построения интегральной суммы   для разбиения  ,  ,   и системы точек  , то при  , где  ,  , придем к интегралу  , который можно  интерпретировать как площадь криволинейного сектора.

Итак, если предел интегральной суммы, построенной по указанной процедуре, существует, то площадь криволинейного сектора можно вычислить по формуле .

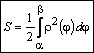29. Вычисление длины кривой