
Билет №1.
Первообразная функции и неопределенный интеграл.
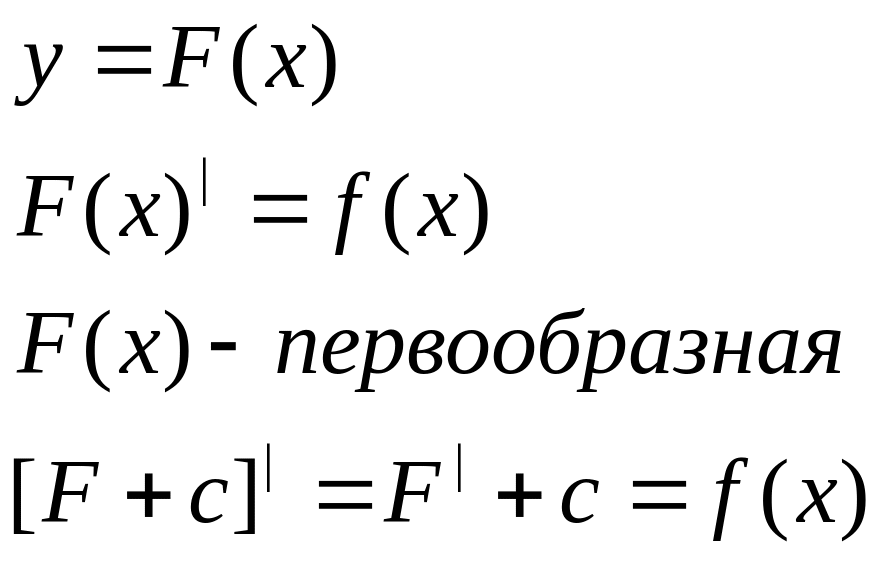
Терема:
Если F(x) яв –ся первообразной от фун-ции f(x), то и F(x)+c тоже яв-ся первообразной f(x).
Совокупность первообр. {F(x)+c} называют неопределенным итегралом.
![]()
![]()
![]() -знак
интеграла
-знак
интеграла
![]() -
подинтегральная ф-ция;
-
подинтегральная ф-ция;
![]() -
подинтегральное выражение;
-
подинтегральное выражение;
x- переменная интегрирования;
c- постоянная;
Билет2.
Свойства неопределённого интеграла.
1)![]()
Док-
во:
![]()
2)![]()
3)![]() Док-во:
Док-во:
![]() (из
определения диф-ла)
(из
определения диф-ла)
4)![]() Док-во:
Док-во:
![]()
5)![]()
Док-во:
![]()
![]()
4),5)- линейные свойства неопределённого интеграла
Билет №3.
Интегралы от основных элементарных функций.(таблица)

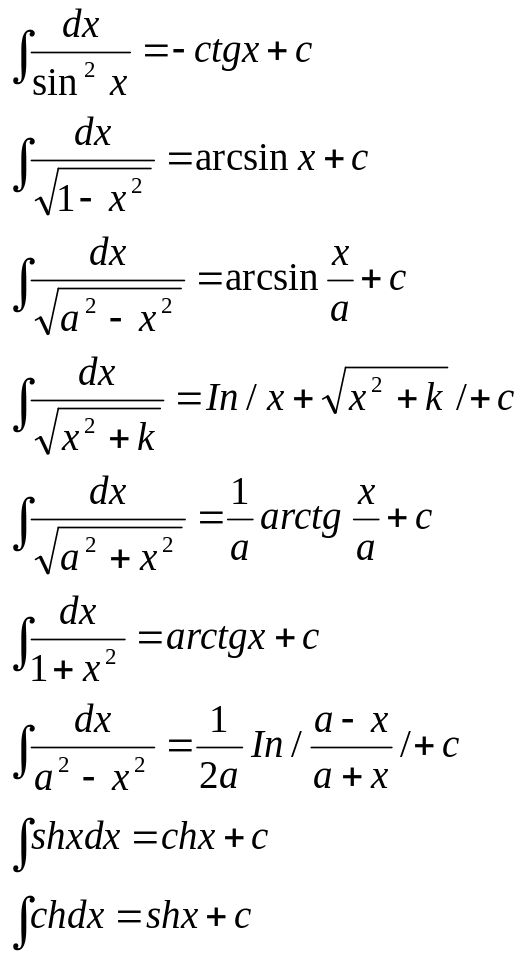
Билет №4.
Метод замены переменной в неопределённом интеграле
Теорема:
Если
ф-ия x(t)
диф-ма на мн- ве t![]() T
и сущ.
T
и сущ.![]() ,
то
,
то
![]()
Док- во:
![]()
![]()
Билет 5.
Метод интегрирования по частям.
Теорема.
Пусть ф-ция u=u(x) дифференцируема на x X, а ф-ция v=v(x) интегрируема на мн-ве x, тогда справедлива формула интегрирования по частям:
![]()
Док-во:

![]()
Типы интегралов:
1.

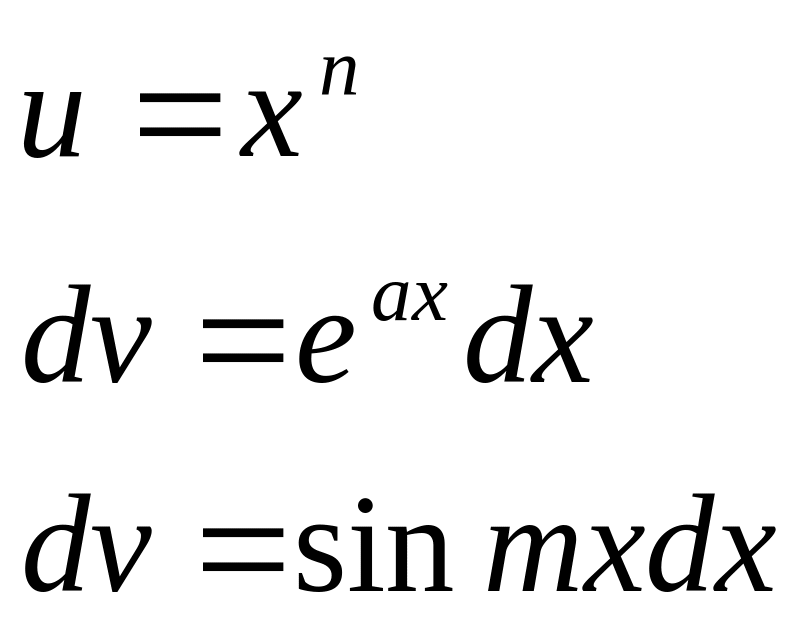
нужно применять формулу интегрирования по частям n раз
2.

![]()
применять ф-лу k раз;
Билет №6.
Интегрирование простейших рациональных дробей
![]()
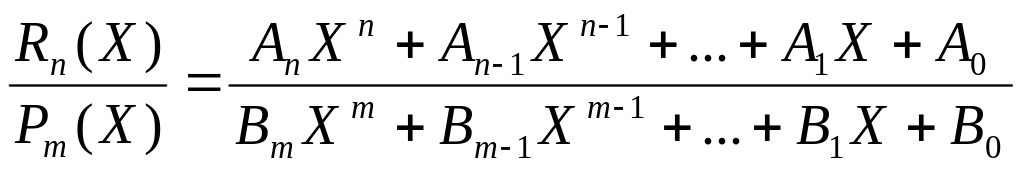
1)n>m=>неправильная дробь, нужно выделить у этой дроби целую часть и правильную дробь.
![]() ,
где W(X)-
целая часть.
,
где W(X)-
целая часть.
Метод вычёркивания можно использовать только в том случае, если знаменатель представлен в виде произведения полиномов первых степеней.
Билет №7.
Интегрирование некоторых видов иррациональностей.
Интегралы
вида
![]() ,
,![]() .
.
а) -интегралы, подинтегральная
фун-ция кот-рых яв-ся иррациональной
ф-цией
относительно
![]() .
.
![]()
б)
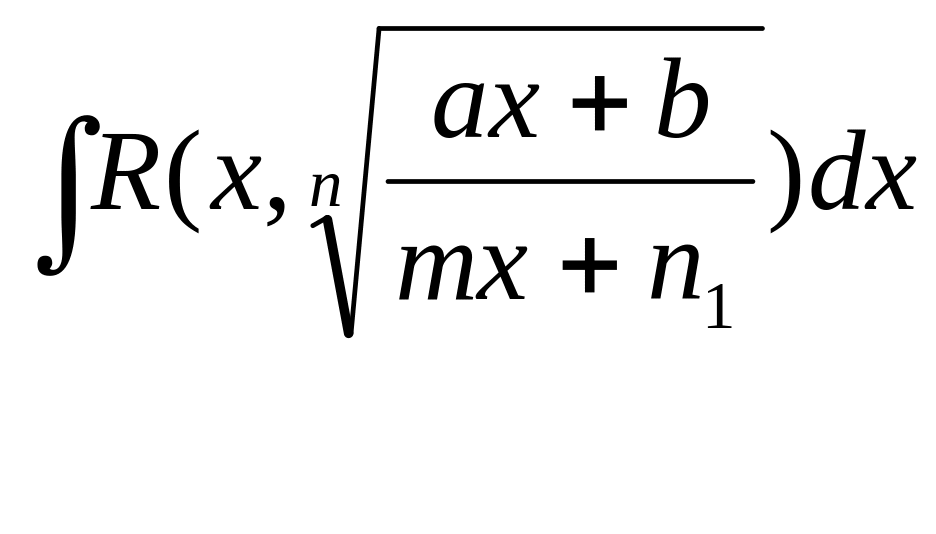
![]()
![]()
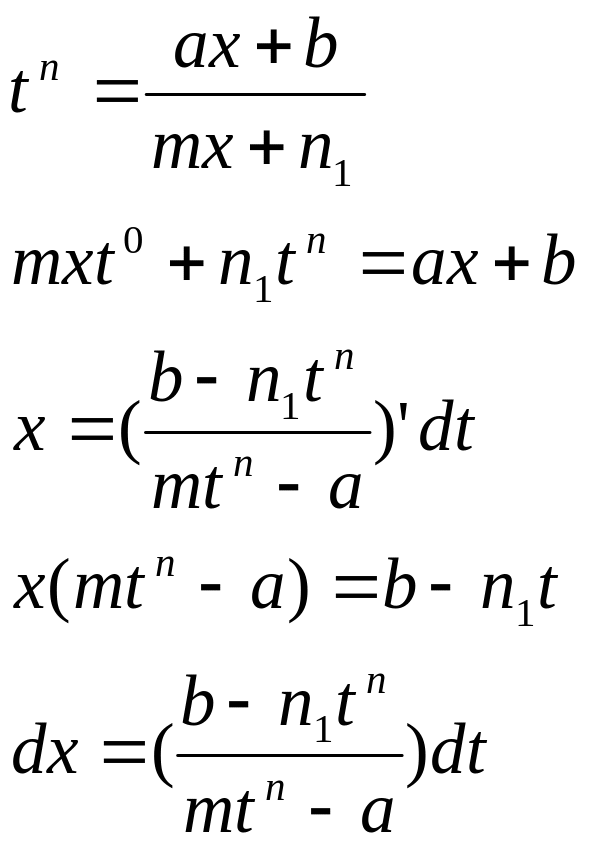
Билет №8.
Интеграл
вида
![]()
Подстановка
Эйлера: 1-ая подстановка: a>0
![]()
![]()
X=![]()
![]()
2-ая
подстановка: с>0
![]() (или
(или
![]() )
)
Замечание: подстановки Эйлера не рекомендуются, если a>0 и c>0 одновременно.
3-ая
подстановка:
![]()
Билет№9.
Интегрирование тригонометрических ф-ций.
![]() -интегралы,
к-рые считаются рациональными отностельно
sinx
и cosx.
-интегралы,
к-рые считаются рациональными отностельно
sinx
и cosx.
Универсальная подстановка:
![]()
Замечание: универсальная подстановка приводит часто к громоздким вычислениям и , поэтому лучше использовать спец. приемы.

Билет №10.
Интегрирование иррациональных функций с помощью тригонометрических подстановок.
Замечание:
универсальная подстановка хорошо
применяется для интегралов вида:
![]() а в остальных случаях применение
универсальной подстановки громоздко.
а в остальных случаях применение
универсальной подстановки громоздко.
Интегралы
вида:
![]()
![]()
1)если
m-
нечётное, n-
чётное, то замена
![]()
2)если
m-
чётное, n-
нечётное, то замена
![]()
3)если m,n- нечётные, то замена или
4)если
m,n-
чётные, то необходимо понизить степень
при помощи формул
![]() ;
;
![]() и
и
![]()
5)если
m+n=-2k,
гдеk>0
и
![]() m+n<0
, то замена t=tgx
m+n<0
, то замена t=tgx
Билет №11.
Интегрирование дифференциальных биномов.
![]()
1)p![]() x=
x=![]() ,
n-
общий знаменатель дроби
,
n-
общий знаменатель дроби
2)![]()
![]() общий
знаменатель m
и n
общий
знаменатель m
и n
3)
![]()
![]() ,
где s-
знаменатель p
,
где s-
знаменатель p
Билет №12.
Интегралы, неберущиеся в элементарных функциях.
1)
![]() -
интеграл Пуассона (статистика) 2)
-
интеграл Пуассона (статистика) 2)
![]() -интегральный
sin
-интегральный
sin
3)![]() -интегральный
cos 4)
-интегральный
cos 4)![]() -интеграл
Френеля
-интеграл
Френеля
5)![]() -интеграл
Френеля
-интеграл
Френеля
Билет 13.
Понятие определенного интеграла, его геометрический смысл. Нижняя и верхняя интегральные суммы
Пусть
функция
![]() определена на отрезке
определена на отрезке
![]() ,a<b.
Разобьем этот отрезок на n
произвольных частей точками
,a<b.
Разобьем этот отрезок на n
произвольных частей точками
![]()
Обозначим
это разбиение через
![]() ,
а точки
,
а точки
![]() будем называть точками разбиения. В
каждом из полученных частичных отрезков
будем называть точками разбиения. В
каждом из полученных частичных отрезков
![]() выберем произвольную точку
выберем произвольную точку
![]() .
Через
.
Через
![]() обозначим разность
обозначим разность
![]() ,
которую будем называть длиной частичного
отрезка
.
,
которую будем называть длиной частичного
отрезка
.
Составим сумму
![]() (1)
(1)
которую назовем интегральной суммой для функции f(x) на [a,b], соответствующей данному разбиению [a,b] на частичные отрезки и данному выбору промежуточных
точек
![]() .
Геометрический смысл суммы очевиден:
это сумма площадей прямоугольников с
основаниями
.
Геометрический смысл суммы очевиден:
это сумма площадей прямоугольников с
основаниями
![]() и высотами
и высотами
![]() ,
если f(x)>=0.
,
если f(x)>=0.
Обозначим
через
![]() длину наибольшего частичного отрезка
разбиения
:
длину наибольшего частичного отрезка
разбиения
:
![]() .
.
Определение:Если
существует конечный предел I
интегральных сумм (1) при
![]() ,
то этот предел называется определенным
интегралом от функции f(x)
по отрезку [a,b]
и обозначается следующим образом:
,
то этот предел называется определенным
интегралом от функции f(x)
по отрезку [a,b]
и обозначается следующим образом:
![]() т.е.
т.е.
![]()
В этом случае функция f(x) называется интегрируемой на [a,b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, x – переменной интегрирования.
Билет 14.
Свойства определенного интеграла
По определению
![]()
По определению
![]()
Каковы бы ни были числа a, b, c, всегда имеет место равенство
![]()
Постоянный множитель можно выносит за знак определенного интеграла, т.е.
![]()
Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е.
![]()
Формулы оценки определенных интегралов
Будем
полагать, что
![]() .
.
1.
Если
![]() всюду на отрезке
всюду на отрезке
![]() ,
то
,
то
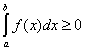 .
.
2.
Если
![]() всюду на отрезке
,
то
всюду на отрезке
,
то
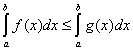 .
.
3.
Если
![]() интегрируема на отрезке
,
то
интегрируема на отрезке
,
то
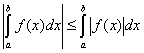 .
.
4.
Если
![]() и
и
![]() - соответственно максимум и минимум
функции
на отрезке
,
то
- соответственно максимум и минимум
функции
на отрезке
,
то
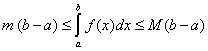 .
.
Билет 15.
Определенный интеграл как функция верхнего предела
Если
функция
интегрируема на отрезке
,
то она интегрируема и на отрезке
![]() ,
где
,
где
![]() .
Рассмотрим функцию аргумента
.
Рассмотрим функцию аргумента
![]()
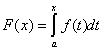 . (1)
. (1)
Назовем
функцию
![]() интегралом с
переменным верхним пределом.
В формуле (1) переменная интегрирования
обозначена буквой
интегралом с
переменным верхним пределом.
В формуле (1) переменная интегрирования
обозначена буквой
![]() ,
чтобы избежать путаницы с переменным
верхним пределом
.
,
чтобы избежать путаницы с переменным
верхним пределом
.
Теорема: Непрерывная на отрезке функция имеет на этом отрезке первообразную. Одной из первообразных является функция
.
Таким образом, любая непрерывная на отрезке функция имеет на этом отрезке первообразную в форме определенного интеграла с переменным верхним пределом. Поскольку всякая другая первообразная отличается от на постоянную величину, то связь между неопределенным и определенным интегралами имеет вид
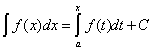 ,
,
где С – произвольная постоянная.
Билет 16.
Формула Ньютона-Лейбница. Замена переменной в определенном интеграле
Теорема: Пусть функция f(x) непрерывна на отрезке [a,b]. Тогда, если функция F(x) является некоторой ее первообразной на этом отрезке, то справедлива следующая формула:
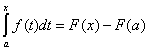
Эта формула называется формулой Ньютона – Лейбница.
Вывод формулы:
Непрерывная на отрезке функция имеет на этом отрезке первообразную, которая определяется формулой
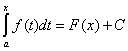 , (1)
, (1)
где
С
– произвольная постоянная. Подставляя
![]() в формулу (1), получаем с учетом свойства
(1) определенного интеграла:
в формулу (1), получаем с учетом свойства
(1) определенного интеграла:
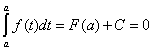 ,
,
откуда
![]() .
.
Тогда из выражения (1) имеем
.
Полагая
теперь
![]() ,
получаем формулу
,
получаем формулу
 . (2)
. (2)
Равенство (2) называется основной формулой интегрального исчисления, или формулой Ньютона-Лейбница.
Разность
![]() условно записывают символом
условно записывают символом
![]() .
Формула (2) дает широкие возможности
для вычисления определенных интегралов.
.
Формула (2) дает широкие возможности
для вычисления определенных интегралов.
Пусть:
1)
- непрерывная функция на отрезке
![]() ;
;
2)
функция
![]() дифференцируема на
дифференцируема на
![]() ,
а
,
а
![]() непрерывна на
;
непрерывна на
;
3)
![]() ,
,
![]() .
.
Тогда справедлива формула
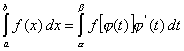 (3)
(3)
Формула (3) называется формулой замены переменной или подстановки в определенном интеграле.
Заметим, что при вычислении определенного интеграла с помощью замены переменной нет нужды возвращаться к прежней переменной, как при вычислении неопределенного интеграла, так как определенный интеграл представляет собой число, которое, согласно формуле (3) равно значению каждого из рассматриваемых интегралов. Теперь при подстановке следует сначала найти новые пределы интегрирования и выполнить необходимые преобразования подынтегральной функции.
Билет 17.
Формула интегрирования по частям в определенном интеграле
Теорема:
Пусть функции u=u(x) и v=v(x) имеют на отрезке [a,b] непрерывные производные u`(x) и v`(x). Тогда имеет место равенство
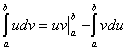
В силу условия теоремы произведение uv=u(x)v(x) данных функций имеет на [a,b] производную, равную
(uv)`=uv`+vu`, т.е. является первообразной на [a,b] для функции uv`+vu`. Применяя формулу Ньютона-Лейбница, получим
![]() .
Отсюда находим
.
Отсюда находим
![]()
Так как по определению дифференциала функции v`dx=dv, u`dx=du то окончательно будем иметь
Билет 18.
Вычисление площадей плоских фигур с помощью определенного интеграла
Пусть
функция
![]() неотрицательна и непрерывна на отрезке
.
Тогда по геометрическому смыслу
определенного интеграла площадь S
под кривой
на
численно равна определенному интегралу
неотрицательна и непрерывна на отрезке
.
Тогда по геометрическому смыслу
определенного интеграла площадь S
под кривой
на
численно равна определенному интегралу
 ,
т.е.
,
т.е.
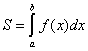 .
.
Пример:
Найти
площадь фигуры, ограниченной линиями
![]() ,
,
![]() ,
,
![]() .
.
Из
Рис. 1 видно, что площадь криволинейного
треугольника ОАВ равна разности двух
площадей:
![]() .
Решая систему
.
Решая систему
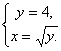 ,
получаем координаты точки В (точки
пересечения кривой
и прямой
)
В
,
получаем координаты точки В (точки
пересечения кривой
и прямой
)
В![]() .
Тогда
.
Тогда
 ,
,
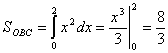 .
.
Окончательно
![]() .
.
Отметим, что данная задача может быть решена другим способом.
По
определению определенного интеграла
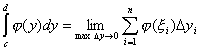 .
.
Это
равенство можно понимать так, что при
построении интегральной суммы разбиению
подвергается отрезок
![]() оси ординат. Соответственно точки
оси ординат. Соответственно точки
![]() - это ординаты, фиксированные на каждом
из отрезков разбиения. Поэтому, если
- это ординаты, фиксированные на каждом
из отрезков разбиения. Поэтому, если
![]() на
,
то интеграл
на
,
то интеграл
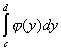 численно равен площади криволинейной
трапеции, ограниченной кривой
численно равен площади криволинейной
трапеции, ограниченной кривой
![]() и прямыми
,
и прямыми
,
![]() ,
,
![]() .
.
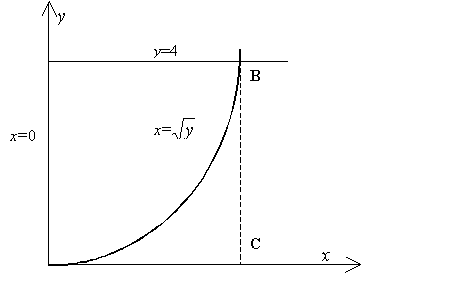
Рис. 1
Возвращаясь к нашей задаче, можно посчитать площадь следующим образом:
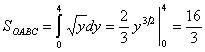 .
.
Если
функция
не
положительна и непрерывна на отрезке
![]() ,
то площадь
,
то площадь
![]() над кривой
на
отличается знаком от определенного
интеграла
над кривой
на
отличается знаком от определенного
интеграла
 :
:
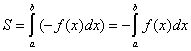 .
.
Пример:
Найти
площадь фигуры, ограниченной линиями
![]() ,
,
![]() ,
,
![]() .
.
Из
Рис. 2 видно, что искомая площадь
криволинейного треугольника ОАВ может
рассматриваться как площадь над кривой
ОАВ на отрезке
![]() .
Однако указанная кривая (ломаная)не
задается одним уравнением. Поэтому для
нахождения площади необходимо разбить
треугольник ОАВ на две части
.
Однако указанная кривая (ломаная)не
задается одним уравнением. Поэтому для
нахождения площади необходимо разбить
треугольник ОАВ на две части
![]() .
Координаты точек есть
.
Координаты точек есть
![]() ,
,
![]() и
и
![]() .
.
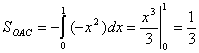 ,
,
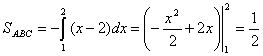 .
.
Окончательно,
![]() .
.

Билет 19.
Вычисление
объемов тел вращения![]()

13.4.1.
Вычисление объёма тела по площадям
поперечных сечений. Пусть тело V
расположено в пространстве между
плоскостями x
= a
и x
= b,
и для
![]() известна
площадь его поперечного сечения
известна
площадь его поперечного сечения
S = S(x). Требуется определить объём этого тела. Рассечём это тело плоскостями x = x0 = a, x = x1, x = x
2, …, x = xi-1, x = xi, …, x = x n-1, x = xn = b на n слоёв (a
= x0< x1 < < x2< …< xn-1 < xn = b), на каждом из
отрезков
[xi-1,
xi]
возьмём произвольную точку
![]() ;
;
будем считать, что объём слоя, заключенного между плоскостями x = xi-1 и x = xi приближённо равен
объёму
![]() цилиндрика
с площадью основания
цилиндрика
с площадью основания
![]() и
высотой
и
высотой
![]() :
:
![]() .
.
Сумма
объёмов
-
объём ступенчатой фигуры - при
![]() стремится
к искомому объёму V,
поэтому
стремится
к искомому объёму V,
поэтому
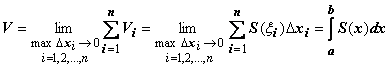 .
13.4.2.
Объём тела, получающегося при вращении
кривой вокруг координатной о
.
13.4.2.
Объём тела, получающегося при вращении
кривой вокруг координатной о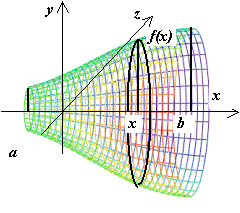 си.
Если объём V
получается в результате вращения кривой
y =
f(x),
си.
Если объём V
получается в результате вращения кривой
y =
f(x),
![]() ,
вокруг оси Ox,
то, очевидно,
,
вокруг оси Ox,
то, очевидно,
![]() ,
поэтому
,
поэтому
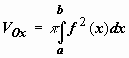 .
Пример:
найти объём эллипсоида, получающегося
при
.
Пример:
найти объём эллипсоида, получающегося
при
вращении
эллипса
 вокруг
оси Ox.
Решение:
эту задачу проще решить, если применить
параметрические уравнения эллипса:
вокруг
оси Ox.
Решение:
эту задачу проще решить, если применить
параметрические уравнения эллипса:
![]() .
.
Верхняя дуга эллипса получается при изменении t от 0 до
![]() ,
при этом точке крайней левой точке
эллипса соответствует значение параметра
t0
, равное
,
крайней
,
при этом точке крайней левой точке
эллипса соответствует значение параметра
t0
, равное
,
крайней
правой
точке соответствует значение tk
= 0. Формула
для
кривой, заданной параметрически,примет
вид
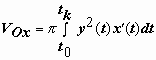 ,
поэтому
,
поэтому
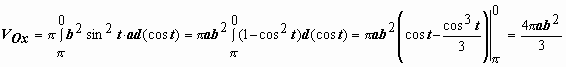 .
Если
требуется найти объём тела, которой
получается при вращении плоской фигуры
ABCD
вокруг оси Oy,
рассуждаем по другому. Разбиваем тело
на полые цилиндры радиуса x,
толщины
.
Если
требуется найти объём тела, которой
получается при вращении плоской фигуры
ABCD
вокруг оси Oy,
рассуждаем по другому. Разбиваем тело
на полые цилиндры радиуса x,
толщины
![]() ,
высоты f(x).
Объём этого цилиндра равен произведению
длины окружности
,
высоты f(x).
Объём этого цилиндра равен произведению
длины окружности
![]() на
толщину
и
высоты f(x);
суммируя эти объёмы и переходя к пределу
при
,
получим
на
толщину
и
высоты f(x);
суммируя эти объёмы и переходя к пределу
при
,
получим
 .
.
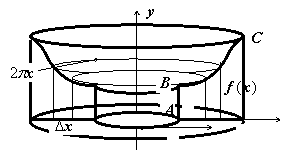
13.4.3.
Объём тела, получающийся при вращении
сектора, ограниченного кривой
![]() и
двумя полярными радиусами
и
двумя полярными радиусами
![]() и
и
![]() ,
вокруг полярной оси находится
по формуле
,
вокруг полярной оси находится
по формуле
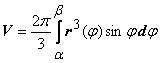
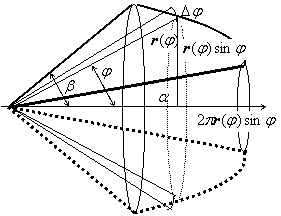 .
Пример:
найти объём тора, полученного вращением
окружности
.
Пример:
найти объём тора, полученного вращением
окружности
![]() вокруг
полярной оси.
вокруг
полярной оси.
Решение:
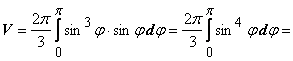
 .
.
Билет 20.
Площадь криволинейного сектора
Пусть кривая АВ задана в полярных координатах уравнением
![]()
![]() ,
,
причем
функция
![]() непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке
![]() .
Плоскую фигуру, ограниченную полярными
радиусами, составляющими с полярной
осью углы
.
Плоскую фигуру, ограниченную полярными
радиусами, составляющими с полярной
осью углы
![]() и
и
![]() ,
будем называть криволинейным сектором
(рис 1). Площадь криволинейного сектора
можно вычислить по формуле
,
будем называть криволинейным сектором
(рис 1). Площадь криволинейного сектора
можно вычислить по формуле
![]()
Рис 1.

Билет 21.
Длина дуги плоской кривой
Пусть
плоская кривая АВ задана уравнением
![]() ,
где f(x)
– непрерывная на отрезке [a,b]
функция. Разобьем кривую АВ на n
произвольных частей точками
,
где f(x)
– непрерывная на отрезке [a,b]
функция. Разобьем кривую АВ на n
произвольных частей точками
![]() = B
в направлении от А к В. Соединив эти
точки хордами, получим некоторую
вписанную ломаную линию, периметр
которой обозначим через Р. Обозначим
через li
длину одного звена
= B
в направлении от А к В. Соединив эти
точки хордами, получим некоторую
вписанную ломаную линию, периметр
которой обозначим через Р. Обозначим
через li
длину одного звена
![]() ломаной линии, а через
ломаной линии, а через
![]() - длину наибольшего из ее звеньев:
- длину наибольшего из ее звеньев:
![]()
Определение.
Число
L
называется пределом периметров Р при
![]() ,
если для любого
,
если для любого
![]() существует
существует
![]() такое, что для всякой ломаной, у которой
такое, что для всякой ломаной, у которой
![]() ,
выполняется неравенство
,
выполняется неравенство
![]()
Если
при
существует конечный предел L
периметра Р вписанной в кривую ломаной
линии, то этот предел называется длиной
дуги
![]() :
:
![]()
Если функция f(x) непрерывна вместе с f `(x) на отрезке [a,b], то длина дуги выражается формулой
![]()
Билет 22.
Площадь поверхности вращения
Площадь поверхности вращения, образующейся при вращении вокруг оси Ox дифференцируемой кривой, определяется по формулам (в зависимости от способа задания кривой)
(
![]() -
длина окружности кольца,
-
длина окружности кольца,
![]() -
его ширина).
Пример:
-
его ширина).
Пример:
найти
площадь тора, образующегося при вращении
окружности
вокруг
оси Ox.
Решение:
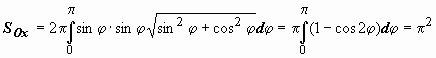 .
.
Билет №24
Вычисление статических моментов, моментов инерции. Координаты центра тяжести
![]()
M=![]() ; Sin(rF)=1; F=ma, |a|=1;
; Sin(rF)=1; F=ma, |a|=1;
M=|r|[m].
![]() ;
;
![]()
Если M действует на дугу y=f(x):
![]()
![]() ;
; ![]()
Центр
масс:
![]()
![]()
![]() p(x)-плотность
p(x)-плотность
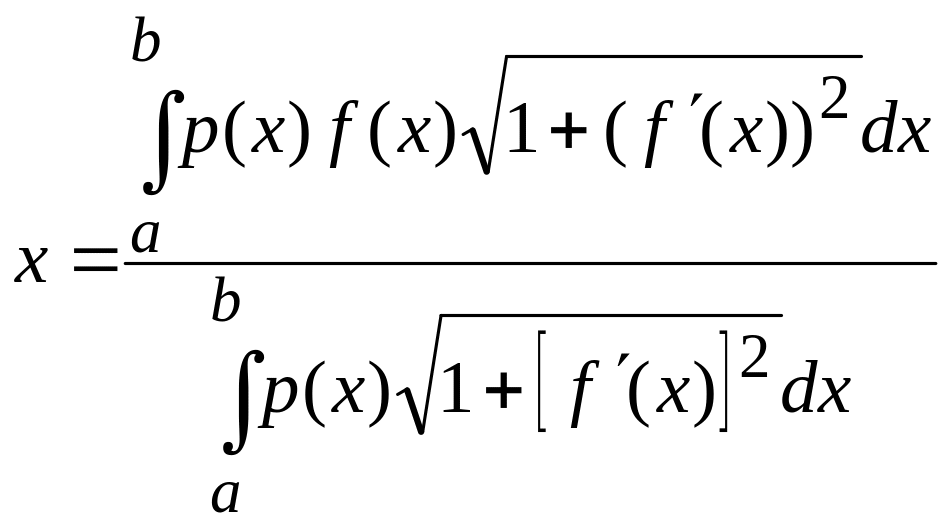
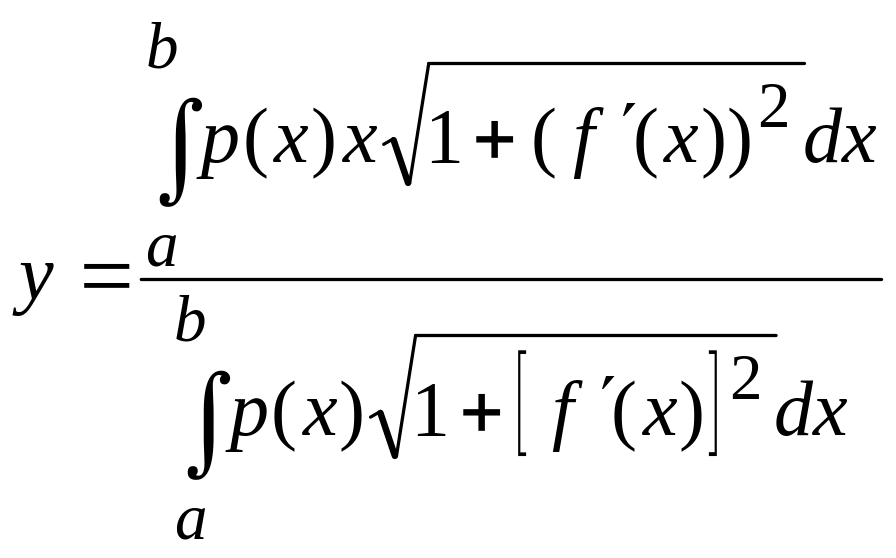
№25Приближенное вычисление
определенного интеграла
В
некоторых случаях не удается точно
найти значение определенного
интеграла(Определение.
Если существует конечный предел
интегральных при уменьшении длин
отрезков разбиения, то он не зависит
от способов разбиения отрезка. Этот
предел называется определенным
интегралом от функции f(x)
по отрезку [a,b]
и обозначается
 .
.
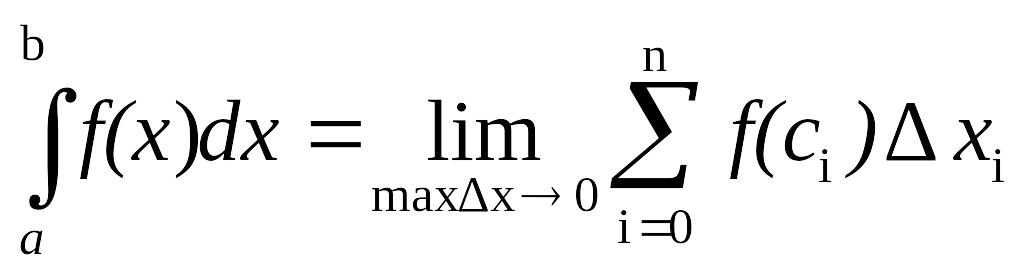 .
.
). Тогда его вычисляют приближенно.
Пусть функция y = f(x) определена и непрерывна на [a,b].
 Y
Y
y=f(x)
0 а=х0 х1 х2 х n-1 х n=b X
Разобьем
отрезок на n
равных частей точками a
= x0<
x1
<
x2
<
<
….<
xn
= b. Обозначим
длину отрезка разбиения -
![]() .
.
Мы получаем фигуру, ограниченную ломаной линией, которая с ростом n будет все точнее давать значения площади S криволинейной трапеции. Найдем площадь этой фигуры.
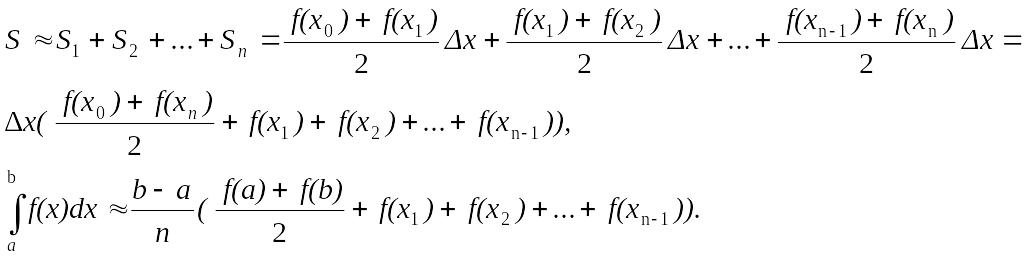
Мы получили формулу трапеций для приближенного вычисления интеграла.
Абсолютная
погрешность:
![]()
Билет №26
Несобственные интегралы с бесконечными пределами
![]()
Опр.:
Если существует
предел при
![]() от интеграла от a
до R
f(x)dx,
то существует интеграл от a
до
от интеграла от a
до R
f(x)dx,
то существует интеграл от a
до
![]() f(x)dx
– несобственный интеграл 1 рода.
f(x)dx
– несобственный интеграл 1 рода.
Если существует конечный предел интеграла при , то несобственный интеграл сходится
Если предел расходится, то несобственный интеграл тоже расходится.
Геометрический смысл:
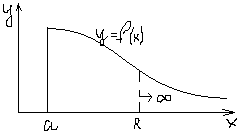
![]() бесконечной
фигуры под y=f(x)
бесконечной
фигуры под y=f(x)
-сходится
Аналогично
![]()
Существует,
если существует
![]()

Аналогично:
![]() или
или
![]()

Билет № 27
Определение дифференциального уравнения первого порядка. Существование решения дифференциального уравнения.
Функция
y=f(x)
называется дифференцируемой в точке
x0,
если ее приращение
![]() может
быть представлено в виде
может
быть представлено в виде
![]()
Главная
линейная часть
![]() приращения
приращения
![]() называется дифференциалом этой функции
в точке x0,
соответствующим приращению
называется дифференциалом этой функции
в точке x0,
соответствующим приращению
![]() ,
и обозначается символом dy(x0,
).
,
и обозначается символом dy(x0,
).
Для того чтобы функция y=f(x) была дифференцируемой в точке x0, необходимо и достаточно, чтобы существовала производная f `(x); при этом справедливо равенство A=f ` (x0).
Это утверждение позволяет называть дифференцируемость всякую функция, имеющую производную. Выражение для дифференциала имеет вид dy(x0,dx)=f `(x0)dx,
Где
принято обозначение dx=
.
Из формулы
следует, что если f
`(x0)![]() 0,
то при
->0
приращение функции и ее дифференциал
dy
в фиксированной точке являются
эквивалентными бесконечно малыми, что
позволяет записать приближенное
равенство:
0,
то при
->0
приращение функции и ее дифференциал
dy
в фиксированной точке являются
эквивалентными бесконечно малыми, что
позволяет записать приближенное
равенство:
![]() при |
|<<1
при |
|<<1
Билет №28
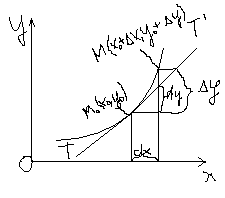
Геометрический смысл дифференциального уравнения первого порядка
Геометрический смысл дифференциала: Дифференциал dy(x0, ) равен приращению ординаты касательной TT` к графику функции y=f(x) в точке М0(x0,y0) при приращении аргумента, равном
Билет №29 Дифференциальные уравнения с разделяющимися переменными
Дифференциальными уравнениями с разделяющимися переменными называют уравнения вида
X1(x) Y1(y)dx + X2(x) Y2(y)dy = 0.
Перенесем второе слагаемое в правую часть.
X1(x) Y1(y)dx = -X2(x) Y2(y)dy .
Предположим, что Y1(y) X2(x) ¹ 0. Разделим обе части уравнения на это произведение:
![]() .
.
Переменные разделились. Интегрируя обе части этого равенства, получим общее решение уравнения(Определение. Решение дифференциального уравнения n-го порядка, содержащее n произвольных постоянных, называется общим решением дифференциального уравнения.):
![]() .
.
Пример.
![]() .
.
dy
= y' dx, y' =
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
y,
x
>0.
,
y,
x
>0.
![]() ,
,
![]() ,
,
![]() ,
,
y=c1 x.
Билет №30 Линейные дифференциальные уравнения первого порядка
Линейное дифференциальное уравнение(Определение 1. Уравнение, содержащее независимую переменную, функцию от этой независимой переменной и ее производные различных порядков, называется дифференциальным уравнением.
Определение 2. Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.
Дифференциальное уравнение n-го порядка имеет вид
F(x,y,y',y'', …, y(n))=0.
) первого порядка имеет вид
a (x) y' + b (x) y + c(x) = 0, (1)
 a
(x)
a
(x)
![]() 0
.
0
.
Разделим обе части уравнения на a(x).
y'
+ p(x) y + q(x) = 0,
где
p(x) = ![]() , q(x)
=
, q(x)
=
![]() . (2)
. (2)
Будем искать решения уравнения(Определение. Решением дифференциального уравнения называется любая функция y = j(x), при подстановке которой в уравнение будет получено тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения, график решения называют интегральной кривой.
) (2) в виде произведения двух неизвестных функций:
y = u · v.
Подставим y = u · v · в (2)
![]() ,
,
![]() . (3)
. (3)
Выберем
функцию u
так, чтобы
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Подставим полученную функцию u(х) в (3) и найдем n(х):
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Подставим функции u(х) и n(х) в выражение для у:
![]() -
общее решение(Определение.
Решение дифференциального уравнения
n-го
порядка, содержащее n
произвольных постоянных, называется
общим решением дифференциального
уравнения.
-
общее решение(Определение.
Решение дифференциального уравнения
n-го
порядка, содержащее n
произвольных постоянных, называется
общим решением дифференциального
уравнения.
) линейного дифференциального уравнения первого порядка.
Пример.
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
u=x.
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
Билет 31.
Линейные дифференциальные уравнения первого порядка.
Уравнение
вида
![]() называется
линейным неоднородным уравнением.
Уравнение вида
называется
линейным неоднородным уравнением.
Уравнение вида
![]() называется
линейным однородным уравнением.
называется
линейным однородным уравнением.
Очевидно,
что однородное линейное уравнение
является уравнением с разделяющимися
переменными и его общее решение
вычисляется по формуле
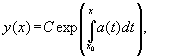 где
C—
произвольная
постоянная,
где
C—
произвольная
постоянная,
Общее решение линейного однородного уравнения первого порядка.
y(x0)
=
y0
определяется
выражением
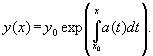
Метод
вариации произвольных постоянных для
линейного неоднородного уравненя
состоит в том, что решение неоднородного
уравнения записывается в виде
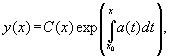
 где
C(x)
неизвестная функция. Подставляя в
уравнение имеем для C(x)
откуда
где
C(x)
неизвестная функция. Подставляя в
уравнение имеем для C(x)
откуда
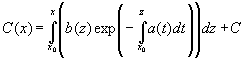 и
тогда для общего решения неоднородного
уравнения справедливо
и
тогда для общего решения неоднородного
уравнения справедливо
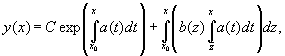 где
C
— произвольная
постоянная.
где
C
— произвольная
постоянная.
Для
решения задачи Коши y(x0)
=
y0
для
линейного неоднородного уравнения
справедлива формула
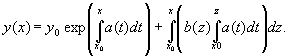
Метод вариации производной постоянной при решении линейного диф. уравнения 1-го порядка.
y’+P(x)y=Q(x) (1) -задано линейное неоднородное уравнение. Рассмотрим соотв. ему однородное уравнение y’=P(x)y=0 (2). Найдём общее решение:
![]()
![]()
![]()
![]()
Будем
искать решение в том же виде, что и
однородного, только считая с
не произвольной константой ,а функцией
от х :
![]()
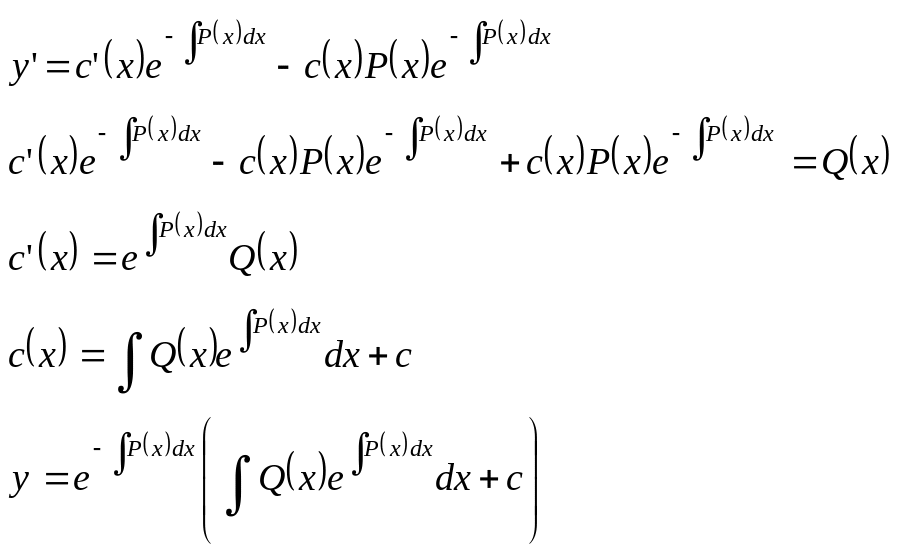
Билет 32.
Уравнение Бернулли
Уравнение Бернулли – это диф. Ур-е следующего вида :
![]()
где P(x) и Q(x) – непрерывные функции m – действительное число 0 и 1
разделим уравнение на ym :
![]() -
приведем его к линейному
-
приведем его к линейному
Обозначим
через
![]() а теперь диференциируем
а теперь диференциируем
![]()
теперь подставим в уравнение
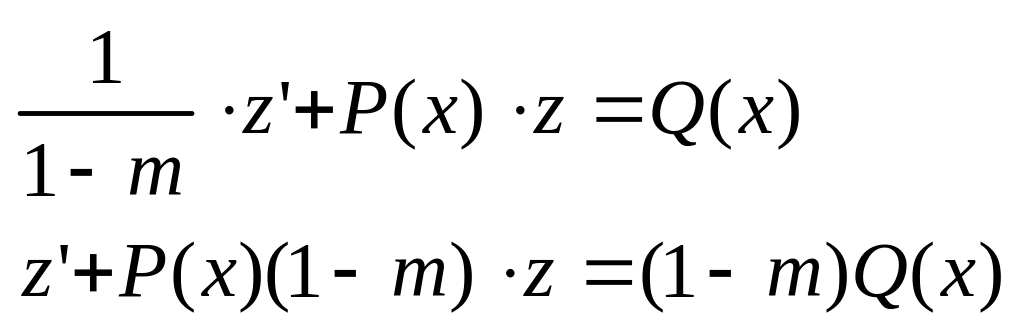
получили линейное уравнение .
Билет 33.
Уравнение в полных дифференциалах. Интегрирующий множитель.
Обыкновенное дифференциальное уравнение первого порядка вида P(x, y) dx + Q(x, y) dy = 0 называется уравнением в полных дифференциалах, если P(x, y) и Q(x, y) непрерывны в некоторой односвязной области D и в этой области выполнено условие
![]()
Тогда
общий
интеграл
уравнения задается выражением
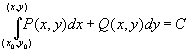 .
.
Обозначим
![]() тогда
тогда
![]() откуда
откуда
![]() и
формула для вычисления u(x,
y)
имеет вид:
и
формула для вычисления u(x,
y)
имеет вид:
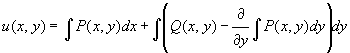
Выражение u(x, y)=0, где
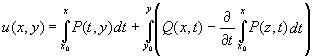
задает решение задачи Коши y(x0) = y0.
Уравнение в полных дифференциалах и их решение
Пусть задано диф. ур-е ел. Вида:
![]()
где P(x,y) и Q(x,y) – непрер. Функции имеющие непрерыв часн. Производную 2 порядка включительно.
Диф.
ур. Назыв. Ур-ем в полных диф-лах , если
![]() такое что
такое что
![]()
т.е.
ур. В этом случае имеет вид :![]()
это уравнение явл полным диф. функции U как ф-ции двух переменных:
![]()
если
выполняется равенство тогда то левая
часть
![]() а тогда его решение
а тогда его решение
![]() -
общий интеграл диф. Ур.
-
общий интеграл диф. Ур.
Теорема о необходимости и достаточности условия того что Ур было ур-ем в полных дифференциалах
Теорема : Для того чтобы ур было ур-ем в полных диф. в некоторой Д принадл ХОУ
Необх.
И дост. Чтобы во всех точках обл. Д выполн
равенство
![]() если условие выполняется можно найти
ф-цию
если условие выполняется можно найти
ф-цию
![]() что будет выполняться рав-во след.
Образом.
что будет выполняться рав-во след.
Образом.
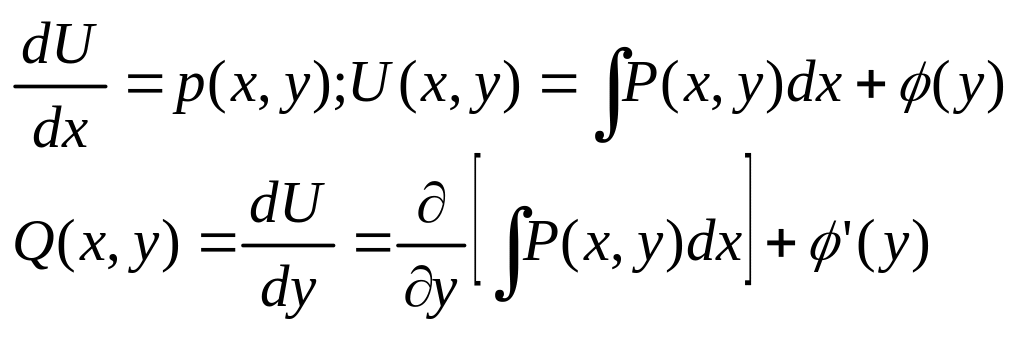
найдем
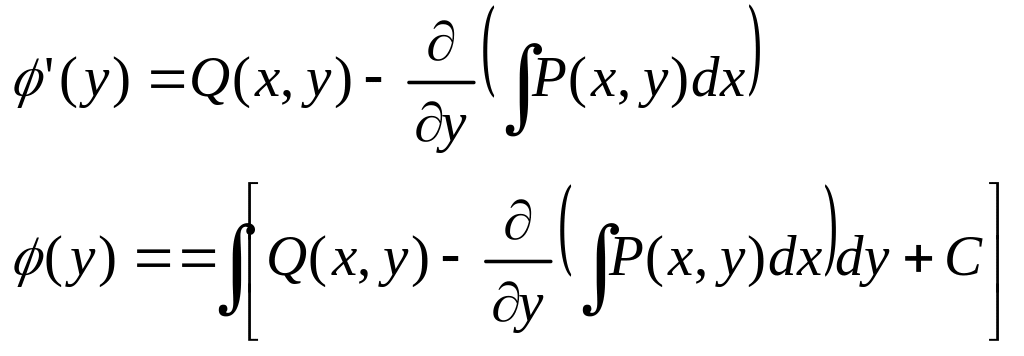
Интегральный множитель и его нахождение
Пусть задано диф. ур-ние в диф. форме вида :
![]()
не
всякое такое уравнение явл. Уравнением
в полных виференциалах однако доказано
что для всякого такого ур-я может быть
подобрана ф-ция
![]() такая
что после умножения левого и правого
ур-я на эту функцию данное уравнение
стан ур-ем в полных диф. Ф-цияю
назыв
интегральным множителем данного
уравнения
такая
что после умножения левого и правого
ур-я на эту функцию данное уравнение
стан ур-ем в полных диф. Ф-цияю
назыв
интегральным множителем данного
уравнения
Найдем функцию определяющую интегр. Множитель данного уравнения:
![]()
тогда должно выполн. Рав-во:

имеем уравнение в частных производных относит неизв функции Мю.Общего метода нахожения которой не существует
Найдем интегр множитель в случае если он явл ф-цией от одной из перемен.
1)Найдем
условие при которых
![]() функция
функция
![]() должна
удовлетв равенству
должна
удовлетв равенству
![]() ;
;![]() будет
зависеть только от Х если правая часть
ур будет зависеть только от Х
будет
зависеть только от Х если правая часть
ур будет зависеть только от Х
2) Аналогично и = (У)
![]() ;
будет
зависеть только от Х если правая часть
ур будет зависеть только от
;
будет
зависеть только от Х если правая часть
ур будет зависеть только от
y
Билет 34.
Дифференциальные уравнения порядка выше 1-го, допускающие понижения порядка.
А)Уравнения
вида
![]() .Общее
решение получается путём n-кратного
интегрирования
.Общее
решение получается путём n-кратного
интегрирования
![]() ,где
,где
![]() ,
или по формуле
,
или по формуле
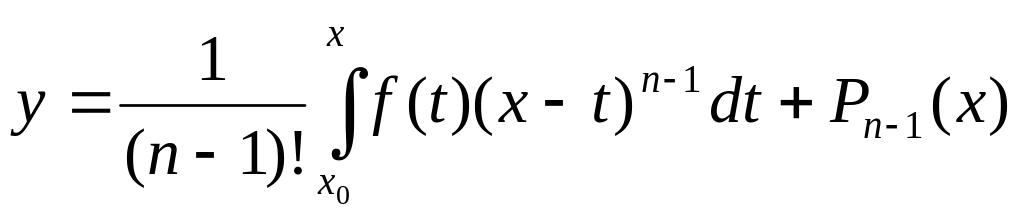
б)
![]() ,
т.е. уравнения не содержащие явно искомой
функции и её производных до порядка
(k-1)
включительно.С помощью замены переменной
,
т.е. уравнения не содержащие явно искомой
функции и её производных до порядка
(k-1)
включительно.С помощью замены переменной
![]() порядок
уравнения понижается на k
единиц:
порядок
уравнения понижается на k
единиц:
![]() .Предположим , что для полученного
уравнения путём N-кратного
интегрирования мы можем найти общее
решение
.Предположим , что для полученного
уравнения путём N-кратного
интегрирования мы можем найти общее
решение
![]() .Тогда
искомая функция y(x)
получается путём k-кратного
интегрирования функции
.Тогда
искомая функция y(x)
получается путём k-кратного
интегрирования функции
![]() .
.
в)
![]() ,
не содержащие явно зависимой переменной.
Подстановкой
,
не содержащие явно зависимой переменной.
Подстановкой
![]() ,
и т.д. порядок уравнения понижается на
единицу.
,
и т.д. порядок уравнения понижается на
единицу.
г)
![]() ,
т.е. такие уравнения , в которых левая
часть может быть представлена как
полная производная по x
от некоторой функции
,
т.е. такие уравнения , в которых левая
часть может быть представлена как
полная производная по x
от некоторой функции
![]() ,.Интегрируя
по х , получим новое уравнение, порядок
которого на 1 ниже порядка исходного
уравнения.
,.Интегрируя
по х , получим новое уравнение, порядок
которого на 1 ниже порядка исходного
уравнения.
д)
![]() ,
однородное относительно функции и её
производных, т.е. такое, что
,
однородное относительно функции и её
производных, т.е. такое, что
![]() .Подстановкой
.Подстановкой
![]() порядок уравнения понижается на 1.
порядок уравнения понижается на 1.
Билет 35.
Линейные неоднородные дифференциальные уравнения порядка выше 1-го
Вид:
![]() ,в
котором f(x)
,в
котором f(x)![]() ,называетсялинейным
неоднородным ДУ n-го
порядка.Общее решение уравнения (1)
определяется формулой
,называетсялинейным
неоднородным ДУ n-го
порядка.Общее решение уравнения (1)
определяется формулой![]() ,
где
,
где
![]() -общее
решение соответствующего однородного
уравнения, а
-общее
решение соответствующего однородного
уравнения, а
![]() -некоторое
частное решение неоднородного
уравнения(1).
-некоторое
частное решение неоднородного
уравнения(1).
Если
известно общее решение
![]() ,
соответствующего уравнению (1) однородного
уравнения , то для определения частного
решения
уравнения
(1) используют метод Лагранжа вариации
произвольных постоянных.Именно , ищут
частное решение неоднородного уравнения
(1) в виде
,
соответствующего уравнению (1) однородного
уравнения , то для определения частного
решения
уравнения
(1) используют метод Лагранжа вариации
произвольных постоянных.Именно , ищут
частное решение неоднородного уравнения
(1) в виде
![]() ,
где от функций
,
где от функций
![]() дополнительно требуется,чтобы они
удовлетворяли условиям
дополнительно требуется,чтобы они
удовлетворяли условиям
![]() для всех
для всех![]() (где
(где
![]() .Тогда
дляфункций
.Тогда
дляфункций![]() ,получимсистемууравнений
,получимсистемууравнений
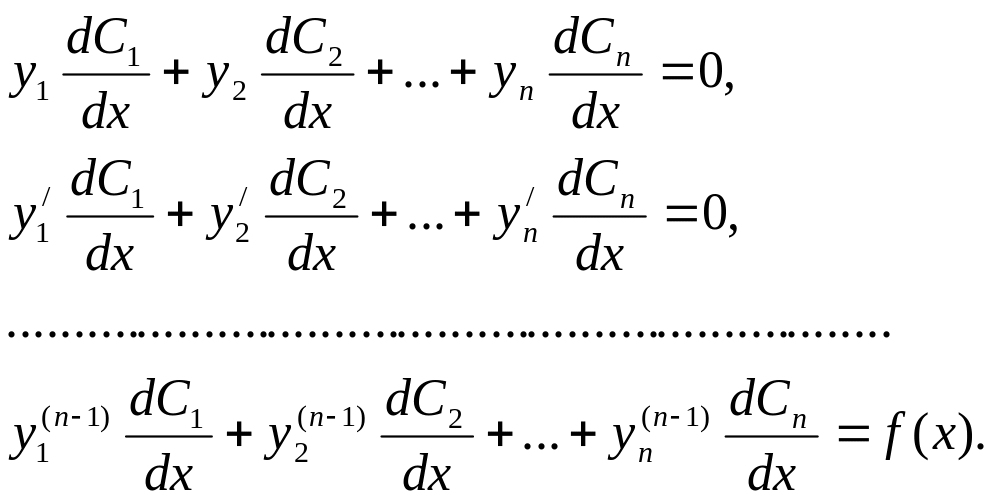
Определитель
этой системы есть отличный от нуля
вронскиан фундаментальной системы
решений
![]() ,поэтому
система имеет единственное решение
относительно
,поэтому
система имеет единственное решение
относительно
![]()
Билет 36
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Билет 37
Линейные однородные дифференциальные уравнения порядка выше 1-го с постоянными коэффициентами
Линейные однородные дифференциальные уравнения порядка выше 1-го с постоянными коэффициентами.
![]() ,
где
,
где
![]() -действительные
постоянные.(1)
-действительные
постоянные.(1)
Уравнение
![]() (2),полученное
заменой производных
(2),полученное
заменой производных
![]() искомой
функцией степенями
искомой
функцией степенями
![]() ,
называется характеристическим уравнением
,
называется характеристическим уравнением
уравнения
(2).Каждому
действительному корню
![]() уравнения
(2) кратностиr
соответствуют r
линейно независимых решений уравнения(1):
уравнения
(2) кратностиr
соответствуют r
линейно независимых решений уравнения(1):
![]() ,
а каждой паре комплексных корней
,
а каждой паре комплексных корней
![]() ,
кратности s
соответствуют s
пар линейно независимых решений :
,
кратности s
соответствуют s
пар линейно независимых решений :
![]()
Если
характеристическое уравнение имеет k
действительных корней
![]() кратностей
кратностей
![]() и
l
пар комплексно сопряжённых корней
и
l
пар комплексно сопряжённых корней
![]() кратностей
кратностей
![]() ,
то общее решение уравнения (1) запишется
в виде
,
то общее решение уравнения (1) запишется
в виде
![]() где
где
![]() -произвольный
многочлен степени
-произвольный
многочлен степени
![]() ,
а
,
а
![]() и
и
![]() -произвольные
многочлены степени
-произвольные
многочлены степени
![]()
Для
линейного однородного дифференциального
уравнения с
постоянными коэффициентами
существует простой алгоритм построения
фундаментальной системы решений. Будем
искать решение уравнения в виде y(x)
=
![]() =
=![]()
exp(lx)(n) + a1exp(lx)(n-1) + ... + an-1exp(lx)' + anexp(lx)= = (ln + a1ln-1 + ... + an-1l + an)exp(lx) = 0, т.е. число l является корнем характеристического уравнения ln + a1ln-1 + ... + an-1l + an = 0. Левая часть характеристического уравнения называется характеристическим многочленом линейного дифференциального уравнения: P(l) = ln + a1ln-1 + ... + an-1l + an. Таким образом, задача о решении линейного однородного уравнения n -го порядка с постоянными коэффициентами сводится к решению алгебраического уравнения.
Если характеристическое уравнение имеет n различных действительных корней l1№ l2 № ... № ln, то фундаментальная система решений состоит из функций y1(x) = exp(l1x), y2(x) = exp(l2x), ..., yn(x) = exp(lnx), и общее решение однородного уравнения имеет вид: y(x)= c1 exp(l1x) + c2 exp(l2x) + ... + cn exp(lnx).
Если какой-либо из действительных корней характеристического уравнения повторяется r раз (r-кратный корень), то в фундаментальной системе решений ему отвечают r функций; если lk=lk+1 = ... = lk+r-1, то в фундаментальную систему решений уравнения входят r функций: yk(x) = exp(lkx), yk+1(x) = xexp(lkx), yk+2(x) = x2exp(lkx), ..., yk+r-1(x) =xr-1 exp(lnx).
Если характеристическое уравнение имеет комплексные корни, то каждой паре простых (имеющих кратность 1 ) комплексных корней lk,k+1=ak ± ibk в фундаментальной системе решений отвечает пара функций yk(x) = exp(akx)cos(bkx), yk+1(x) = exp(akx)sin(bkx).
Если же комплексная пара корней имеет кратность r, то такой паре lk=lk+1 = ... = l2k+2r-1=ak ± ibk, в фундаментальной системе решений отвечают функции exp(akx)cos(bkx), exp(akx)sin(bkx), xexp(akx)cos(bkx), xexp(akx)sin(bkx), x2exp(akx)cos(bkx), x2exp(akx)sin(bkx), ................ xr-1exp(akx)cos(bkx), xr-1exp(akx)sin(bkx).
Таким образом, для отыскания общего решения линейного однородного дифференциального уравнения с постоянными коэффициентами следует: записать характеристическое уравнение; найти все корни характеристического уравнения l1, l2, ... , ln; записать фундаментальную систему решений y1(x), y2(x), ..., yn(x); записать выражение для общего решения y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x).
Билет38
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод вариации постоянных
Билет 39
Линейные неоднородные дифференциальные уравнения порядка выше 1-го с постоянными коэффициентами. Метод вариации постоянных
Для линейного неоднородного дифференциального уравнения n-го порядка
y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = f(x),
где y = y(x) — неизвестная функция, a1(x), a2(x), ..., an-1(x), an(x), f(x) — известные, непрерывные, справедливо: 1) если y1(x) и y2(x) — два решения неоднородного уравнения, то функция y(x) = y1(x) - y2(x) — решение соответствующего однородного уравнения; 2) если y1(x) решение неоднородного уравнения, а y2(x) — решение соответствующего однородного уравнения, то функция y(x) = y1(x) + y2(x) — решение неоднородного уравнения; 3) если y1(x), y2(x), ..., yn(x) — n линейно независимых решений однородного уравнения, а yч(x) — произвольное решение неоднородного уравнения, то для любых начальных значений x0, y0, y0,1, ..., y0,n-1 существуют такие значения c*1, c*n, ..., c*n, что решение y*(x)=c*1 y1(x) + c*2 y2(x) + ... + c*n yn (x) + yч(x) удовлетворяет при x = x0 начальным условиям y*(x0)=y0, (y*)'(x0)=y0,1 , ...,(y*)(n-1)(x0)=y0,n-1.
Выражение y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) + yч(x) называется общим решением линейного неоднородного дифференциального уравнения n-го порядка.
Для отыскания частных решений неоднородных дифференциальных уравнений с постоянными коэффициентами с правыми частями вида: Pk(x)exp(ax)cos(bx) + Qm(x)exp(ax)sin(bx), где Pk(x), Qm(x) — многочлены степени k и m соответственно, существует простой алгоритм построения частного решения, называемый методом подбора.
Метод подбора, или метод неопределенных коэффициентов, состоит в следующем. Искомое решение уравнения записывается в виде: (Pr(x)exp(ax)cos(bx) + Qr(x)exp(ax)sin(bx))xs, где Pr(x), Qr(x) — многочлены степени r = max(k, m) с неизвестными коэффициентами pr , pr-1, ..., p1, p0, qr, qr-1, ..., q1, q0. Сомножитель xs называют резонансным сомножителем. Резонанс имеет место в случаях, когда среди корней характеристического уравнения есть корень λ =a ± ib кратности s. Т.е. если среди корней характеристического уравнения соответствующего однородного уравнения есть такой, что его действительная часть совпадает с коэффициентом в показателе степени экспоненты, а мнимая — с коэффициентом в аргументе тригонометрической функции в правой части уравнения, и кратность этого корня s, то в искомом частном решении присутствует резонансный сомножитель xs. Если же такого совпадения нет (s=0), то резонансный сомножитель отсутствует.
Подставив выражение для частного решения в левую часть уравнения, получим обобщенный многочлен того же вида, что и многочлен в правой части уравнения, коэффициенты которого неизвестны. Два обобщенных многочлена равны тогда и только тогда, когда равны коэффициенты при сомножителях вида xtexp(ax)sin(bx), xtexp(ax)cos(bx) с одинаковыми степенями t. Приравняв коэффициенты при таких сомножителях, получим систему 2(r+1) линейных алгебраических уравнений относительно 2(r+1) неизвестных. Можно показать, что такая система совместна и имеет единственное решение.
Таким образом, для отыскания общего решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует найти общее решение соответствующего однородного уравнения (записать характеристическое уравнение, найти все корни характеристического уравнения λ1,λ2, ... , λn, записать фундаментальную систему решений y1(x), y2(x), ..., yn(x)); найти любое частное решение неоднородного уравнения yч(x); записать выражение для общего решения y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) + yч(x);
Билет 39.
Линейные неоднородные дифференциальные уравнения порядка выше 1-го с постоянными коэффициентами. Метод вариации постоянных
Доказано, что для линейного неоднородного дифференциального уравнения y(n) + a1 y(n-1) + ... + an-1 y' + an y = f(x) при непрерывной правой части f(x), для любых начальных значений x0, y0, y0,1, ..., y0,n-1 существует и единственно решение задачи Коши y(x0)=y0, (y)'(x0)=y0,1 , ...,(y)(n-1)(x0)=y0,n-1.
Решение задачи Коши для неоднородного дифференциального уравнения с постоянными коэффициентами можно найти методом вариации произвольных постоянных (методом Лагранжа), который состоит в следующем: Записываем искомое решение задачи Коши для неоднородного уравнения в виде y(x)= c1(x) y1(x) + c2(x) y2(x) + ... + cn(x) yn(x), где y1(x), y2(x), ..., yn(x) — линейно независимые решения соответствующего однородного уравнения, и находим неизвестные функции c1(x) , c2(x), ..., cn(x), такие, чтобы функция y = y(x) удовлетворяла неоднородному уравнению и заданным начальным условиям.
Опишем алгоритм решения задачи Коши для уравнения второго порядка y'' + a1 y' + a2 y = f(x), y(x0)=y0, (y)'(x0)=y0,1. Будем искать решение задачи в виде y(x)= c1(x) y1(x) + c2(x) y2(x), где y1(x), y2(x) — линейно независимые решения однородного уравнения y'' + a1 y' + a2 y = 0. Вычислим y'(x), y''(x) и подставим полученные выражения в уравнение. Вычислим первую производную y'(x)= (c1'(x) y1(x) + c2(x)' y2(x)) + (c1(x) y1'(x) + c2(x) y2'(x)), положим c1'(x) y1(x) + c2(x)' y2(x) = 0 и тогда y'(x)= c1(x) y1'(x) + c2(x) y2'(x), y''(x)= (y'(x))'= (c1(x) y1'(x) + c2(x) y2'(x))'= =c1'(x) y1'(x) + c2(x)' y2'(x) + c1(x) y1''(x) + c2(x) y2''(x).
Подставив y(x) и ее производные в уравнение, получим: y'' + a1 y' + a2 y = = c1'(x) y1'(x) + c2(x)' y2'(x) + c1(x) y1''(x) + c2(x) y2''(x) + + a1(c1(x) y1'(x)+c2(x) y2'(x)) + a2(c1(x) y1(x)+c2(x) y2(x)) = = c1(x)( y1''(x)+a1 y1'(x)+a2 y1(x)) + c2(x)( y2''(x)+a1 y2'(x)+a2 y2(x)) + + c1'(x) y1'(x) + c2(x)' y2'(x) = 0 + 0 + c1'(x) y1'(x) + c2(x)' y2'(x) = f(x), при условии c1'(x) y1(x) + c2(x)' y2(x) = 0.
Тогда
неизвестные функции c1(x)
и c2(x)
являются решениями системы линейных
дифференциальных уравнений
c1'(x)
y1'(x)
+ c2(x)'
y2'(x)
= f(x),
c1'(x)
y1(x)
+ c2(x)'
y2(x)
= 0
с известными y1(x)
и y2(x).
Эта
система легко разрешима относительно
c1(x)
и c2(x):
c1'(x)
= f(x)y2(x)/(y1'(x)y2(x)-y1(x)y2'(x)),
c1'(x)=
f(x)y1(x)/(y1(x)y2'(x)-y1'(x)y2(x)).
Вычислив
интегралы в правой части системы,
получим
![]()
![]()
Произвольные константы C1 и C2 определяются из начальных условий.
Заметим, что разрешимость системы дифференциальных уравнений для c1'(x) и c2'(x) и однозначная разрешимость системы начальных условий для произвольных констант C1 и C2 гарантированы линейной независимостью y1(x) и y2(x), (y1'(x)y2(x)-y1(x)y2'(x))№0 для линейно независимых y1(x) и y2(x).
Для того чтобы решить задачу Коши для уравнения более высокого порядка действуем аналогично. Решение задачи Коши ищем в виде y(x)= c1(x) y1(x) + c2(x) y2(x) + ... + cn(x) yn(x), где y1(x), y2(x), ..., yn(x) — линейно независимые решения соответствующего однородного уравнения. Неизвестные функции c1(x) , c2(x), ..., cn(x) находим как решения линейной системы дифференциальных уравнений c1'(x) y1(x) + c2(x)' y2(x) + ... + cn'(x) yn(x) = 0 c1'(x) y1'(x) + c2'(x) y2'(x) + ... + cn'(x) yn'(x) = 0, c1'(x) y1''(x) + c2'(x) y2''(x) + ... + cn'(x) yn''(x) = 0, ................. c1'(x) y1(n-1)(x) + c2'(x) y2(n-1)(x) + ... + cn'(x) yn(n-1)(x) = f(x), которая в силу линейной независимости y1(x), y2(x), ..., yn(x) разрешима относительно ci'(x). Вычислив ci(x) = Fi(x) + Ci находим произвольные постоянные Ci из начальных условий и тогда искомое решение уравнения имеет вид y(x)= F1(x) y1(x) + F2(x) y2(x) + ...+ Fn(x) yn(x) + C1y1(x) + C2 y2(x) +...+ Cnyn(x).
Таким образом, для того чтобы решить методом вариации произвольных постоянных решение задачи Коши для линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует: записать характеристическое уравнение; найти все корни характеристического уравнения λ1,λ 2, ... , λn; найти фундаментальную систему решений y1(x), y2(x), ..., yn(x)); представить искомое решение задачи Коши в виде линейной комбинации y(x)= c1(x)y1(x) + c2(x)y2(x) + ... + cn(x)yn(x), с неизвестными функциями c1(x), c2(x), ..., cn(x); составить и решить систему для c1 (x), c2(x), ..., cn(x); подставить вычисленные ci(x) = Fi(x) + Ci в выражение для решения и записать для него начальные условия; найти из начальных условий значения констант Ci и записать искомое решение.
Для отыскания общего решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует найти общее решение соответствующего однородного уравнения (записать характеристическое уравнение, найти все корни характеристического уравнения λ1,λ2, ... , λn, записать фундаментальную систему решений y1(x), y2(x), ..., yn(x)); найти методом вариации произвольных постоянных любое частное решение неоднородного уравнения yч(x); записать выражение для общего решения y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) + yч(x).
Если известно общее решение , соответствующего уравнению (1) однородного уравнения , то для определения частного решения уравнения (1) используют метод Лагранжа вариации произвольных постоянных.Именно , ищут частное решение неоднородного уравнения (1) в виде , где от функций дополнительно требуется,чтобы они удовлетворяли условиям для всех (где .Тогда дляфункций ,получимсистемууравнений
Определитель этой системы есть отличный от нуля вронскиан фундаментальной системы решений ,поэтому система имеет единственное решение относительно
Билет 40. Линейные дифференциальные уравнения порядка выше 1-го с постоянными коэффициентами и специальной правой частью.
![]()
а)
![]() ,
где
,
где
![]() методом неопределённых коэффициентов.
методом неопределённых коэффициентов.
Б)
![]()
Если λ несовпадает с корнями характеристического уравнения.
В)Если λ совпадает с корнями хар-го уравнения .
s-степень кратности
![]()
г
)
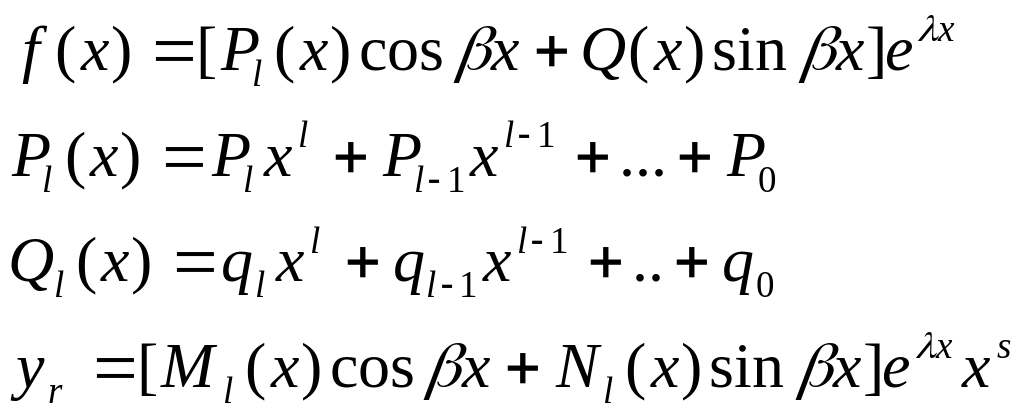
s- степень кратности.
Теорема:Если
![]() -решение
уравнения
-решение
уравнения
![]()
Если
![]() -решение
уравнения
-решение
уравнения
![]() .
.
Тогда
y=
![]() -будет
решением уравнения
-будет
решением уравнения
![]() .
.
Док-во:
y=![]() .
.
![]()
![]()
![]() -
-
Принцип суперпозиции.
Билет 41. . Основные понятия функции нескольких переменных
Если каждой паре (x,y) значений двух, независимых друг от друга , переменных величин x и y , из некоторой области их изменения D соответствует определённое значение величины z , то мы говорим, что z есть функция двух независимых переменных x и y, определённая в области D.
Обозначение:z=f(x,y), z=F(x,y) и т.д.
Совокупность пар (x,y) значений x и y , при которых определяется функция z=f(x,y), называется областью определения этой функции.
Область определения наглядно иллюстрируется геометрически. Если каждую пару значений x ,y мы будем изображать точкой M(x,y) в плоскости Oxy,то область определения функции изобразится в виде некоторой совокупности точек на плоскости.Эту совокупность называют также областью определения. Линию , ограничивающую данную область называют границей области. Точки, не лежащие на границе- внутренние.
Область, состоящая из одних внутренних точек –открытая или незамкнутая. Если к области относятся и точки границы , то область замкнутая.
Область называется ограниченной, если существует такое постоянное C, что расстояние до любой точки M области от начала координат O меньше С, т.е. |OM|<C.
Функция нескольких переменных может быть задана с помощью таблицы или формулы.
