1. Определение производной. Ее физический смысл. Определение дифференцируемой функции. Сформулировать теорему о связи между дифференцируемостью и непрерывностью функции.

Производная — основное понятие дифференциального исчесления, характеризующее скорость изменения функции.

Производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Функцию, имеющую конечную производную, называют дифференцируемой.  Процесс вычисления производной называется дифференцированием

Если положение точки при её движении по числовой  прямой задаётся функцией S= f(t), где t – время движения, то производная функции S – мгновенная скорость движения в момент времени t. По аналогии с этой моделью вообще говорят о том, что производная функции у = f(x) – скорость изменения функции в точке х.

Теорема (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке, то она непрерывна в этой точке.

Доказательство. Пусть функция у=f(x) дифференцируема в точке х₀. Дадим в этой точке аргументу приращение х. Функция получит приращение у. Найдем  .

.

Следовательно, у=f(x) непрерывна в точке х₀.

Следствие. Если х₀ – точка разрыва функции, то в ней функция не дифференцируема.

Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.

Пример. у=|х| , х₀=0.

 

            

х>0,              ;

х<0,              .

В точке х₀=0 функция непрерывна, но производной не существует.

2. Геометрический смысл производной. Уравнения касательной и нормали

Геометрический смысл производной.  Рассмотрим график функции  y = f ( x ): 

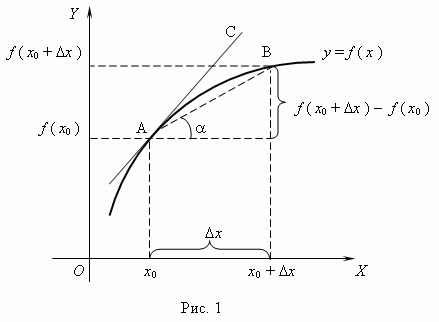
Из рис.1  видно, что для любых двух точек A и B графика функции:  

где    - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точкуB, то    неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x₀ ,  f ( x₀  ) ). В общем случае уравнение прямой с угловым коэффициентом  f ’( x₀ )  имеет вид: 

y = f ’( x₀ ) · x + b .

Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:

f ( x₀ ) = f ’( x₀ ) · x₀ + b ,

отсюда,  b =  f ( x₀ ) – f ’( x₀ ) · x₀ , и подставляя это выражение вместо  b, мы получим  уравнение касательной:

y =  f ( x₀ ) +  f ’( x₀ ) · ( x – x₀  ) .

Нормалью к графику функции y = f (x) в точке A (x₀; y₀) называется прямая, проходящая через точку A и перпендикулярная касательной к этой точке. Она задается уравнением 

что следует из свойства угловых коэффициентов перпендикулярных друг другу прямых.

В случае бесконечной производной   касательная в точке x₀ становится вертикальной и задается уравнением x = x₀, а нормаль – горизонтальной: y = y₀.