15. Определения возрастающей, убывающей, монотонной функции. Сформулировать необходимое условие монотонности функции. Достаточное условие монотонности функции.

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Функция F возрастает на интервале (а;в) если для любых Х1 и Х2 из этого интервала, таких, что Х1 больше Х2, выполняется неравенство F(Х1) больше F (Х2).  Убывает - если F(Х1) меньше F (Х2).

Достаточные условия строгой монотонности функции на интервале:

Теорема 22.1. Для того чтобы дифференцируемая на интервале (a;b) функция   возрастала (убывала) на этом интервале достаточно, чтобы производная   была положительной (отрицательной) всюду на этом интервале.

Теорема 22.2. Для того чтобы дифференцируемая на интервале (a;b) функция    не убывала (не возрастала) на этом интервале, необходимо и достаточно, чтобы производная этой функции была неотрицательной (неположительной) всюду на этом интервале.

Положительность (отрицательность) производной  f '(x)  на Х не является необходимым условием возрастания (убывания) функции f(x), т.е. если на некотором участке функция возрастае (убывает), то отсюда не следует, вообще говоря, что на этом участке производная этой функции всюду положительна (отрицательна).

16. Определения точек максимума, минимума и экстремума функции. Сформулировать необходимое условие экстремума. Критические точки.

Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Точка x₀ называется точкой минимума функции f, если для всех x из некоторой окрестности x₀ выполняется неравенство f(x) ≥ f(x₀.  Это наглядно показано на рисунке 1: 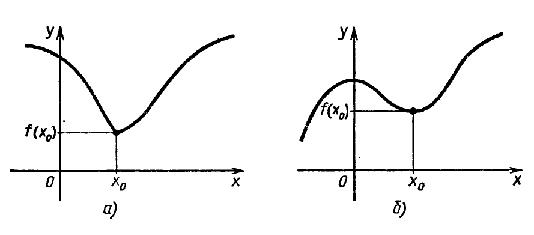   Определение. Точка x₀ называется точкой максимума функции f, если для всех x из некоторой окрестности x₀ выполняется неравенство f(x) ≤ f(x₀.  Это наглядно показано на рисунке 2: 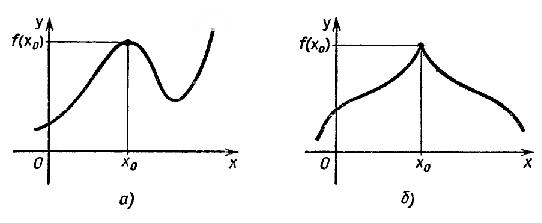   Критической точкой дифференцируемой функции  , где   — область в  , называется точка, в которой все её частные производные обращаются в нуль. Это условие эквивалентно обращению в нуль дифференциала функции в данной точке, а также равносильно горизонтальности касательной гиперплоскости к графику функции. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума функции.

(Необходимое условие экстремума) Если функция нескольких переменных u = f(x₁, x₂, … , x_n) имеет экстремум в некоторой точке, то в этой точке каждая ее частная производная равна нулю или не существует.