25. Метод интегрирования по частям

Метод интегрирования по частям

Это способ вычисления неопределенного интеграла, основанный на соотношении  (*) где u(x) и v(x) – непрерывно дифференцируемые функции, d(u(x)) и d(v(x)) – их дифференциалы. Для вычисления определенного интеграла справедлива аналогичная формула; разница, естественно, в том, что окончание вычисления здесь – применение формулы Ньютона-Лейбница, и выбор технической детали – пересчитывать ли пределы интегрирования при замене переменной или сначала вычислить неопределенный интеграл, а затем применить формулу Ньютона-Лейбница с пределами изменения исходной переменной. Приведём эту формулу:  .

26. Интегрирование дробно-рациональных функций. Интегрирование простых дробей

29. Задача о площади криволинейной трапеции

 Криволинейной трапецией называется фигура D с границей

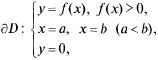
где функция (х) непрерывна (рис. 17.1).

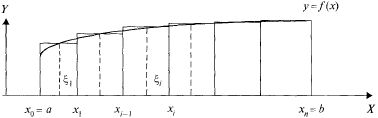
Найдем площадь криволинейной трапеции. Для этого разобьем отрезок [а, b] точками  на элементарных отрезков Обозначим   выберем произвольные точки и построим ступенчатую фигуру из прямоугольников с высотами  и основаниями Площадь ступенчатой фигуры и дает приближенное значение площади криволинейной трапеции. За точное значение площади естественно принять

29. Понятие определенного интеграла. Его свойства

Определенный интеграл — это аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых — интегрируемая функция или функционал, а вторая — область во множестве задания этой функции. Проще говоря, это интеграл, численно равный площади части графика функции в пределах от a до b, т. е. площади криволинейной трапеции.

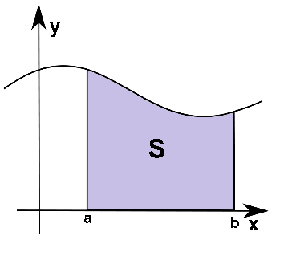
Определенный интеграл обозначается символом 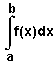 . Его можно найти по формуле Ньютона — Лейбниц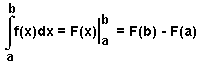а: св-ва

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.  , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

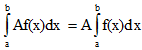
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
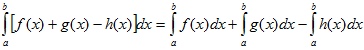
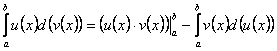