3. Теорема о дифференцировании суммы, произведении, частного (доказать для суммы).

Производная алгебраической суммы функций

выражается следующей теоремой.

Теорема 1. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

(u±v)' = u'±v'

Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

(u — v + w)' = u' — v' + w'

Производную произведения функций определяет

Теорема 2. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.

(uv)' = u'v + uv'

Следствие 1. Постоянный множитель можно выносить за знак производной (cv)' = cv' (с = const).

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные.

Например, (uvw)' = u'vw + uv'w + uvw'

Производная частного двух функций

выражается следующей теоремой.

Теорема 3. Производная частного двух дифференцируемых функций определяется формулой

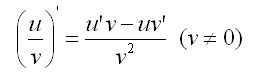
4. Сформулировать теорему о дифференцировании обратной функции

Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е

Доказательство 

Пусть   - дифференцируемая функция,  . Пусть   - приращение независимой переменной y и   - соответствующее приращение обратной функции  . Напишем тождество

Переходя в этом равенстве к пределу при  , которое влечет за собой стремление   к нулю ( ), получим:

, где   - производная обратной функции.

5. Сформулировать теорему о дифференцировании сложной функции.

Пусть функция z = f(x, y) дифференцируема в точке (x₀, y₀) и ее аргументы x = x(t) и y = y(t) дифференцируемы в точке t₀ , причем x(t₀) = x₀ , y(t₀) = y₀ .

Тогда сложная функция z = f(x(t), y(t)) переменной t дифференцируема в точке t₀ и ее производная вычисляется по формуле

6. Дифференцирование основных элементарных функций.

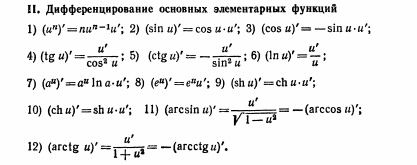
7. Логарифмическое дифференцирование

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.  Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:

Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.

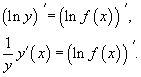
Отсюда видно, что искомая производная равна

8. Дифференцирование параметрически заданных функций.

Пусть функции x = (t) и y = ψ(t) определены на некотором отрезке [α, β]. Переменную t будем называть параметром.

Если x = (t) взаимно однозначна на отрезке [α, β], то она имеет обратную функцию t(x) =  ^{− 1} (x). Подставляя ее в равенство y = ψ(t), видим, что переменная y является сложной функцией переменной x:

 

y   =   ψ( − 1 (x) )   ≡   f(x) .

 

В этом случае говорят, что функция y = f(x) задана параметрически уравнениями

 

   x = (t) y = ψ(t)

(1)

 

где t  [α, β].