Билет №52 Экстремумы функций нескольких переменных

 

Рассмотрим функцию двух переменных (Пусть даны множества D Rⁿ и I R.

Определение. Если каждой точке множества D ставится в соответствие единственное число у из I, то говорят, что задана функция n переменных у=f(x₁, …, x_n). Множество D называется областью определения функции D(у)=D, множество I называется множеством значений функции I (у)= I.

Если зафиксировать любые n-1 переменные, то функция многих переменных превращается в функцию одной переменной. x₂=с₂, x₃=с₃, …, х_n=c_n; y=f(x₁, c₂, …, c_n) - функция одной переменной х₁.

)n=2, .

Определение 1. Точка (x₀, y₀)ÎR² называется точкой локального максимума (минимума) функции, если найдется некоторая окрестность данной точки (Определение 1. e-окрестностью точки х₀ÎR называется множество точек хÎR , удовлетворяющих условию

.

Определение 2. e-окрестностью точки х₀Î R² ( R³ ) называется множество точек плоскости (пространства), находящихся от точки х₀ на расстоянии, не превосходящем e.

), для всех точек которой выполняется условие ( ).

Определение 2. Точки локального максимума и минимума называются точками экстремума.

Теорема 1 (необходимое условие экстремума функции). Если точка (x₀, y₀) является точкой локального экстремума функции, то в этой точке частные производные(Рассмотрим функцию двух переменных n=2; z=f(x,y).

Определение. Частной производной функции z=f(x,y) в точке (x₀, y₀) D(у) по соответствующей переменной называется предел отношения частного приращения функции по этой переменной к приращению этой переменной, когда приращение переменной стремится к нулю (если этот предел существует и конечен).

,

) равны нулю или не существуют.

Доказательство. Пусть (x₀, y₀)Î R² - точка экстремума функции. Зафиксируем y₀ и рассмотрим функцию одной переменной.

.

Точка х₀ является точкой локального экстремума функции , следовательно, в этой точке производная или не существует, тогда частная производная равна нулю или не существует.

Аналогично доказывается, что или не существует.

Определение 3. Точки, в которых частные производные равны нулю или не существуют, называются стационарными точками функции многих переменных.

Необходимое условие экстремума не является достаточным, т. е. не каждая критическая точка является точкой экстремума. Например, функция имеет частные производные

, .

В точке (0,0) частные производные функции равны нулю, однако в этой точке у функции нет экстремума. Данная точка является седловой точкой графика.

 

Z

0 Y

X

 

Теорема 2 (достаточное условие экстремума функции). Пусть функция z=f(x,y) определена в некоторой окрестности критической точки (x₀, y₀), в которой частные производные равны нулю:

, ;

в этой точке функция имеет непрерывные частные производные второго порядка

, , .

Тогда если D=AC-B²>0, то в точке (x₀, y₀) функция имеет экстремум, причем если А<0 - максимум, если А>0 - минимум. В случае D=AC-B²<0 функция экстремума не имеет. Если D=AC-B =0 , то вопрос о наличии экстремума остается открытым.

Билет №53

Условные экстремумы

U=f(x1,x2,…,xn)

При ограничениях: - уравнения связи

Метод Лагранжа

L(x1,x2,…,xn: )= m – количество лямбд = количеству дополнительных условий = f(x1,x2,…,xn)+ -множитель Лагранжа

Задача об отыскании целевного экстремума и сводится к задаче об отыскании обычного экстремума функции L.

1) 2)

Условный экстремум функции 2-х переменных

U(x,y) при

L( )=f(x,y)+ (x,y)

(x0,y0)- точки возможного экстремума и 0

Если <0, тогда (x0,y0)- точка условного максимума

Если >0, тогда (x0,y0)- точка условного минимума

Если =0, тогда (x0,y0)- дополнительное исследование

Билет №54

Формула Тейлора для функции двух переменных

Теорема: Пусть U==f(M) M(x1,x2,…,xn) m+1 раз дифференцируема в некоторой окрестности т.М, тогда приращение этой функции в точке M и любой т.

из указанной окрестности можно записать в виде:

-формула Тейлора

Доказательство:

M(x1,x2,…,xi,…,xn); M1(x1,x2,…, ,…,xn)

df(M)= т.к. dx1=dx2=…=dxn=0, кроме dxi 0, dxi=

= =>

и т.д. по x1,x2,…,xn.

Билет №55

К омплексные числа. Действия над комплексными числами. Тригонометрическое и показательное представление комплексных чисел. y

мнимая еденица

Рассмотрим совокупность свободных векторов: M

ох – действительная ось

оy – мнимая ось i

( ) 0 1 x

x - Rez – действительная часть числа z

y – Imz – мнимая часть числа z

i=(0,1)=0+i1

Действия над комплексными числами

1. Сложение:

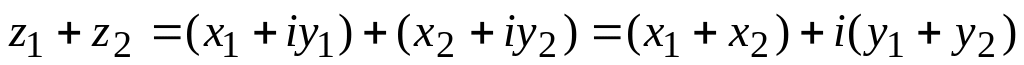
2. Вычитание:

3. Умножение:

4. Перемножение:

5. Частное:

6. Возведение в степень: ; ;

Тригонометрическая форма комплексного числа:

y p-модуль комплексного числа z

p=|z|

y p -аргумент комплексного числа z argz=

Argz= =arctg

0 x x

Если , то - главное значение аргумента

Обозначают Argz; Argz=argz+2 ; k – целое ;;; z= .