Плоскость наилучшей установки

Согласно формуле поперечной аберрации луча эта аберрация пропорциональна третей степени , поэтому ход лучей в ОС имеет следующий вид.

Огибающая семейства лучей образует поверхность каустики. Плоскость наилучшей установки (ПНУ) – называется плоскость экрана, установленная в наиболее узком месте каустики.

Продольная сферическая аберрация луча

Выше для представления сферической аберрации луча использовались отрезки в ПИ , которые называются поперечной аберрацией луча в меридиональной и сагиттальной плоскостях соответственно. Продольная аберрация это другой способ измерения сферической аберрции луча. Она связана с поперечной аберрацией.

Так как , если , то:

Графики сферической аберрации

Для наглядности отображения сферической аберрации ОС, используют следующие виды графиков, особенностью которых является то, что ось ординат ориентируют вдоль оптической оси системы, то есть она является горизонтальной линией.

Обычно представляют графики продольной и поперечной аберраций. Они представляют собой кубические (для поперечной) и квадратические (для продольной) параболы.

Ветви параболы направлены в положительную или отрицательную области соответственно знаку первой суммы Зейделя. Если сумма Зейделя положительная, то:

Сферическая аберрация одиночной линзы

Для исследования сферической аберрации линзы необходимо составить выражение для ее первой суммы Зейделя, выраженную через углы вспомогательных нулевых лучей.

Рассмотрим случай, когда , тогда в соответствии с условием нормировки

1,2 – главные плоскости поверхностей.

Если d=0 (линза тонкая), то:

Ищем выражение для Р₁:

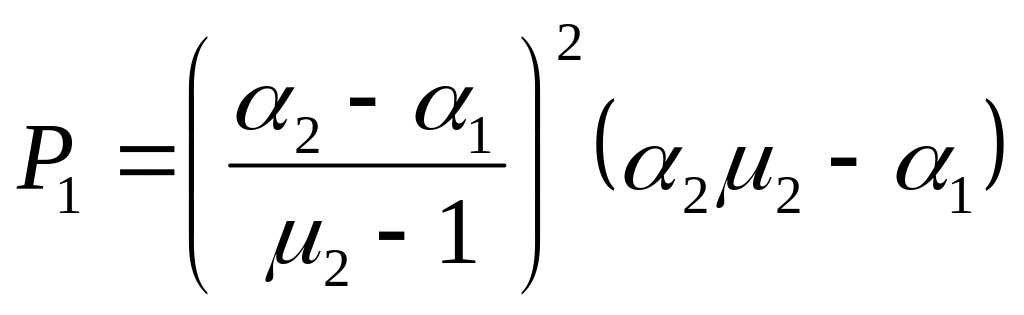
Так как согласно условиям нормировки - линейное увеличение в ПП (ПИ), то сферическая аберрация тонкой линзы в воздухе зависит от ₂, которая является свободным параметром.

Анализ полученного выражения показывает, что выражение в квадратных скобках ни при каких реальных значениях ₂ и (₁) не принимает нулевые значения. При изменениях ₂ во всем интервале (-;+) график функции Р=Р(₂) имеет вид.

Это означает то, что в тонкой линзе со сферическими поверхностями сферическая аберрация принципиально неустранима, однако видно, что при некотором значении ₂ параметр Р имеет минимальное значение, а следовательно и сферическая аберрация может иметь минимум. Для поиска указанного значения ₂, запишем:

Имея значения , а также можем рассчитать КП линзы, то есть ее радиусы и тем самым определить ее форму.

Для расчета радиусов используется формула, которая получается из формулы углов нулевого луча (

В частном случае, когда предмет находится на бесконечности

Так как оптическое стекло имеет показатель преломления n=1,5..2, то

Как видно из приведенных расчетов параметр ₂ определяет форму (прогиб) линзы.

Используя полученные результаты можно провести расчет ОС, состоящей из нескольких линз на минимум сферической аберрации. Исходными данными для расчета являются:

1.  - увеличение.

2. f^’ – фокусное расстояние ОС или ее оптическая сила Ф.

3. n – показатель преломления материала оптической детали (ОД).

4. m – количество линз в ОС.

1. Предполагается, что ОС тонкая, то есть толщины линз d=0. Так как количество линз m, то:

2. Предполагается, что работа линз в системе распределена равномерно. С учетом этого, а также того обстоятельства, что оптическая сила тонкой системы

3. Зная оптические силы каждой линзы можно рассчитать углы  между линзами, то есть все нечетные . Для этого воспользуемся формулой

Так как :

Для N=1: Для N=2:

Для N=3:

Значения нечетных углов  позволяют вычислить четные значения _2N, где N – номер линзы, по формуле, полученной выше.

Имея все углы 1ВНЛ (₁…_2m+1), а также, принимая условие , можно по формуле рассчитать все радиусы ОС.

Если предмет находится на бесконечности, то при m=2 ОС имеет обычно вид.