
- •Глава 4. Сложное движение.
- •§1. Сложное движение материальной точки.
- •1º. Постановка задачи о сложном движении точки.
- •2º. Связь между составляющими движениями в сложном движении материальной точки.
- •§2. Связь кинематических характеристик в сложном движении точки.
- •1º. Понятие кинематических характеристик составляющих движений
- •2º. Дифференцирование вектора, заданного в проекциях
- •3º. Теорема о сложении скоростей.
- •4º. Теорема о сложении ускорений в сложном движении материальной точки.
- •§3. Сложное движение твердого тела.
- •1º. Постановка задачи о сложном движении твердого тела.
- •2º. Скорости точек твердого тела в сложном движении.
- •2.1. Формула для скоростей точек твердого тела в сложном движении.
- •2.2. Теорема о сложении угловых скоростей.
- •§4. Кинематические уравнения Эйлера.
- •1º. Связь углов Эйлера и их производных.
- •2º. Общая схема построения кинематических уравнений Эйлера.
- •§5. Задача Дарбу. Кинематические уравнения Пуассона.
- •1º. Задача Дарбу.
- •2º. Кинематические уравнения Пуассона.
§3. Сложное движение твердого тела.
1º. Постановка задачи о сложном движении твердого тела.
Будем говорить, что тело совершает сложное движение, если оно движется в пространстве, которое, в свою очередь, движется, т.е. является подвижным пространством.
Определение 1.
Движение твердого тела относительно подвижного пространства и движение подвижного пространства относительно абсолютного называются составляющими сложного движения твердого тела.
Замечание 1.
Подвижное
пространство (в котором движется твердое
тело) может совершать движение в другом
подвижном пространстве, т.е. в пространстве,
движущемся в абсолютном. Тогда также
говорят, что это дополнительное подвижное
пространство является составляющим
движением сложного движения. Очевидно,
в общем случае можем говорить, что
твердое тело совершает сложное движение
с
![]() составляющими движениями.
составляющими движениями.
Основными задачами кинематики сложного движения является задача установления связи между абсолютным движением твердого тела и составляющими движениями, а также задача установления связи между кинематическими характеристиками составляющих движений и абсолютного движения твердого тела.
Будем
рассматривать решение указанных задач
в случае
![]() .
Результаты решения задач для
легко распространяются на случай
.
Результаты решения задач для
легко распространяются на случай
![]() .
.
Прежде чем приступить к решению поставленных задач, введем понятия мгновенной угловой скорости и мгновенного углового ускорения переносного и относительного движения твердого тела. Для этого сначала введем обозначения (см. рис.3):
— абсолютная система координат с полюсом в точке и базисом , , ;
— подвижная система координат с полюсом в точке и базисом , , ;
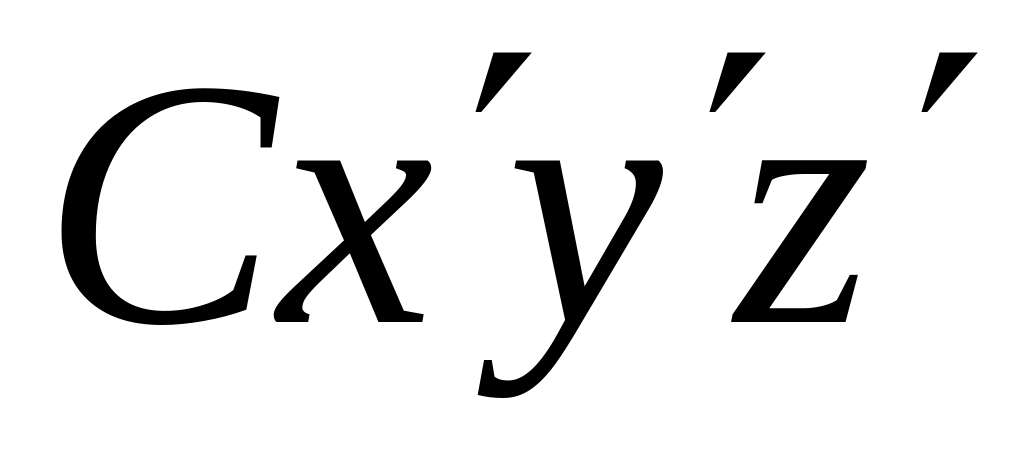 — связанная
с твердым телом система координат с
полюсом в точке
— связанная
с твердым телом система координат с
полюсом в точке
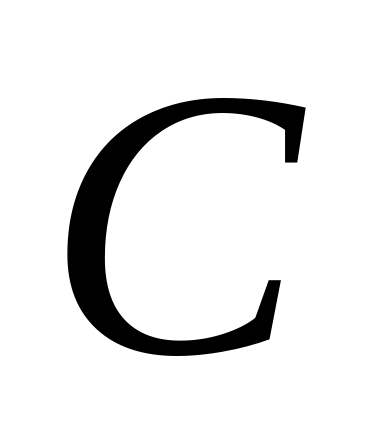 и базисом
и базисом
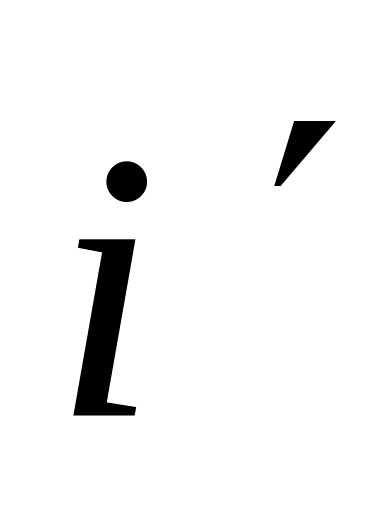 ,
,  ,
, 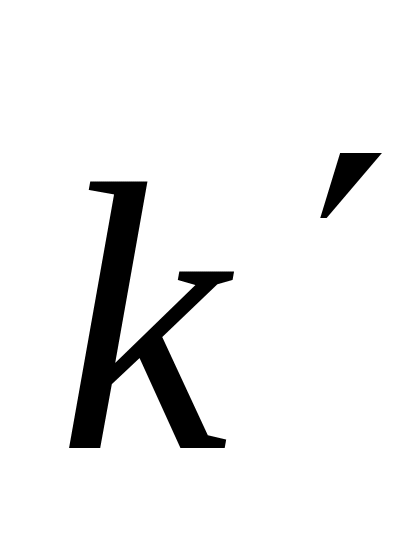 ;
;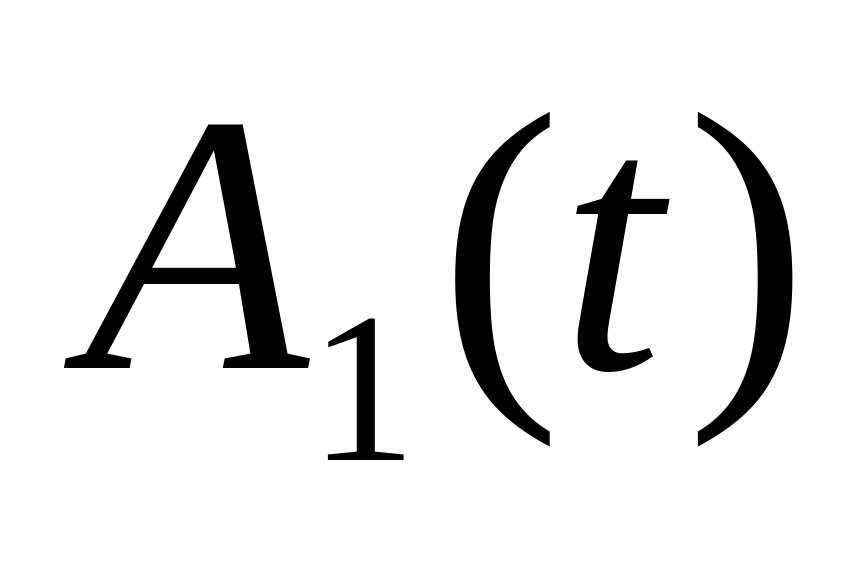 — матрица
ориентации подвижной системы
в абсолютном пространстве,
иначе, матрица
перехода от
к
;
— матрица
ориентации подвижной системы
в абсолютном пространстве,
иначе, матрица
перехода от
к
;
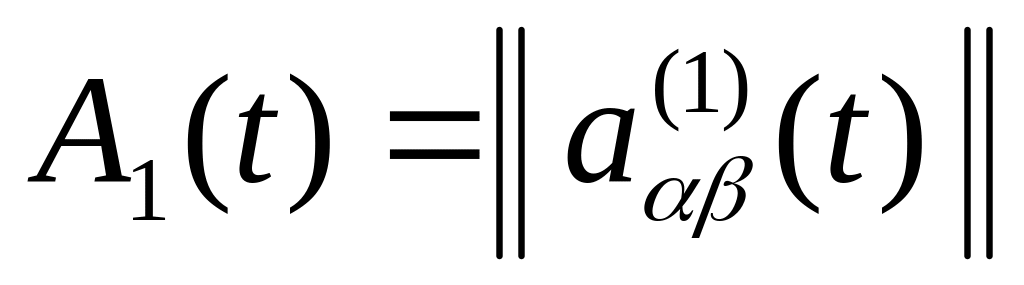 ,
,
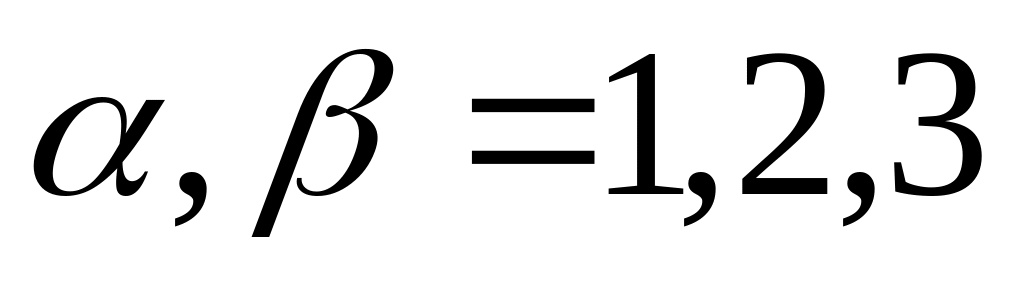 ;
;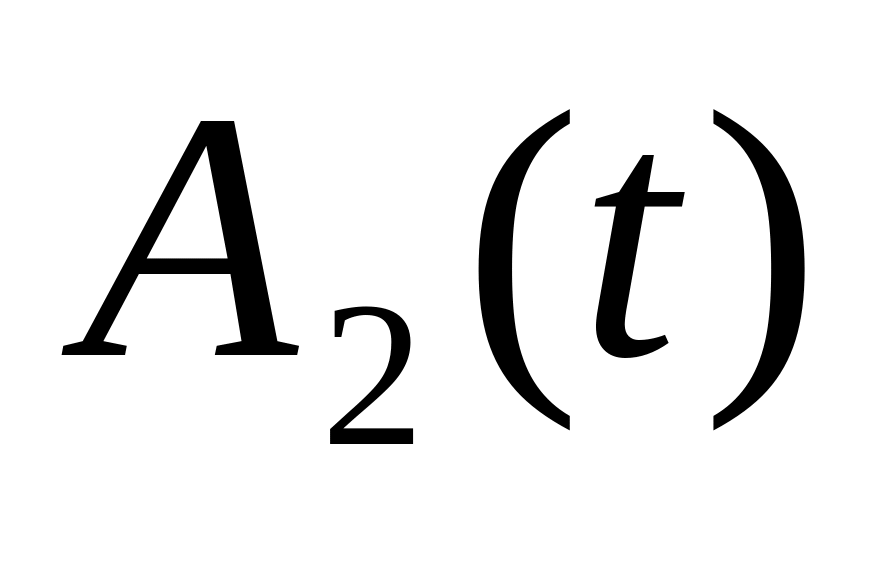 — матрица
ориентации твердого тела в подвижном
пространстве
,
иначе, матрица
перехода от
к
;
— матрица
ориентации твердого тела в подвижном
пространстве
,
иначе, матрица
перехода от
к
;
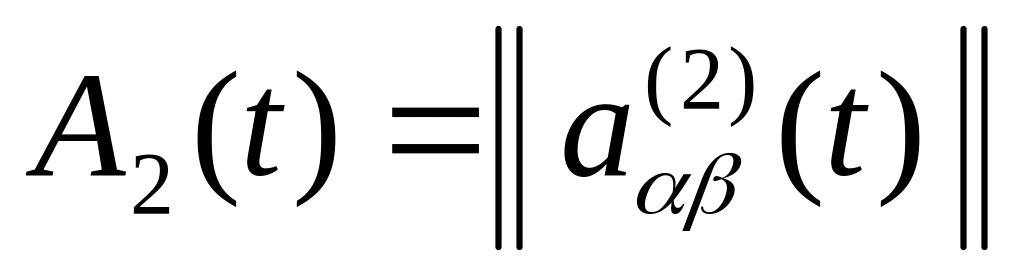 ,
.
,
.

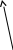
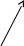
![]()
![]()
![]()
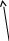


![]()



![]()
![]()


Рис.3.
Пусть — произвольно выбранная точка твердого тела. Введем обозначения для следующих векторов:
=![]() ,
,
![]() =
=![]() ,
=
,
=![]() ,
=
,
=![]() ,
,
![]() =
,
=
.
=
,
=
.
Здесь
— положение полюса подвижной системы относительно точки отсчета
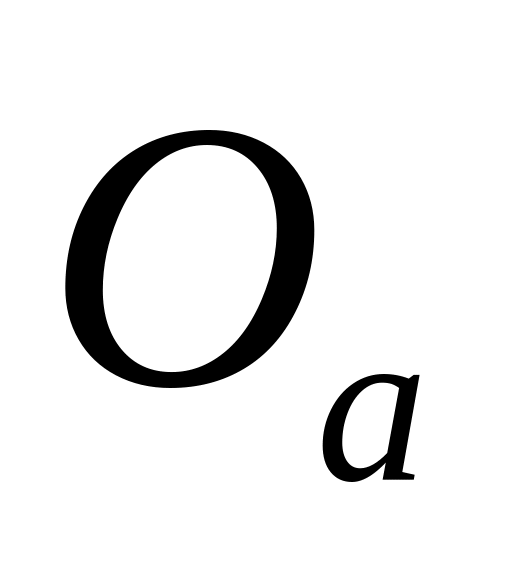 ,
выбранной в абсолютном пространстве;
оно задается абсолютными
координатами
,
выбранной в абсолютном пространстве;
оно задается абсолютными
координатами
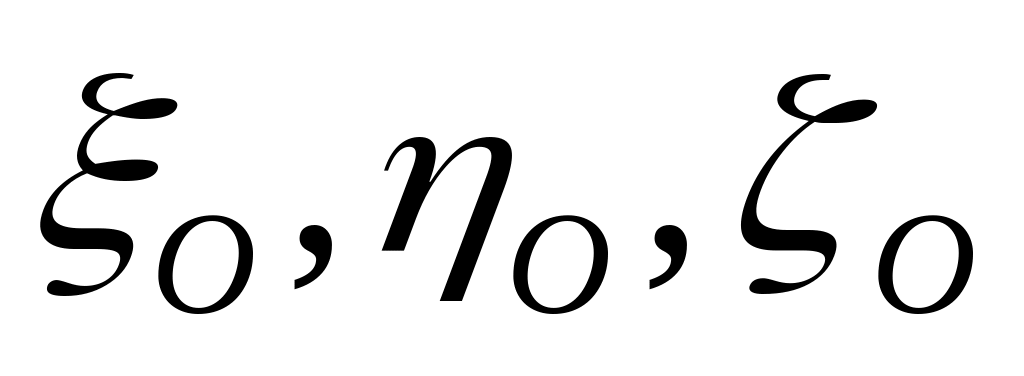 ;
;— положение полюса связанной с твердым телом системы координат относительно точки отсчета ; задается абсолютными координатами
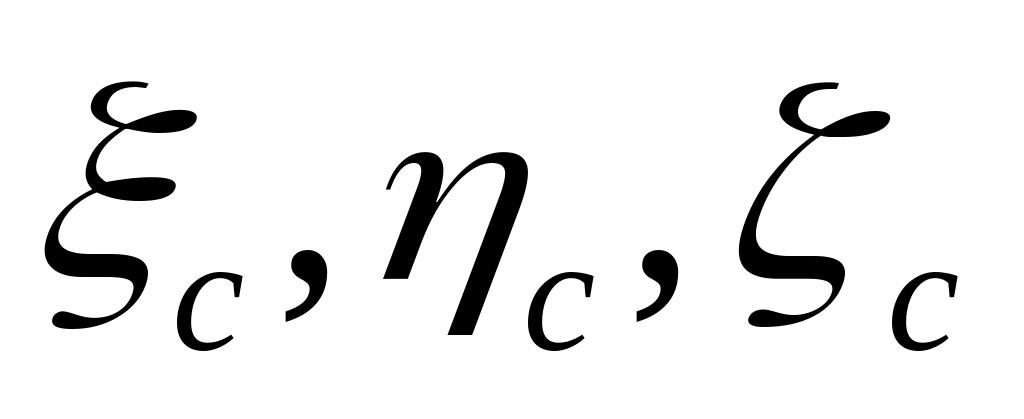 ;
;— положение полюса связанной системы относительно полюса подвижной системы ; задается координатами
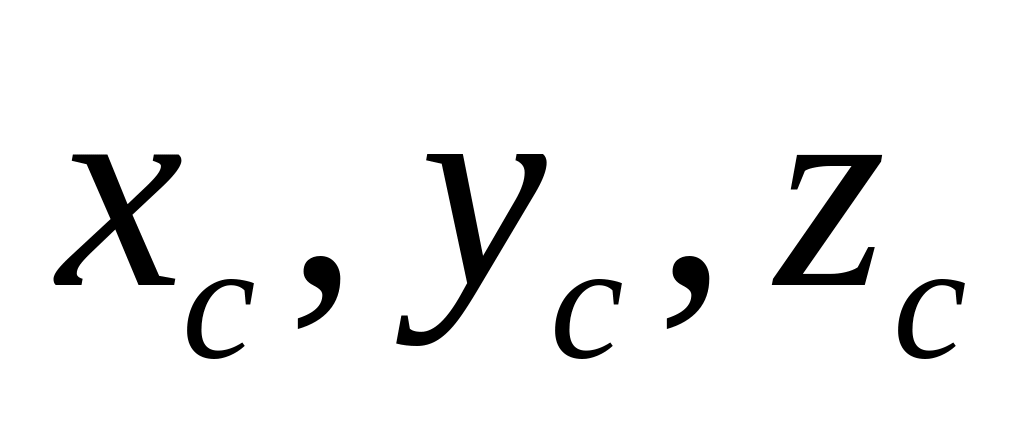 в подвижной системе
;
в подвижной системе
;— положение точки твердого тела в связанной системе ; задается координатами
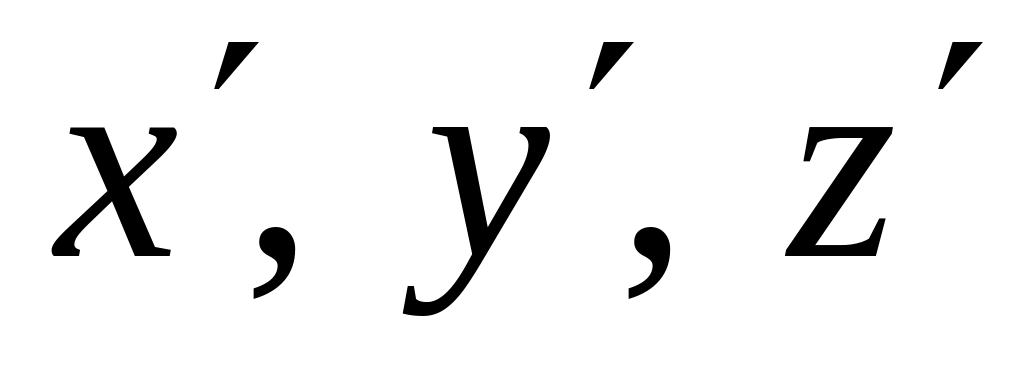 ;
;— положение точки твердого тела в подвижном пространстве ; задается координатами
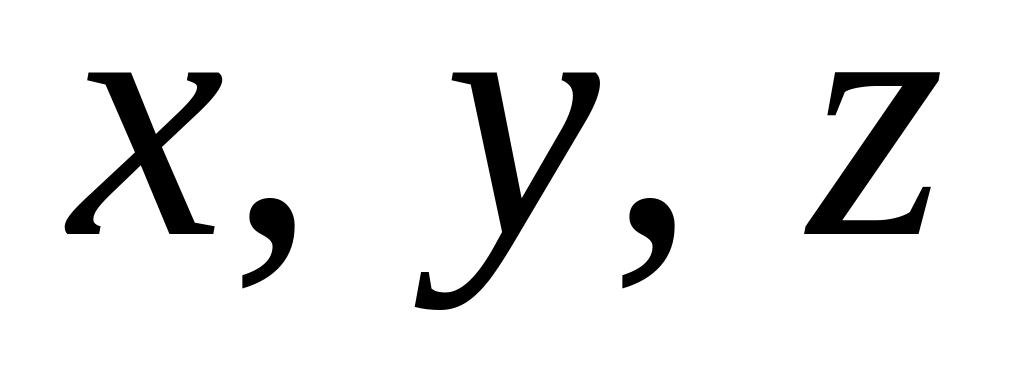 ;
;— положение точки твердого тела относительно точки отсчета в абсолютном пространстве; задается абсолютными координатами
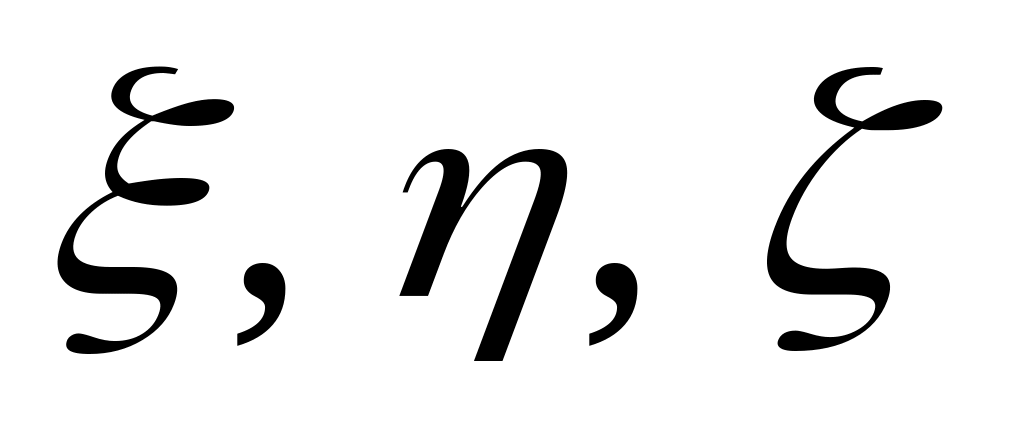 .
.
Теперь дадим понятия векторов мгновенной угловой скорости и мгновенного углового ускорения твердого тела в его переносном и относительном движениях.
Определение 2.
Переносной
мгновенной угловой скоростью ![]() и переносным мгновенным угловым
ускорением
и переносным мгновенным угловым
ускорением ![]() твердого
тела в его сложном движении называются
соответственно
вектор мгновенной угловой скорости и
вектор мгновенного углового ускорения
подвижной
системы
координат
относительно абсолютного пространства.
твердого
тела в его сложном движении называются
соответственно
вектор мгновенной угловой скорости и
вектор мгновенного углового ускорения
подвижной
системы
координат
относительно абсолютного пространства.
Сопоставляя данное определение 2 с определением 4 из §2 для векторов и , видим, что
= и = .
Как
и вектор
,
вектор
связан с движением базиса
![]() ,
,
![]() ,
,
![]() системы
в абсолютном пространстве в любой момент
времени
соотношением (5)
§2.
системы
в абсолютном пространстве в любой момент
времени
соотношением (5)
§2.
![]() . (1)
. (1)
В (1)
вектор-функции
,
,
задаются своими
проекциями на
оси абсолютной системы координат,
которые совпадают в каждый момент
с элементами матрицы ![]() соответственно: проекции вектор-функции
соответственно: проекции вектор-функции ![]() совпадают с элементами первого столбца,
совпадают с элементами первого столбца,
![]() — второго,
— третьего столбца. Поэтому можем
записать
— второго,
— третьего столбца. Поэтому можем
записать
![]() ,
,
![]() , (2)
, (2)
![]() .
.
Разложения
векторов
![]() ,
,
![]() ,
,
![]() по базису
,
,
получаются дифференцированием по
соотношений (2)
по базису
,
,
получаются дифференцированием по
соотношений (2)
![]() ,
,
![]() , (3)
, (3)
![]() .
.
Из
них следует, что координаты векторов
,
,
в абсолютной
системе в
момент времени
совпадают с
элементами соответствующих столбцов
матрицы ![]() :
координаты
— с первым
столбцом,
— со вторым,
— с третьим столбцом.
:
координаты
— с первым
столбцом,
— со вторым,
— с третьим столбцом.
Вектор
определяется либо дифференцированием
вектора
,
т.е.
=![]() ,
либо по формуле
,
либо по формуле
![]() . (4)
. (4)
В
ней разложение векторов
![]() ,
,
![]() ,
,
![]() по базису
,
,
в любой момент
времени
получается
дифференцированием по
соотношений (3).
Таким образом, будем иметь
по базису
,
,
в любой момент
времени
получается
дифференцированием по
соотношений (3).
Таким образом, будем иметь
![]() ,
,
![]() , (5)
, (5)
![]() .
.
Определение 3.
Вектором
мгновенной угловой скорости ![]() и вектором мгновенного углового ускорения
и вектором мгновенного углового ускорения
![]() относительного движения твердого тела
называются, соответственно, вектор
мгновенной угловой скорости и вектор
мгновенного углового ускорения твердого
тела при его движении относительно
подвижной системы координат
,
условно принимаемой неподвижной.
относительного движения твердого тела
называются, соответственно, вектор
мгновенной угловой скорости и вектор
мгновенного углового ускорения твердого
тела при его движении относительно
подвижной системы координат
,
условно принимаемой неподвижной.
Из данного определения следует, что
=![]() , (6)
, (6)
![]() . (7)
. (7)
Здесь
и
![]() означают условные
производные первого и второго порядка
от вектор-функций
означают условные
производные первого и второго порядка
от вектор-функций ![]() ,
заданных своими проекциями на оси
подвижной системы
через элементы матрицы
ориентации твердого тела в подвижном
пространстве. При таком дифференцировании
базис
,
,
системы
условно принимается неподвижным.
,
заданных своими проекциями на оси
подвижной системы
через элементы матрицы
ориентации твердого тела в подвижном
пространстве. При таком дифференцировании
базис
,
,
системы
условно принимается неподвижным.
Легко заметить, что выражения (6) и (7) для векторов и получаются из формул (1) и (4) путем замены в правых частях равенств (1) и (4):
подвижного базиса , , переносного движения на базис связанной системы координат ;
дифференцирования
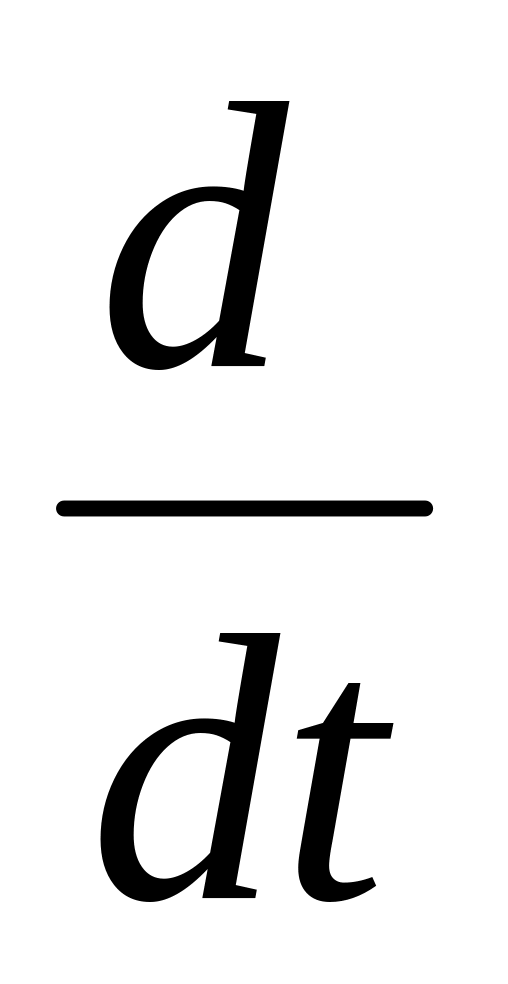 в абсолютной
системе на условное дифференцирование
.
в абсолютной
системе на условное дифференцирование
.
Поскольку векторы , , в проекциях на базис , , «условно неподвижной» системы координат в момент времени задаются элементами соответствующих столбцов матрицы перехода от связанной системы к системе , то можем записать
![]() ,
,
![]()
![]() , (8)
, (8)
![]()
![]() .
.
В (8) векторы , , , вообще говоря, зависят от . Однако в определении относительного движения твердого тела зависимость их от времени не учитывается. Движение твердого тела по отношению к системе отсчета является его движением в пространстве , условно принятом за абсолютное пространство.
Тем самым относительное движение тела определяется относительным движением полюса его связанной системы и движением базиса этой системы относительно базиса , , , условно принятого неподвижным.
Разложения
векторов
![]() ,
,
![]() ,
,
![]() по базису
,
,
получаются дифференцированием по
соотношений (8),
причем дифференцируются только
направляющие косинусы
по базису
,
,
получаются дифференцированием по
соотношений (8),
причем дифференцируются только
направляющие косинусы
![]() ,
,
а базис
,
,
не дифференцируется:
,
,
а базис
,
,
не дифференцируется:
![]() ,
,
![]() , (9)
, (9)
![]() .
.
Аналогичным дифференцированием соотношений (9) строятся разложения векторов
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
Очевидно, для векторов и в любой момент времени справедливы формулы Эйлера-Пуассона
![]() =
,
=
,
=
.
(10)
=
,
=
,
=
.
(10)
= , = , = . (11)
Соотношения (10) следуют из определения вектора мгновенной угловой скорости подвижной системы координат относительно абсолютного пространства (см. определение 4 в §2).
Формулы (11) вытекают из определения относительной производной от векторов , , , заданных своими проекциями на оси подвижной системы , и из определения 3 вектора мгновенной угловой скорости относительно системы (условно принятой неподвижной).
Примечание.
В дальнейшем слово «мгновенный» в названии векторов , , , будем опускать, если это не вызовет недоразумений.
Приступим теперь к решению первой задачи кинематики сложного движения твердого тела — установим связь между его абсолютным движением и составляющими движениями.
Очевидно, из правила сложения векторов имеем (см. рис.3)
=
+![]() +
.
+
.
Подставляя принятые обозначения, получаем
=
+![]() +
.
(12)
+
.
(12)
Учитывая,
что вектор
имеет координаты
![]() ,
, ![]() ,
, ![]() в системе
,
можем записать
в системе
,
можем записать
= + + .
Вектор задается координатами , , в связанной системе
=![]() ,
,
, , — постоянные величины для каждой точки твердого тела.
Если представить правую часть равенства (12) в проекциях на абсолютные оси, то в векторно-матричной форме равенство (12) примет вид:
=
+
![]() +
+![]() .
(13)
.
(13)
Здесь
под вектором
![]() понимается вектор
,
имеющий координаты
в подвижной системе, вычисляемые по
формуле
понимается вектор
,
имеющий координаты
в подвижной системе, вычисляемые по
формуле
![]() .
.
Под
вектором
+
понимается вектор
![]() .
Он имеет координаты
в абсолютной системе
,
которые вычисляются по формуле
.
Он имеет координаты
в абсолютной системе
,
которые вычисляются по формуле
![]() +
+
![]() .
.
Соотношение (13) задает связь абсолютного движения любой точки твердого тела, имеющей координаты , , в связанной системе , с составляющими движениями, задаваемыми вектор-функцией и матрицей ориентации (это первое составляющее движение), вектор-функцией и матрицей ориентации твердого тела в подвижном пространстве (это второе составляющее движение).
Таким образом, формула (13) дает решение первой задачи кинематики сложного движения твердого тела.
Замечание 2.
Соотношение (13) может быть получено непосредственно из теоремы связи абсолютного движения и составляющих движений материальной точки, доказанной в §1, п.2º. Действительно, каждая точка твердого тела совершает сложное движение. В соответствии с указанной теоремой ее абсолютное движение связано с переносным и относительным по формуле (18) из §1, п.2º.
В задаче о сложном движении твердого тела переносное движение точки определяется функцией
![]() =
+
=
+
![]() .
.
Здесь = – положение точки в подвижном пространстве , которое при построении функции условно считается постоянным. Относительное движение точки описывается функцией
=![]() =
+
,
=
+
,
определяемой
из формулы задания движения твердого
тела в подвижной системе координат
.
В ней
=
– положение точки
в связанной системе ![]() .
Оно является неизменным в этой системе.
.
Оно является неизменным в этой системе.
Суперпозиция функций и = , задающих переносное и относительное движения точки , с одной стороны, приводит к соотношению (13). С другой стороны, согласно указанной теореме, она определяет связь абсолютного движения и составляющих движений точки .
Поскольку полученное соотношение (13) справедливо для любой точки твердого тела, то этим установлена связь абсолютного и составляющих движений твердого тела.
