
- •5. Модель Буллена:
- •11.Действие силы тяжести и центробежной силы на точечную массу на пов. Земли:
- •13. Значения гравитационного и полярного сжатия:
- •15.Понятие геоида:
- •17. Редукция Фая и Буге, аномалии Фая и Буге:
- •2 0. Три основных прилива, положение их фронтов.
- •21. Прямые и обратные задачи гравиметрии. Поле точечной массы шара:
- •27. Шкала инверсий магнитного поля Земли за последние 4,5 млн. Лет:
- •29. Элементы земного матнетизма. Опр. Пол. Векторов t, z, h, j, d.
- •36. Магнитное поле верт. Тонкого пласта:
- •37. Магнитное поле верт. Толстого пласта:
- •42. Определение залегания нижних кромок по формуле Булиной.
- •44. Акустическое давление и кол. Скорость плоской волны. Акустический импеданс:
- •46. Лучи и годографы отраженной волны. Вывод уравнения:
- •51. Акустическое давление и колебательная скорость сферической волны:
- •52. Отражение звука от границы вода-дно, написать общ. Ур-ние. Формула Релея, ее анализ для коэффициента отражения от мягкого и скального грунта:
- •53. Геометрическая сейсмика. Лучи и годографы рефрагиро-ванной волны:
- •55. Статистический анализ годографов:
44. Акустическое давление и кол. Скорость плоской волны. Акустический импеданс:
Введение
понятия звукового потенциала U
позволяет определить ряд важных
параметров плоской волны. Потенциал U
в безграничной среде определяется
выражением:
![]() Производная потенциала U
по времени, умноженная на плотность
среды ,
характеризует акустическое давление
P
плоской волны:
Производная потенциала U
по времени, умноженная на плотность
среды ,
характеризует акустическое давление
P
плоской волны:
![]() Амплитуда акустического давления Pm
равна:
Амплитуда акустического давления Pm
равна:
![]() Производная потенциала U
по направлению x
определяет колебательную скорость
плоской волны:
Производная потенциала U
по направлению x
определяет колебательную скорость
плоской волны:
![]() Амплитуда колебательной скорости Vm
равна:
Амплитуда колебательной скорости Vm
равна:
![]() Величина
Величина
![]() называется
волновым числом, показывающим, сколько
длин волн
укладывается на расстоянии x
=
2,
т.е.
называется
волновым числом, показывающим, сколько
длин волн
укладывается на расстоянии x
=
2,
т.е.
![]() Сравнивая выражения и, видим, что под
знаком синуса стоит одно и то же выражение
Сравнивая выражения и, видим, что под
знаком синуса стоит одно и то же выражение
![]() .
Это значит, что в плоской волне акустическое
давление P
и колебательная скорость V
распространяются синфазно. Взяв отношение
.
Это значит, что в плоской волне акустическое
давление P
и колебательная скорость V
распространяются синфазно. Взяв отношение
![]() ,
получим:
,
получим:
![]() ;
таким образом,
;
таким образом,
![]() Полученное выражение называется
акустическим сопротивлением (импедансом)
среды.
Полученное выражение называется
акустическим сопротивлением (импедансом)
среды.
45.
Скорость продольных и поперечных волн.
Отношение Cp/Cs.
через
модуль Юнга и модуль сдвига можно
определить скорость распространения
упругих волн – объемных, называемых
продольными волнами ср
– и сдвиговых волн, называемых поперечными
волнами – сs:
(м/с);
(м/с), где
– плотность среды. Существует весьма
важное соотношение скорости продольных
волн к скорости поперечных – ср/сs,
которое является, по существу, функцией
коэффициента Пуассона:
![]() Для осадочных пород, вследствие низкого
сопротивления сдвигу рыхлых отложений,
величина ср/сs
может достигать больших значений:
ср/сs
= 1,4
14 и более. Для кристаллических магматических
и метаморфических пород это соотношение
лежит в более узких пределах:
ср/сs
=
1,7
1,9. Из приведенного видно, что скорость
упругих волн в породах зависит главным
образом от их плотности и практически
не зависит от частоты колебаний. Последняя
оказывает сильное влияние на поглощение
волн.
Для осадочных пород, вследствие низкого
сопротивления сдвигу рыхлых отложений,
величина ср/сs
может достигать больших значений:
ср/сs
= 1,4
14 и более. Для кристаллических магматических
и метаморфических пород это соотношение
лежит в более узких пределах:
ср/сs
=
1,7
1,9. Из приведенного видно, что скорость
упругих волн в породах зависит главным
образом от их плотности и практически
не зависит от частоты колебаний. Последняя
оказывает сильное влияние на поглощение
волн.
46. Лучи и годографы отраженной волны. Вывод уравнения:
Пусть скорость звука увеличивается с глубиной по линейному закону:
![]() где
c0
– некоторое постоянное значение скорости
звука, измеренное в приповерхностном
слое осадков на глубине h0;
c1
– на глубине h1.
Тогда отношение
где
c0
– некоторое постоянное значение скорости
звука, измеренное в приповерхностном
слое осадков на глубине h0;
c1
– на глубине h1.
Тогда отношение
![]() определять величину вертикального
градиента скорости звука в воде. С учетом
величина
a
в выражении будет равна
определять величину вертикального
градиента скорости звука в воде. С учетом
величина
a
в выражении будет равна
![]() Если разбить градиентный слой на
бесконечное множество тонких слоев, то
на границе каждого из них падающий луч
испытывает преломление согласно
известному закону:
Если разбить градиентный слой на
бесконечное множество тонких слоев, то
на границе каждого из них падающий луч
испытывает преломление согласно
известному закону:
![]() Время пробега вдоль луча OMX0
определится из выражения
Время пробега вдоль луча OMX0
определится из выражения
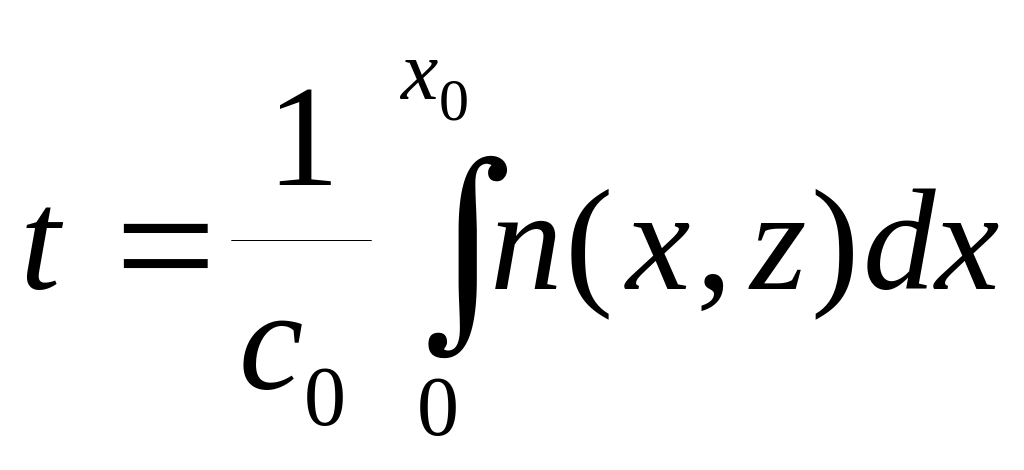
![]()
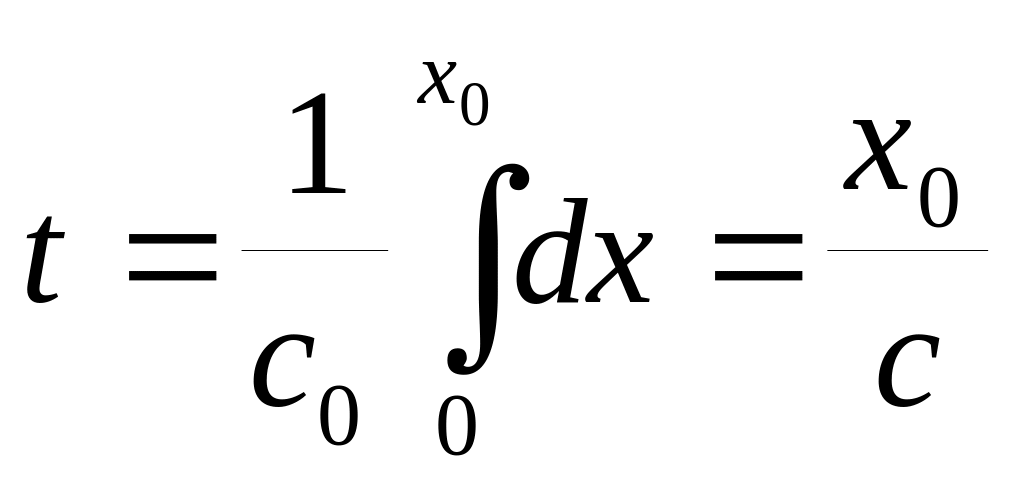
![]() Это и есть уравнение годографа отраженной
от поверхности слоя волны. Годограф
представляет собой гиперболу, минимум
которой совпадает с началом координат
(x
=
0). Таким образом, годограф характеризует
зависимость времени прихода отраженной
(в данном случае) волны от расстояния.
Используя полученное значение c0,
по формулам (IX.11) нетрудно определить
глубину H
до слоя. Годограф отраженной волны
обладает следующими свойствами. 1. Каждый
из лучей выходит из начала координат,
симметричен относительно вертикальной
прямой, что проходит через его вершину.
2. Годографы из любого пункта взрыва,
отходящие в противоположные стороны,
симметричны относительно прямой,
проходящей через пункт взрыва вертикально.
Если эти признаки не соблюдаются, то
среда вертикально неоднородна.
Это и есть уравнение годографа отраженной
от поверхности слоя волны. Годограф
представляет собой гиперболу, минимум
которой совпадает с началом координат
(x
=
0). Таким образом, годограф характеризует
зависимость времени прихода отраженной
(в данном случае) волны от расстояния.
Используя полученное значение c0,
по формулам (IX.11) нетрудно определить
глубину H
до слоя. Годограф отраженной волны
обладает следующими свойствами. 1. Каждый
из лучей выходит из начала координат,
симметричен относительно вертикальной
прямой, что проходит через его вершину.
2. Годографы из любого пункта взрыва,
отходящие в противоположные стороны,
симметричны относительно прямой,
проходящей через пункт взрыва вертикально.
Если эти признаки не соблюдаются, то
среда вертикально неоднородна.
47.
Лучи и годографы преломленной волны.
Вывод уравнения: В
случае мягкого грунта (R1
=
0,1-0,3) и безградиентного слоя воды возможно
образование преломленной и рефрагированной
волн (рис. 64). Тогда согласно закону
преломления, и в предельном случае
заворота луча, когда
![]() ,
имеем
,
имеем
![]() Выражение
Выражение
![]() называется кажущейся скоростью и
характеризует скорость распространения
фронта волны вдоль поверхности дна.
Следовательно,
называется кажущейся скоростью и
характеризует скорость распространения
фронта волны вдоль поверхности дна.
Следовательно,
![]() ,
,![]() т.е.
кажущаяся скорость в точке выхода луча
на поверхность дна должна быть равна
скорости в вершине заворота (рефракции)
луча под дном моря. Как было показано
выше, условием образования головной
преломленной волны является равенство:
т.е.
кажущаяся скорость в точке выхода луча
на поверхность дна должна быть равна
скорости в вершине заворота (рефракции)
луча под дном моря. Как было показано
выше, условием образования головной
преломленной волны является равенство:![]() ;
для границы вода-дно и, соответственно,
для границ в консолидированной коре:
;
для границы вода-дно и, соответственно,
для границ в консолидированной коре:
![]()
![]() и есть уравнение годографа преломленной
на первой границе вода-дно волны.
и есть уравнение годографа преломленной
на первой границе вода-дно волны.
48.
Уравнение зависимости гл. проникновения
рефр. волны от длинны годографа.
![]() Это и есть уравнение годографа
рефрагированной волны для линейного
закона изменения скорости. Лучи и
годографы показаны на. При других законах
изменения скорости с глубиной годограф
будет иметь иной вид. Каждую точку
годографа рефрагированной волны можно
рассматривать как точку вступления
фиктивной головной волны. Поэтому О.К.
Кондратьев предложил рассчитывать
глубину проникновения луча по формуле:
Это и есть уравнение годографа
рефрагированной волны для линейного
закона изменения скорости. Лучи и
годографы показаны на. При других законах
изменения скорости с глубиной годограф
будет иметь иной вид. Каждую точку
годографа рефрагированной волны можно
рассматривать как точку вступления
фиктивной головной волны. Поэтому О.К.
Кондратьев предложил рассчитывать
глубину проникновения луча по формуле:
![]()
49.
Трансформация в верхнее полупространство:
При
геофизических, гравимагнитных
исследованиях, например в океане,
измерительный комплекс аппаратуры
помещается либо на корабле, либо в
приповерхностном слое воды.
Аномалиеобразующие тела залегают в
толще земной коры на различных уровнях
подо дном океана. Поэтому все измерения,
производимые фактически с поверхности
воды, как бы удалены от объектов в верхнее
полупространство на расстояние, равное
глубине океана в точке наблюдения.
Расчет поля в верхнее полупространство
можно производить с помощью интеграла
Пуассона:
![]() В основе пересчета потенциальных полей
в нижнее полупространство лежит следующее
свойство потенциальных функций: значение
функции в центре окружности (плоская
задача) равно ее среднему значению по
окружности (рис. 55). Используя это
свойство, наблюденное значение функции
g(x)
или T
в произвольной точке (0, 0) профиля можно
рассматривать как значение в центре
круга. На этом основании для вычисления
значений g
и T
в точке (0, -h)
нижнего полупространства можно положить
значение функции в центре приблизительно
равным среднему арифметическому в
четырех равноотстоящих на окружности
точках с радиусом h,
т.е.
В основе пересчета потенциальных полей
в нижнее полупространство лежит следующее
свойство потенциальных функций: значение
функции в центре окружности (плоская
задача) равно ее среднему значению по
окружности (рис. 55). Используя это
свойство, наблюденное значение функции
g(x)
или T
в произвольной точке (0, 0) профиля можно
рассматривать как значение в центре
круга. На этом основании для вычисления
значений g
и T
в точке (0, -h)
нижнего полупространства можно положить
значение функции в центре приблизительно
равным среднему арифметическому в
четырех равноотстоящих на окружности
точках с радиусом h,
т.е.
![]() Следует отметить, что при пересчете в
нижнее полупространство сильно возрастают
влияния ошибок измерений.
Следует отметить, что при пересчете в
нижнее полупространство сильно возрастают
влияния ошибок измерений.
50.
Вывод волнового уравнения: Нужно
найти уравнение возникающих гармонических
колебаний частиц в горной породе. ma=F,
где а
– ускорение, m
– масса
частицы,
![]() Величина U
= x
характеризует смещение частиц от некоего
положения равновесия. Обозначим массу
частицы как произведение объема V
на плотность :
m = V·
= xyz·.
Величина U
= x
характеризует смещение частиц от некоего
положения равновесия. Обозначим массу
частицы как произведение объема V
на плотность :
m = V·
= xyz·.
![]() Если силы действуют вдоль одной оси x,
то сумма всех сил F
будет равна сумме напряжений x,
действующих на соответствующую площадь
(объем) S:
Если силы действуют вдоль одной оси x,
то сумма всех сил F
будет равна сумме напряжений x,
действующих на соответствующую площадь
(объем) S:
![]() где
S
=
xyz.
где
S
=
xyz.

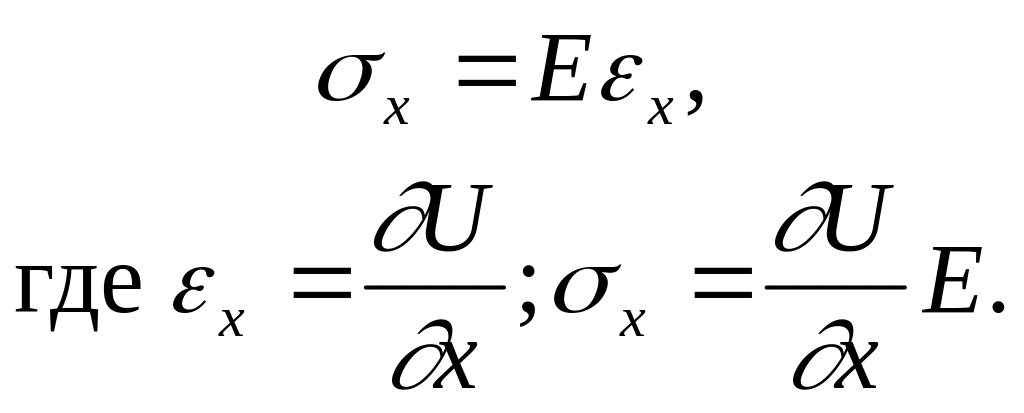 В итоге получаем волновое уравнение
вида:
В итоге получаем волновое уравнение
вида:
![]() Здесь коэффициент
Здесь коэффициент
![]() есть не что иное, как квадрат скорости
распространения продольной волны в
породе сp:
есть не что иное, как квадрат скорости
распространения продольной волны в
породе сp:
![]() Это и есть уравнение распространения
упругих гармонических колебаний части
среды вдоль координаты x,
фронт которых имеет вид плоскости.
Отсюда название – уравнение плоских
волн.
Это и есть уравнение распространения
упругих гармонических колебаний части
среды вдоль координаты x,
фронт которых имеет вид плоскости.
Отсюда название – уравнение плоских
волн.
