5 Описание перемещений и деформаций объектов план раздела
Перенос, масштабирование и поворот двумерной точки.
Однородные координаты.
Матричное представление трехмерных преобразований.
Геометрическая интерпретация компонент матриц поворота.
Матрицы обратных преобразований.
Композиция нескольких преобразований.
Проблема коммутативности перемножения матриц преобразований.
ПРИМЕР: отображение прямоугольника в другую систему координат.
Перенос, масштабирование и поворот двумерной точки Обычный линейный перенос…
Можно все это описать обычными уравнениями. Но матричная запись оказывается удобнее.
Масштабирование координат
Это преобразование, при котором новое значение координаты получается умножением старого на число, называемое коэффициентом масштабирования. Так можно преобразовывать, например, каждую координату по отдельности.
А можно и обе сразу.
В этом случае матричная запись оказывается опять удобнее. Матрица S, называемая матрицей масштабирования, имеет вид:
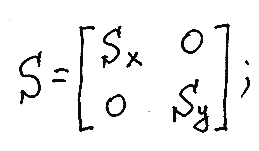
Новые значения координат точки Р вычисляются с ее помощью так:
,
что кратко записывается через равенство:
Интересный частный случай.
Нередко приходится находить положение точки, симметричное заданному относительно некоторой координатной оси. В этом случае значение координаты меняет свой знак на обратный. По сути эта операция означает масштабирование требуемой координаты с коэффициентом масштабирования -1 и описывается так
Но эта же операция имеет и другую трактовку: смена направления координатной оси на противоположное. Матрица масштабирования та же, но ориентация системы координат с правой меняется на левую или наоборот.
Поворот (вокруг начала координат)
Из курса аналитической геометрии на плоскости известны формулы, описывающие такое преобразование.
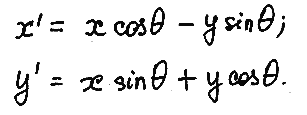
На основании этой системы уравнений легко формируется матрица R, называемая матрицей поворота:
Новоые координаты точки вычисляются так:
Что кратко записывается уравнением:
Неоднородность описаний
Обобщая вышесказанное, нетрудно заметить, что три базовых трансформации (перемещение, поворот и масштабирование) описываются РАЗНЫМИ матричными действиями. Масштабирование и поворот сводятся к умножению:
Перемещение сводится к матричному сложению. Это плохо, потому что затрудняет описание сложных преобразований, состоящих из цепочки действий.
Как перемещение описать умножением?
Проблема состоит в поиске такого математического описания перемещения, которое сводилось бы к умножению матриц, что сделает набор действий однородным. Как мы увидим, это возможно.
Исходные уравнения для перемещения имеют вид:
Добавим в правые части уравнений по дополнительному нулевому слагаемому (что не нарушит равенства) и придадим уравнениям следующий вид:
Что в матричной форме легко записывается так:
Если добавить еще третье матричное тождество
То в итоге система уравнений для вычисления координат точки после перемещения приобретает вид:
Входящая в правую часть матрица 3х3 называется матрицей перемещения:
С ее помощью перемещение описывается через умножение матриц. Цель достигнута.
Однородные координаты
Предыдущий вопрос породил новую проблему. Вместо описания точки как пары координат на плоскости
Используется описание через координату х и у и в матрицу-строку точки вводится еще единица:
Такое видоизмененное представление точки на плоскости принято называть ОДНОРОДНЫМИ координатами. Впервые их ввел E.A.Maxwell (Camdridge, 1946 г.)
Теперь с их помощью все операции математически описываются однородно – через умножение матриц.
МАТРИЧНОЕ ОПИСАНИЕ НЕСКОЛЬКИХ ТРАНСФОРМАЦИЙ
Рассмотрим, как записываются матрицы сложных преобразований, но состоящих из цепочки однотипных пребразований.
Несколько перемещений
Векторная схема нескольких (здесь двух) перемещений выглядит так:
Промежуточная точка Р1 из исходной Р0 получается так:
Конечная точка Р2 из точки Р1 получается аналогично.
Итоговая матрица двойого перемещения имеет приводимый ниже вид. Легко видеть, что он полностью согласуется с векторным описанием двойного перемещения.
Несколько масштабирований
Предположим, сначала выполняется масштабирование с матрицей Sx1, а затем, от его результирующего положения, второе – с матрицей Sx2:
Составляющие трансформации описываются классическими уравнениями:
Сводя эти уравнения в одно, получаем:
Откуда можно выделить матрицу результирующего масштабирования.
Несколько поворотов
Как и в предыдущем случае, рассмотрим два последовательных поворота:
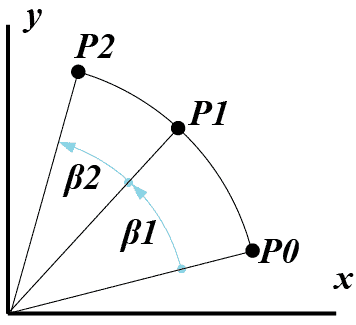
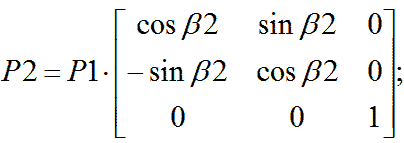
Матрица результирующего поворота имеет вид:
И вообще, несколько однотипных преобразований на плоскости:
Здесь приведены обобщающие формулы матриц, описывающих результирующие матрицы для любого числа составляющих однотипных преобразований.
МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ТРЕХМЕРНЫХ ПРЕОБРАЗОВАНИЙ
Исходные соображения
Трехмерная точка в однородных координатах
P = [ x y z 1 ].
Система координат – ПРАВАЯ.
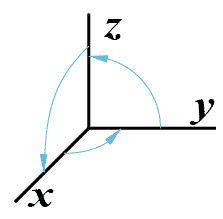
Поворотов теперь три – вокруг каждой оси.
(показаны положительные направления)
ЛИНЕЙНОЕ ПЕРЕМЕЩЕНИЕ в 3Д
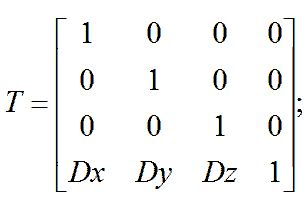
МАСШТАБИРОВАНИЕ в 3Д
ПОВОРОТЫ в 3Д
Поворот погруг оси Z:
Поворот вокруг оси Х:
Поворот вокруг оси Y:
ГЕОМЕТРИЧЕСКАЯ ТРАКТОВКА КОМПОНЕНТОВ МАТРИЦЫ ПОВОРОТА
Матрица, описывающая поворот точки на плоскости вокруг начала координат
может иметь трактовку, облегчающую восстановление матрицы при известных начальном и конечном положениях точки, но неизвестной матрицеповорота.
ВАРИАНТ 1
Столбцы матрицы поворота можно рассматривать как проекции двух ортогональных единичных векторов, которые ПОСЛЕ поворота на заданный угол СОВМЕЩАЮТСЯ с координатными осями.
ВАРИАНТ 2
Строки матрицы поворота можно рассматривать как проекции двух ортогональных единичных векторов, которые ДО поворота СОВПАДАЛИ с координатными осями, а потом были повернуты на заданный угол.
МАТРИЦЫ ОБРАТНЫХ ПРЕОБРАЗОВАНИЙ
ПОСТАНОВКА ПРОБЛЕМЫ
Предположим, мы знаем результат (Р1) некоторого преобразования, тип которого нам известен. Известна и сама матрица. Надо восстановить исходное положение точки.
Итак, что дано: а) Результат преобразования – Р1.
б) Вид преобразования (вид матрицы МП – то ли это
Т, то ли S, то ли R);
в) матрица преобразования М ( М Î { T, S, R} ).
Найти: исходную точку Р0.