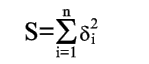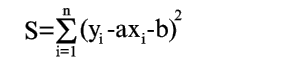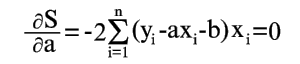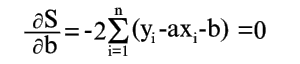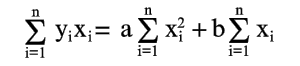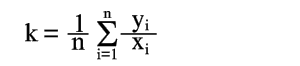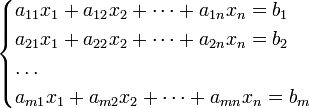- •Классификация методов решения слау
- •[Править]Прямые методы
- •[Править]Итерационные методы
- •Погрешность численного дифференцирования
- •Итерационные методы решения слау Итерационные методы решения линейных алгебраических систем Метод простой итерации или метод Якоби
- •Метод Гаусса – Зейделя
- •Метод Гаусса решения слау
- •[Править]Условие совместности
- •Метод Эйлера
- •[Править]Оценка погрешности
- •[Править]Значение метода Эйлера
- •Метод прогонки решения слАу
- •Метод Эйлера с пересчетом
- •Метод Гаусса-Зейделя
- •Одношаговые методы
- •Решение нелинейных уравнений
- •Многошаговые методы
- •Метод деления отрезка пополам для решения нелинейного уравнения
- •Методы Рунге-Кутта
- •Метод хорд для решения нелинейных уравнений Метод хорд
- •Задача Коши для разрешения обыкновыеннх дифф. Уравнений
- •Метод Ньютона Метод Ньютона (метод касательных)
- •Краевая задача для уравнений
- •2. Теоретическая справка
- •2.1. Пример краевой задачи
- •Метод простой итерации Метод простых итераций
- •Основные понятия метода сеток
- •Комплексные корни
- •Многошаговый метод Адамса
- •Метод простой итерации для решения системы
- •Задача Дирихле для уравнения Лапласа
- •Приближения функции. Аппроксимация.
- •Явные и неявные разностные схемы
- •Явные схемы
- •[Править]Неявные схемы
- •Полунеявные схемы
- •Интерполяция
- •Определения
- •[Править]Пример
- •Интерполяция методом ближайшего соседа
- •[Править]Интерполяция многочленами
- •[Править]Обратное интерполирование (вычисление X при заданном y)
- •[Править]Интерполяция функции нескольких переменных
- •[Править]Другие способы интерполяции
- •Аппроксимация, сходимость, устойчивость разностной схемы
- •1.2.7 Аппроксимация.
- •Линейная интерполяция
- •[Править]Геометрическая интерпретация
- •[Править]Применение
- •Уравнение Пуассона
- •Квадратичная интерполяция
- •Уравнение теплопроводности
Билет 1 _____________________________
Погрешность числа в дискретном представлении
Интерполяционный многочлен в форме Лагранжа
Интерполяционный полином, очевидно, можно построить в форме |
||
|
|
(7) |
где gi(x) - многочлен n-ой степени, обладающий следующим свойством: |
||
|
|
(8) |
Свойством (8), в частности, обладает полином вида: |
||
|
|
(9) |
Тогда: |
|
(10) |
|
где |
(11) |
Выражения (10) и (11) совместно образуют интерполяционную формулу Лагранжа. Отметим, что коэффициенты Лагранжа (9) не зависят от значений интерполируемой функции в узлах. Это существенно снижает вычислительные затраты при интерполировании системы функций на общей сетке. |
||
БИЛЕТ 2_____________________________
Погрешность вычислений
Различают два вида погрешностей - абсолютную и относительную. Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения. Относительная погрешность - это отношение абсолютной погрешности к приближенному значению числа. Таким образом, если a - приближенное значение числа x, то выражения для абсолютной и относительной погрешностей запишутся соответственно в виде
![]()
К сожалению, истинное значение величины x обычно неизвестно. Поэтому приведенные выражения для погрешностей практически не могут быть использованы. Имеется лишь приближенное значение a, и нужно найти его предельную погрешность a, являющуюся верхней оценкой модуля абсолютной погрешности, т.е. xa. В дальнейшем значение a принимается в качестве абсолютной погрешности приближенного числа x. В этом случае истинное значение x находится в интервале (a-a, a+a). Для приближенного числа, полученного в результате округления, абсолютная погрешность a принимается равной половине единицы последнего разряда числа. Например, значение a = 0.734 могло быть получено округлением чисел 0.73441, 073353 и др. При этом x0.0005, и полагаем a= 0.0005. При вычислениях на ЭВМ округления, как правило, не производятся, а цифры, выходящие за разрядную сетку машины, отбрасываются. В этом случае максимально возможная погрешность результата выполнения операции в два раза больше по сравнению со случаем округления. Предельное значение относительной погрешности - отношение предельной абсолютной погрешности к абсолютной величине приближенного числа:
![]() .
.
Например, (-2.3) 0.022 (2.2%). Заметим, что погрешность округляется всегда в сторону увеличения. В данном случае (-2.3) 0.03. Приведенные оценки погрешностей приближенных чисел справедливы, если в записи этих чисел все значащие цифры верные. Вспомним, что значащими цифрами считаются все цифры данного числа начиная с первой ненулевой цифры. Например, в числе 0.037 две значащие цифры: 3 и 7, а в числе 14.80 все четыре цифры значащие. Кроме того, при изменении формы записи числа (например, при записи в форме с плавающей точкой) число значащих цифр не должно меняться, т.е. нужно соблюдать равносильность преобразований. Например, записи 7500 = 0.7500104 и 0.110102 = 11.0 равносильные, а записи 7500 = 0.75104 и 0.110102 = 11 неравносильные. Сформулируем правила оценки предельных погрешностей при выполнении операций над приближенными числами. При сложении или вычитании чисел их абсолютные погрешности складываются. Относительная погрешность суммы заключена между наибольшим и наименьшим значениями относительных погрешностей слагаемых; на практике принимается наибольшее значение. При умножении или делении чисел друг на друга их относительные погрешности складываются. При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени. Для случая двух приближенных чисел a и b эти правила можно записать в виде формул:
![]() ,
,
![]() .
.
Пример1. Найти относительную погрешность функции
 .
.
Используя вышеприведенные формулы, получаем
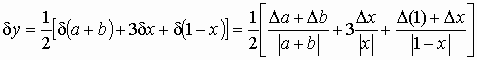 .
.
Полученная оценка относительной погрешности содержит в знаменателе выражение 1-x. Ясно, что при x 1можем получить очень большую погрешность. Поэтому при организации вычислительных алгоритмов следует избегать вычитания близких чисел. При возможности алгоритм нужно видоизменить во избежание потери точности на некотором этапе вычислений. Из рассмотренных правил следует, что при сложении или вычитании приближенных чисел желательно, чтобы эти числа обладали одинаковыми абсолютными погрешностями, т.е. одинаковым числом разрядов после десятичной точки. Например, 38.723 + 4.9 = 43.6; 425.4 - 0.047 = 425.4. Учет отброшенных разрядов не повысит точность результатов. При умножении и делении приближенных чисел количество значащих цифр выравнивается по наименьшему из них. Рассмотрим функцию одной переменной y = f(x). Пусть a - приближенное значение аргумента x, a - его абсолютная погрешность. Абсолютную погрешность функции можно считать ее приращением, которое можно заменить дифференциалом: ydy. Тогда для оценки абсолютной погрешности получим выражение y = f(a)a. Аналогичное выражение можно записать для функции нескольких аргументов.
Погрешности вычислений. Ошибки .
Ошибки.
За исключением возможных промахов (грубых ошибок) в приближенных вычислениях встречаются ошибки начальных данных, ошибки округления, вызванные использованием конечного числа знаков, и ошибки усечения, вызванные конечной аппроксимацией бесконечного процесса. Влияние малых ошибок Δ xi или малых относительных ошибок Δxi/x на результат f(x1, x2, ...) может быть оценено с помощью дифференциала, так
Δ( x1+ x2)=Δx1+Δx2, Δ( x1 x2)=x1Δx2+ x2Δx1,
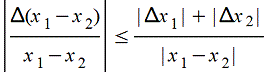
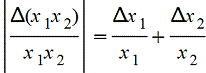 .
.
Возникновение и распространение ошибок в более сложных вычислениях составляют предмет продолжающихся исследований; точные результаты получены лишь в отдельных классах вычислений. Желательно своевременно обнаруживать промахи и ошибки с помощью различных программ контроля. В качестве весьма грубого практического совета можно рекомендовать сохранять на две значащие цифры больше, чем это оправдывается точностью исходных данных или требуемой точностью результата.
Интерполяционный многочлен в форме ньютона
Интерполяционный многочлен легко определяется если его построить в виде: |
||
|
Pn(x) = С0 + С1(x - x0) + C2(x - x0) (x - x1) + ...+ Cn(x - x0)(x - x1) ... (x - xn-1) |
(5) |
Исходя из условия интерполяции (1) для коэффициентов Ci получим систему уравнений треугольного вида |
||
|
f(x0) = С0 f(x1) = С0 + С1(x1 - x0 ) f(x2) = С0 + С1(x1 - x0 ) + C2(x2 - x0 )(x2 - x1 ) . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . f(xn ) = С0 + С1(xn - x0) + C2(xn - x0)(xn - x1) + ...+ Cn(xn - x0)(xn - x1) ... (xn- xn-1) |
|
Из этой системы легко находятся: |
||
|
|
|
Величины, стоящие в правой части приведённых выше равенств, получили название разделённых разностей, соответственно, нулевого, первого и второго порядков. Для них приняты обозначения f[xi], f[xi ,xi-1], f[xi ,xi-1 ,xi-2] и т.д. С учётом этих обозначений выражение (5) можно переписать в виде : |
||
|
Pn(x) = f[x0] + f[x1 ,x0](x - x0) + f[x2 ,x1 ,x0](x - x0)(x - x1) + ... + f[xn ,xn-1 ,...x0](x - x0)(x - x1)...(x - xn-1) |
(6) |
Можно показать, что |
||
|
|
(7) |
Выражения (6) и (7) определяют интерполяционный полином в форме Ньютона. Вычисление полинома в Ньютоновской форме удобно при последовательном дополнении сетки(n+2)-м узлом и наращивании порядка интерполяционного полинома. При этом необходимо вычислить лишь одно дополнительное слагаемое f[xn+1 ,xn,...x0](x - x0)(x - x1)...(x - xn) в выражении (6).
БИЛЕТ 3__________________________________ |
||
Метод прямоугольников для численного интегрирования
Задача численного интегрирования состоит в нахождении приближенного значения интеграла
( 1 )
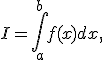
где ![]() -
заданная и интегрируемая на
отрезке
-
заданная и интегрируемая на
отрезке ![]() функция.
функция.
Если
один или оба предела равны ![]() или
или ![]() ,
то с помощью трюков с заменой переменных
можно осуществить переход к конечному
отрезку от луча или всей числовой прямой.
,
то с помощью трюков с заменой переменных
можно осуществить переход к конечному
отрезку от луча или всей числовой прямой.
Введем
на
сетку
с переменным шагом ![]() ,
т.е. множество точек
,
т.е. множество точек  ,
и представим интеграл (1) в
виде суммы интегралов по частичным
отрезкам:
,
и представим интеграл (1) в
виде суммы интегралов по частичным
отрезкам:
( 3 )
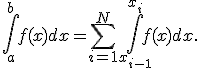
Для построения формулы численного интегрирования на всем отрезке достаточно построить квадратурную формулу для интеграла
( 4 )
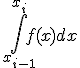
на
частичном отрезке ![]() и
воспользоваться свойством (3).
и
воспользоваться свойством (3).
Метод прямоугольников
Формула прямоугольников на частичном отрезке и ее погрешность
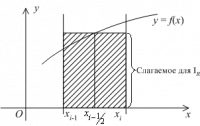
![]()
Рис.2
Заменим
интеграл (3) выражением ![]() ,
где
,
где ![]()
Тогда получим формулу
( 5 )
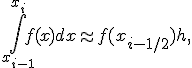
которая
называется формулой
прямоугольников на частичном отрезке ![]()
Погрешность метода (5) определяется величиной

которую
легко оценить с помощью формулы Тейлора.
Действительно, запишем ![]() в
виде
в
виде
( 6 )

и воспользуемся разложением
![]()
где ![]() .
Тогда из (6) получим
.
Тогда из (6) получим
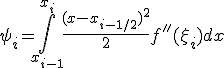
Обозначая ![]() ,
оценим
следующим
образом:
,
оценим
следующим
образом:
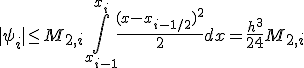
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка
( 7 )
![]()
т.е.
формула имеет погрешность ![]() при
при ![]() .
.
Заметим,что
оценка (7) является
неулучшаемой, т.е. существует функция
,
для которой (7) выполняется
со знаком равенства. Действительно,
для ![]() имеем
имеем ![]() и
и
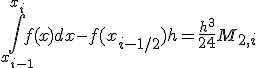
Составная формула прямоугольников и ее погрешность
Суммируя
равенства (5) по ![]() от
от ![]() до
до ![]() ,
получим составную
формулу прямоугольников
,
получим составную
формулу прямоугольников
( 8 )
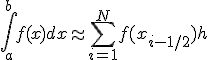
Погрешность этой формулы
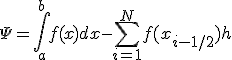
равна сумме погрешностей по всем частичным отрезкам,
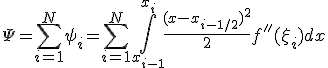
Отсюда,
обозначая ![]() ,
получим
,
получим
( 9 )
![]()
т.е.
погрешность формулы прямоугольников
на всем отрезке есть велицина ![]() .
.
Видим, что квадратурная формула имеет второй порядок точности.
Применимость метода к функции, заданной в конечном числе точек
Заметим, что метод прямоугольников в том виде,в котором он описан выше, не применим в общем случае к функциям,значения которых мы знаем в конечном числе точек, так как, например, мы не всегда можем разбить отрезкок интегрирования на подотрезки, серединами которых являются точки,в которых нам известно значение функции.
Эмпирические формулы. Приближенный метод наименьших квадратов
Общие положения
|
Для упрощения изложения рассмотрим сначала случай линейной функции одного аргумента. Пусть из опыта получены точки: |
x1, y1, |
|
|
x2, y2, ... |
|
(1) |
xn, yn |
|
|
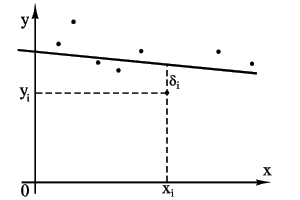
(см. рисунок). Требуется найти уравнение прямой
y=ax+b, |
(2) |
наилучшим образом согласующейся с опытными точками.
Пусть
мы нашли такую прямую. Обозначим
через ![]() расстояние
опытной точки от этой прямой (измеренное
параллельно оси y).
расстояние
опытной точки от этой прямой (измеренное
параллельно оси y).
Из уравнения (2) следует, что
|
(3) |
Чем меньше числа по абсолютной величине, тем лучше подобрана прямая (2). В качестве характеристики точности подбора прямой (2) можно принять сумму квадратов
|
(4) |
Покажем, как можно подобрать прямую (2) так, чтобы сумма квадратов S была минимальной. Из уравнений (3) и (4) получаем
|
(5) |
Условия минимума S будут
|
(6) |
|
(7) |
Уравнения (6) и (7) можно записать в таком виде:
|
(8) |
|
(9) |
Из уравнений (8) и (9) легко найти a и b по опытным значениям xi и yi. Прямая (2), определяемая уравнениями (8) и (9), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (8) и (9), из которых определяется прямая (2), называются нормальными уравнениями.
Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки (1) и уравнение (2), можно записать систему уравнений для a и b
y1=ax1+b, |
|
|
y2=ax2+b, ... |
|
(10) |
yn=axn+b, |
|
|
Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т.е. на x1, x2, ..., xn) и сложим полученные уравнения, в результате получится первое нормальное уравнение (8).
Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т.е. на 1, и сложим полученные уравнения, в результате получится второе нормальное уравнение (9).
Этот способ получения нормальных уравнений является общим: он пригоден, например, и для функции
y=a0+a1x+a2x2+...+anxn. |
(11) |
Естественно, что здесь получится система из n+1 нормального уравнения для определения величин a0, a1, a2, ..., an.
Рассмотрим частный случай применения метода наименьших квадратов. Пусть из теории известно, что
k=y/x |
(12) |
есть величина постоянная и ее нужно определить по опытным данным (1).
Систему уравнений для k можно записать:
k=y1/x1, |
|
|
k=y2/x2, ... |
|
(13) |
k=yn/xn, |
|
|
Для получения нормального уравнения умножим каждое из этих уравнений на коэффициент при неизвестной k, т.е. на 1, и сложим полученные уравнения
|
(14) |
отсюда
|
(15) |
Следовательно, среднее арифметическое, полученное из опытных отношений yi/xi, дает решение поставленной задачи по методу наименьших квадратов. Это важное свойство средней арифметической объясняет ее широкое применение в практике обработки опытных данных.
БИЛЕТ 4_______________________________
Метод трапеций для численного интегрирования
Формула трапеций на частичном отрезке и ее погрешность

Рис.3
На частичном отрезке эта формула имеет вид
( 10 )
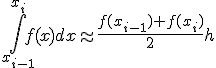
и
получается путем замены подынтегральной
функции
интерполяционным
многочленом первой степени,постоенным
по узлам ![]() ,
т.е. функцией
,
т.е. функцией
![]()
Для оценки погрешности достаточно вспомнить,что
![]()
Отсюда получим
и,следовательно,
( 11 )
![]()
Оценка (11) неулучшаема,
так как в ней достигается равенство,
например, для ![]() .
.
Составная формула трапеций и ее погрешность
Составная формула трапеций имеет вид
( 12 )

где ![]() .
.
Погрешность этой формулы оценивается следующим образом:
( 13 )
![]()
где
Таким
образом, формула трапеций имеет, так же
как и формула прямоугольников, второй
порядок точности,![]() ,
но ее погрешность оценивается величиной
в два раза большей.
,
но ее погрешность оценивается величиной
в два раза большей.
Применимость метода к функции, заданной в конечном числе точек
В отличие от метода прямоугольников, метод трапеций применим к функциям, заданным в конечном числе точек, так как мы всегда можем взять в качесве узлов интегрирования данные точки.
БИЛЕТ 5______________________________
Метод Симпсона
При
интегрировании по методу Симпсона
подынтегральная кривая представляется
в виде кусочно-непрерывной функцией
представляющей отрезки квадратичных
парабол, т. е. интерполяционным полиномом
2-й степени (рис. 15.3). При этом интервал
(a,
b)
разбивают на 2n частей
с шагом ![]() Формула
цифрового интегрирования по методу
Симпсона имеет вид:
Формула
цифрового интегрирования по методу
Симпсона имеет вид:
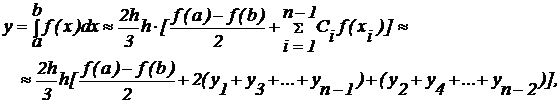 при
этом:
при
этом: ![]() ;
;  Интегрирование
осуществляется путем суммирования
элементарных площадей
Интегрирование
осуществляется путем суммирования
элементарных площадей  под
кривой подынтегральной функции
под
кривой подынтегральной функции ![]() на
интервале (a,
b)
на
интервале (a,
b)
Метод Симпсона обеспечивает большую точность вычисления по сравнению с методом прямоугольников и трапеций.
Рис. 14.3. Интегрирование по методу трапеций
Интерполяция сплайнами
Интерполяционные
формулы Лагранжа, Ньютона и Стирлинга
и др. при использовании большого числа
узлов интерполяции на всем отрезке
[a, b]
часто приводят к плохому приближению
из-за накопления погрешностей в процессе
вычислений [2]. Кроме того, из-за расходимости
процесса интерполяции увеличение числа
узлов не обязательно приводит к повышению
точности. Для снижения погрешностей
весь отрезок [a, b]
разбивается на частичные отрезки и на
каждом из них функцию![]() заменяют
приближенно полиномом невысокой степени.
Это называется кусочно-полиномиальной
интерполяцией.
заменяют
приближенно полиномом невысокой степени.
Это называется кусочно-полиномиальной
интерполяцией.
Один из способов интерполирования на всем отрезке [a, b] является интерполирование сплайнами.
Сплайном называется кусочно-полиномиальная функция, определенная наотрезке [a, b] и имеющая на этом отрезке некоторое количество непрерывных производных. Преимущества интерполяции сплайнами по сравнению с обычными методами интерполяции – в сходимости и устойчивости вычислительного процесса.
Рассмотрим один из наиболее распространенных в практике случаев – интерполирование функции кубическим сплайном. Пусть на отрезке [a, b] задана непрерывная функция . Введем разбиение отрезка:
![]() (6)
(6)
и
обозначим ![]() ,
, ![]() .
.
Сплайном,
соответствующим данной функции
и
узлам интерполяции (6) называется
функция ![]() ,
удовлетворяющая следующим условиям:
,
удовлетворяющая следующим условиям:
1)
на каждом отрезке ![]() ,
,![]() функция
является
кубическим многочленом;
функция
является
кубическим многочленом;
2) функция , а также ее первая и вторая производные непрерывны на отрезке [a, b] ;
3) ![]()
Третье условие называется условием интерполирования. Сплайн, определяемый условиями 1) – 3), называется интерполяционным кубическим сплайном.
Рассмотрим способ построения кубического сплайна [2].
На
каждом из отрезков
,
будем
искать сплайн-функцию ![]() в
виде полинома третьей степени:
в
виде полинома третьей степени:
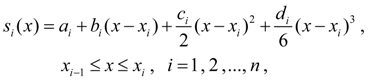 (7)
(7)
где ![]() искомые
коэффициенты.
искомые
коэффициенты.
Продифференцируем (7) трижды по х :
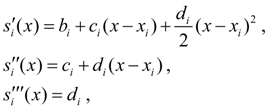
откуда следует
![]()
Из условия интерполирования 3) получаем:
![]() . (8)
. (8)
Кроме
того, будем считать ![]() .
.
Из условий непрерывности функции вытекает:
![]()
Отсюда с учетом (7) получим:
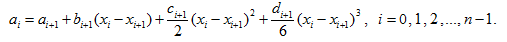
Обозначив![]() и
опуская промежуточные выкладки [2],
окончательно получим систему уравнений
для определения коэффициентов
и
опуская промежуточные выкладки [2],
окончательно получим систему уравнений
для определения коэффициентов![]() :
:
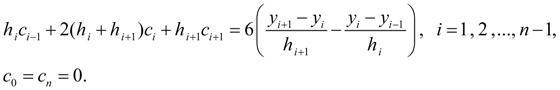 (9)
(9)
В силу трехдиагональности матрицы коэффициентов система (9) имеет единственное решение [2]. Найдя коэффициенты , остальные коэффициенты определим по явным формулам:
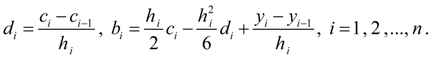 (10)
(10)
Таким образом, существует и найден единственный кубический сплайн, удовлетворяющий условиям 1) – 3) .
БИЛЕТ 6 _____________________________________
Способы численного интегрирования несобственными интегралами
Аппроксипация производных
Напомним, что производной функции y=f(x) называется предел отношения приращения функции D y к приращению аргумента D x при стремлении D x к нулю:
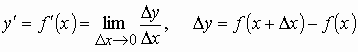 . (1)
. (1)
Обычно для вычисления производных используют готовые формулы (таблицу производных) и к выражению (1) не прибегают. Однако в численных расчетах на ЭВМ использование этих формул не всегда удобно и возможно. В частности, функция y=f(x) может быть задана в виде таблицы значений. В таких случаях производную находят, опираясь на формулу (1). Значение шага D x полагают равным некоторому конечному числу и для вычисления значения производной получают приближенное равенство
![]() . (2)
. (2)
Это соотношение называется аппроксимацией (приближением) производной с помощью отношения конечных разностей (значения D y, D x в формуле (2) конечные в отличие от их бесконечно малых значений в (1)).
Рассмотрим
аппроксимацию производной для
функции y=f(x),
заданной в табличном
виде: y0, y1,… при x =x0, x1,…. Пусть шаг -
разность между соседними значениями
аргумента - постоянный и равен h.
Запишем выражения для производной ![]() при x = x1.
В зависимости от способа вычисления
конечных разностей получаем разные
формулы для вычисления производной в
одной и той же точке:
при x = x1.
В зависимости от способа вычисления
конечных разностей получаем разные
формулы для вычисления производной в
одной и той же точке:
![]() (3)
(3)
с помощью левых разностей;
![]() (4)
(4)
с помощью правых разностей;
![]() (5)
(5)
с помощью центральных разностей.
Можно найти также выражения для старших производных. Например,
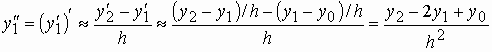 . (6)
. (6)
Таким образом, по формуле (2) можно найти приближенные значения производных любого порядка. Однако при этом остается открытым вопрос о точности полученных значений.
БИЛЕТ 7_______________________________
Классификация методов решения слау
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
|
(1) |

![]()
Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.
Здесь ![]() —
количество уравнений, а
—
количество уравнений, а ![]() —
количество неизвестных. x1, x2,
…, xn — неизвестные,
которые надо определить. a11, a12,
…, amn — коэффициенты
системы — и b1, b2,
… bm — свободные
члены — предполагаются известными[1].
Индексы коэффициентов (aij)
системы обозначают номера уравнения
(i) и неизвестного (j), при котором
стоит этот коэффициент, соответственно[2].
—
количество неизвестных. x1, x2,
…, xn — неизвестные,
которые надо определить. a11, a12,
…, amn — коэффициенты
системы — и b1, b2,
… bm — свободные
члены — предполагаются известными[1].
Индексы коэффициентов (aij)
системы обозначают номера уравнения
(i) и неизвестного (j), при котором
стоит этот коэффициент, соответственно[2].
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
Прямые (или точные) методы позволяют найти решение за определённое количество шагов. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.
[Править]Прямые методы
Метод Гаусса
Метод Гаусса — Жордана
Метод Крамера
Матричный метод
Метод прогонки (для трёхдиагональных матриц)
Разложение Холецкого или метод квадратных корней (для положительно-определённых симметричных и эрмитовых матриц)
Метод вращений[3]
[Править]Итерационные методы
Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения
![]() ,
,
эквивалентного
начальной системе линейных алгебраических
уравнений. При итерации ![]() в
правой части уравнения заменяется,
например, в методе Якоби (метод простой
итерации) приближение, найденное на
предыдущем шаге:
в
правой части уравнения заменяется,
например, в методе Якоби (метод простой
итерации) приближение, найденное на
предыдущем шаге:
![]() .
.
Среди итерационных методов можно отметить самые популярные:
Метод Якоби (метод простой итерации)[источник не указан 28 дней]
Метод Гаусса — Зейделя
Метод релаксации
Многосеточный метод
Метод Монтанте
Метод Абрамова (пригоден для решения небольших СЛАУ)
Метод обобщённых минимальных невязок (англ.)
Метод бисопряжённых градиентов (англ.)
Стабилизированный метод бисопряжённых градиентов (англ.)
Квадратичный метод сопряжённых градиентов (англ.)
Метод квази-минимальных невязок (QMR)

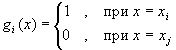 для (i,j)
= 0,1,...,n ,
для (i,j)
= 0,1,...,n , 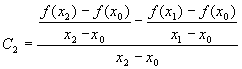 и
так далее.
и
так далее.