
- •Список вопросов по курсу математического анализа, 4 семестр
- •Функционал. Линейное нормированное пространство. Метрическое пространство. Топологическое пространство.
- •Вопрос 8. Определение метрического пространства. Примеры
- •Вопрос 9. Расстояния на множестве непрерывных функций
- •Вопрос 10. Сходимость в метрическом пространстве
- •Вопрос 11. Равномерная сходимость и сходимость в среднем
- •Вопрос 12. Замкнутые множества в метрическом пространстве, их свойства
- •Вопрос 13. Замыкание множества в метрическом пространстве
- •Вопрос 14. Открытые множества в метрическом пространстве
- •Вопрос 15. Полные метрические пространства
- •Вопрос 16.Примеры полных метрических пространств.
- •Вопрос 17. Топологические пространства
- •Вопрос 20. Пространство . Компактные множества в
- •Открытые и закрытые множества в .
- •Сходимость в .
- •Компактные множества в .
- •Вопрос 21. Непрерывные функции и отображения
- •Вопрос 22. Индуцированная топология . Теоремы о максимуме
- •Раздел 12. Элементы вариационного исчисления
Раздел 12. Элементы вариационного исчисления
Излагаются основы вариационного исчисления
Рассматривается уравнение Эйлера, условия трансверсальности
ВВЕДЕНИЕ
Рассмотрим
следующую задачу, представляющую собой
модель некоторого экономического
исследования. Пусть функции
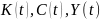 определены на отрезке
определены на отрезке
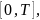 функция
функция
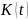 дифференцируема
на этом отрезке. Считаем заданными
величины
дифференцируема
на этом отрезке. Считаем заданными
величины
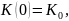
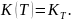 Отметим,
что задание функции
Отметим,
что задание функции
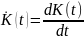 определяет саму функцию
ввиду равенства
определяет саму функцию
ввиду равенства
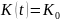 +
+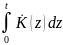 .
.
Пусть
функция
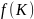 определена на множестве, содержащем
множество значений функции
на отрезке
определена на множестве, содержащем
множество значений функции
на отрезке
 .
Пусть она дважды дифференцируема и
пусть
.
Пусть она дважды дифференцируема и
пусть
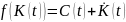 .
(1)
.
(1)
Кроме
того, пусть для всех
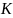 выполняются неравенства
выполняются неравенства
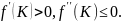
Уравнение
(1) показывает, что функции
и
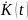 определяют функцию
определяют функцию
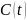 .
.
Пусть
функция
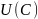 определена на множестве, содержащем
множество значений функции
на отрезке
.
Пусть она дважды дифференцируема и для
всех
определена на множестве, содержащем
множество значений функции
на отрезке
.
Пусть она дважды дифференцируема и для
всех
 выполняются неравенства
выполняются неравенства
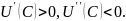
Пусть
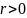 .
Интерес представляет величина
.
Интерес представляет величина
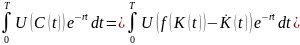
и
задача состоит в том, чтобы за счёт
выбора функции
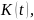
 удовлетворяющей
условиям
удовлетворяющей
условиям
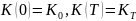 добиться наибольшего возможного значения
этого интеграла.
добиться наибольшего возможного значения
этого интеграла.
Рассмотренная
задача представляет собой пример так
называемой простейшей
задачи вариационного исчисления,
которая формулируется следующим образом.
Рассматривается отрезок
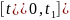 и дифференцируемые функции
и дифференцируемые функции
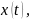 удовлетворяющие условиям
удовлетворяющие условиям
 )=
)=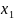 ,
а также функция
,
а также функция
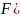 ),
обладаюшая определёнными свойствами,
которые будут уточнены ниже. Ищется
),
обладаюшая определёнными свойствами,
которые будут уточнены ниже. Ищется
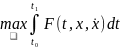
по всем дифференцируемым функциям удовлетворяющим условиям )= .
Отметим
очевидное сходство этой задачи с задачей
отыскания наибольшего значения функции
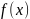 на отрезке
на отрезке
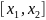 . Отметим и очевидное различие: в задаче
об отыскании экстремума функции
отыскивается точка. В поставленной выше
задаче отыскивается функция.
. Отметим и очевидное различие: в задаче
об отыскании экстремума функции
отыскивается точка. В поставленной выше
задаче отыскивается функция.
Следующий параграф как раз и посвящён соображениям, позволяющим более явно увидеть это сходство и уменьшить различие.
ФУНКЦИОНАЛ. ФУНКЦИОНАЛЬНОЕ ПРОСТРАНСТВО
Определение.
Если
каждой функции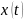 из некоторого множества функций
из некоторого множества функций
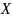 поставлено в соответствие число
поставлено в соответствие число
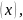 то говорят, что на этом множестве
определён функционал.
то говорят, что на этом множестве
определён функционал.
Примеры:
Зафиксируем точку
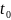 и рассмотрим множество
функций
,
определённых в этой точке. Определим
функционал
и рассмотрим множество
функций
,
определённых в этой точке. Определим
функционал
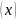 равенством
равенством
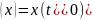 .
.Зафиксируем точку и рассмотрим множество функций , дифференцируемых в этой точке. Определим функционал равенством
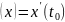 .
.Рассмотрим класс функций , интегрируемых на отрезке
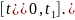 Определим функционал
равенством
Определим функционал
равенством

Введённая выше для непрерывной по совокупности переменных функции ) величина
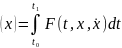
является
функционалом на множестве
функций
,
имеющих на отрезке
непрерывную производную
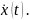
Замечание. Рассмотренные в примерах 3 и 4 функционалы обладают так называемым свойством локальности. Это свойство состоит в том, что если разбить отрезок на части, вычислить значения функционала на этих частях и взять сумму этих значений, то эта сумма окажется равной значению функционала на всём отрезке. Далеко не все функционалы обладают этим свойством. Например, функционал

Представляющий собой абсциссу центра тяжести материальной кривой, свойством локальности не обладает.
При
изучении теории функций от
переменных было удобно пользоваться
геометрическим языком, рассматривая
набор чисел
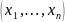 как
точку
как
точку
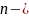 мерного пространства
.
В этом пространстве вводились понятия
нормы вектора
мерного пространства
.
В этом пространстве вводились понятия
нормы вектора
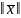 =
=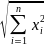
и расстояния между точками
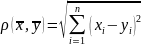 .
.
При этом
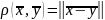 .
.
При
исследовании задач вариационного
исчисления также очень полезен
геометрический язык, при пользовании
которым мы рассматриваем функцию
,
как точку некоторого функционального
пространства. В обычном
мерном анализе рассматривались функции,
определённые на подмножествах одного
и того же пространства
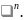 В задачах вариационного исчисления
такого универсального пространства
нет, рассматриваемое функциональное
пространство выбирается в зависимости
от класса решаемых задач.
В задачах вариационного исчисления
такого универсального пространства
нет, рассматриваемое функциональное
пространство выбирается в зависимости
от класса решаемых задач.
Определение.
Линейным
нормированным пространством
называется линейное(векторное)
пространство
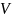 ,
каждому элементу
,
каждому элементу
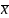 которого поставлено в соответствие
неотрицательное число
которого поставлено в соответствие
неотрицательное число
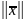 ,
называемое нормой
этого элемента. При этом норма обладает
следующими свойствами (аксиомы нормы):
,
называемое нормой
этого элемента. При этом норма обладает
следующими свойствами (аксиомы нормы):
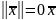 =
=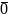 .
.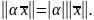 (2)
(2)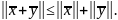
В
линейном нормированном пространстве
можно ввести метрику
(или, что то же самое, расстояние), положив
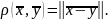 Таким образом, линейное нормированное
пространство представляет собой
метрическое пространство. Следует
отметить, что элементами линейного
нормированного пространства могут быть
объекты различной природы: числа,
векторы, матрицы, функции и т.д.
Таким образом, линейное нормированное
пространство представляет собой
метрическое пространство. Следует
отметить, что элементами линейного
нормированного пространства могут быть
объекты различной природы: числа,
векторы, матрицы, функции и т.д.
Мы будем, в основном, рассматривать следующие пространства.
Определение.
Пространство
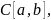 которое
состоит из непрерывных на отрезке
которое
состоит из непрерывных на отрезке
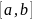 функций.
Норма в этом пространстве определена
равенством
функций.
Норма в этом пространстве определена
равенством
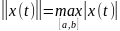 .
(3)
.
(3)
Расстояние между его элементами равно
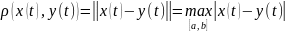 .
(4)
.
(4)
Определение.
Пространство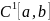 , которое состоит из непрерывных на
отрезке
функций
, которое состоит из непрерывных на
отрезке
функций
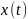 ,
обладающих непрерывной на этом отрезке
производной
,
обладающих непрерывной на этом отрезке
производной
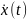 .
Норма в этом пространстве определяется
равенством
.
Норма в этом пространстве определяется
равенством
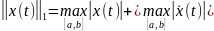 ,
(5)
,
(5)
а расстояние, соответственно, равенством
 .
(6)
.
(6)
Определение.
Пространство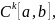 которое состоит из непрерывных на
отрезке
функций
,
обладающих на этом отрезке непрерывными
производными до порядка
которое состоит из непрерывных на
отрезке
функций
,
обладающих на этом отрезке непрерывными
производными до порядка
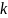 включительно.
Норма в этом пространстве определяется
равенством
включительно.
Норма в этом пространстве определяется
равенством
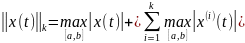 (7)
(7)
а расстояние, соответственно, равенством
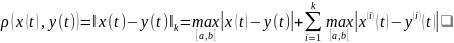 .(8)
.(8)
Задача. Проверить, что определённые равенствами (3),(5), (7) величины удовлетворяют аксиомам нормы.
НЕПРЕРЫВНОСТЬ ФУНКЦИОНАЛА
Пусть
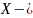 функциональное
пространство, обладающее структурой
линейного нормированного пространства
( иными словами, в нём введена некоторая
норма).
функциональное
пространство, обладающее структурой
линейного нормированного пространства
( иными словами, в нём введена некоторая
норма).
Определение.
Функционал
называется непрерывным
в точке
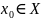 ,
если для любого
,
если для любого
 существует число
существует число
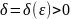 такое, что для всех
такое, что для всех
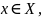 удовлетворяющих неравенству
удовлетворяющих неравенству
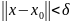 выполняется неравенство
выполняется неравенство
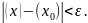
Замечание. Непрерывность функционала представляет собой свойство, зависящее от того, в каком пространстве рассматривается исследуемый функционал.
Например, интересующий нас функционал
в
случае непрерывной по совокупности
переменных
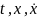 функции
)
непрерывен в пространстве
функции
)
непрерывен в пространстве
 и не является, вообще говоря, непрерывным,
если рассматривать его
и не является, вообще говоря, непрерывным,
если рассматривать его
на
множестве
функций
,
имеющих на отрезке
непрерывную производную
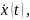 но при этом понимать близость таких
функций в смысле нормы пространства
но при этом понимать близость таких
функций в смысле нормы пространства
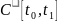 .
.
Типичным примером такой ситуации является функционал
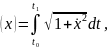
представляющий
собой длину гладкой кривой, соединяющей
точки
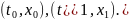 Этот функционал непрерывен, если
рассматривать его в метрике пространства
,
но не является непрерывным, если
рассматривать его в метрике пространства
.
Действительно, производные близких
друг другу функций могут значительно
отличаться друг от друга и длины
соответствующих кривых также могут
значительно отличаться друг от друга.
Этот функционал непрерывен, если
рассматривать его в метрике пространства
,
но не является непрерывным, если
рассматривать его в метрике пространства
.
Действительно, производные близких
друг другу функций могут значительно
отличаться друг от друга и длины
соответствующих кривых также могут
значительно отличаться друг от друга.
ВАРИАЦИЯ ФУНКЦИОНАЛА
При исследовании обычных функций на экстремум важную роль играло понятие дифференциала – главной линейной части приращения функции. Аналогом этого понятия
служит определяемое ниже понятие вариации функционала.
Определение.
Пусть
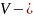 линейное нормированное пространство
и
линейное нормированное пространство
и
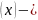 функционал,
определённый на этом пространстве. Он
называется линейным,
если он непрерывен и если для любых
функционал,
определённый на этом пространстве. Он
называется линейным,
если он непрерывен и если для любых
 выполняется равенство
выполняется равенство
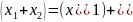 (
(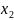 ).
).
Все функционалы из примеров 1-4 пункта линейные.
Рассмотрим теперь функционал и его приращение
 (x),
(x), (9)
(9)
При
фиксированном
 величина (9) представляет собой функционал(
в общем случае, нелинейный) от переменной
величина (9) представляет собой функционал(
в общем случае, нелинейный) от переменной
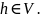
Определение.
Вариацией
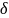 (или
дифференциалом ) функционала
называется линейный функционал
(или
дифференциалом ) функционала
называется линейный функционал
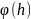 ,
для которого
,
для которого
(x)=
+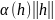 ,
(10)
,
(10)
где
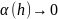 при
при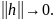
Заметим, что определение (10) вариации функционала вполне аналогично определению дифференциала дифференцируемой функции.
Теорема. Если вариация функционала существует, то она определяется однозначно.
Лемма.
Если
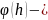 линейный
функционал, для которого
линейный
функционал, для которого
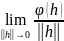 =0,
(11)
=0,
(11)
то
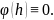
Предположим,
что утверждение леммы неверно и что при
условии (11) всё же существует элемент
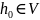 такой, что
такой, что
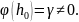 Положим
Положим
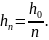 Тогда, по свойству нормы,
Тогда, по свойству нормы,
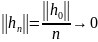 ,
,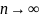 .
Однако
.
Однако и
и
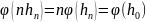 ,
откуда
,
откуда
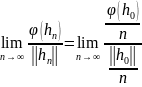 =
=
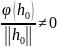 .
.
Полученное противоречие доказывает лемму.
Вернёмся к доказательству теоремы и предположим, что
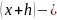 (x)=
(x)=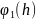 +
+ ,
,
(x)=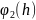 +
+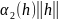 .
.
Тогда линейный функционал
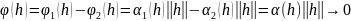 при
при
По
лемме
 что означает, что
что означает, что
 ,
что и требовалось доказать.
,
что и требовалось доказать.
Пример. Найти приращение функционала
 ,
,
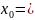 t
t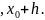
Решение.
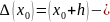 (
(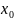 )=
)=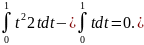
Пример. Найти вариацию функционала
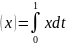 .
.
Решение.
(x)=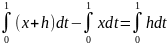 .
.
Правая
часть этого равенства представляет
собой линейный относительно
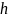 функционал и, следовательно, он и
является искомой вариацией.
функционал и, следовательно, он и
является искомой вариацией.
Формула для вычисления вариации функционала более общего вида
будет получена, при естественных условиях, ниже в равенстве (17).
ЭКСТРЕМУМ ФУНКЦИОНАЛА
Напомним,
что функция
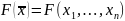 имеет в точке
имеет в точке
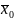 максимум(минимум), если существует
окрестность этой точки такая, что для
всех
из этой окрестности приращение этой
функции
максимум(минимум), если существует
окрестность этой точки такая, что для
всех
из этой окрестности приращение этой
функции
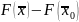 меньше,
или равно 0( для минимума – больше, или
равно). В случае строгого максимума или
минимума неравенства тоже строгие.
меньше,
или равно 0( для минимума – больше, или
равно). В случае строгого максимума или
минимума неравенства тоже строгие.
Вполне
аналогично можно говорить, что функционал
имеет
экстремум в точке
,
если его приращение сохраняет знак в
некоторой окрестности точки
.
Однако, как отмечалось выше, понятие
окрестности зависит от нормы
рассматриваемого пространства. Поскольку
в дальнейшем рассматриваются функционалы,
определённые на некотором множестве
непрерывно дифференцируемых функций,
сами эти функции можно рассматривать
либо как элементы пространства
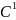 ,
либо как элементы пространства
.
,
либо как элементы пространства
.
В первом случае, т.е. если окрестность рассматривается в пространстве , говорят о слабом экстремуме функционала.
Во втором случае, т.е. если окрестность рассматривается в пространстве , говорят о сильном экстремуме функционала.
Ясно, что точка сильного экстремума функционала является и точкой слабого экстремума функционала, поскольку окрестность точки в пространстве входит и в некоторую окрестность этой точки в пространстве . Обратное, в общем случае, неверно.
Обычно задача отыскания слабого экстремума проще, чем задача отыскания сильного экстремума, так как рассматриваемые функционалы обычно непрерывны в , но не непрерывны в .
Теорема. (Необходимое условие экстремума функционала). Если имеет экстремум в точке и если в этой точке существует его вариация , то она равна 0.
Рассмотрим, для определённости, случай минимума, т.е. пусть
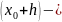 (
)
(
)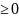
для
всех с достаточно малой величиной 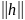 .
По определению вариации,
.
По определению вариации,
(
)=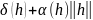 ,
(12)
,
(12)
где
при
Если
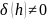 ,
то при достаточно малых
знак правой части равенства (12) определяется
знаком
,
то при достаточно малых
знак правой части равенства (12) определяется
знаком
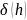 .
Но
.
Но
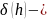 линейный функционал, поэтому
линейный функционал, поэтому
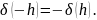
Следовательно, приращение ( ) меняет свой знак в окрестности точки и в ней нет экстремума функционала .
Замечание. Обратите внимание на аналогию между этой теоремой и теоремой о необходимом условии экстремума функции( теоремой Ферма).
УРАВНЕНИЕ ЭЙЛЕРА
Пусть
функция
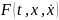 имеет
непрерывные частные производные по
всем переменным до второго порядка
включительно. Поставим задачу найти
среди функций
,
имеющих на отрезке
непрерывную производную
имеет
непрерывные частные производные по
всем переменным до второго порядка
включительно. Поставим задачу найти
среди функций
,
имеющих на отрезке
непрерывную производную
 и удовлетворяющих условиям
и удовлетворяющих условиям
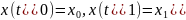 (13)
(13)
такую, которая является точкой слабого экстремума функционала
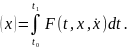 (14)
(14)
Дадим
функции
приращение
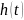 ,
имеющее на отрезке
непрерывную производную. Для того, чтобы
функция
,
имеющее на отрезке
непрерывную производную. Для того, чтобы
функция
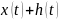 удовлетворяла условиям (13), функция
удовлетворяла условиям (13), функция
должна удовлетворять условиям
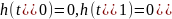 .
(15)
.
(15)
Вычислим
вариацию функционала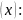
 (x)=
(x)= =
=
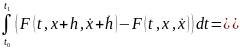
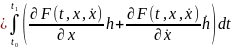 +…
. (16)
+…
. (16)
При
выводе формулы мы воспользовались
разложением по формуле Тейлора, многоточие
означает члены, имеющие степени не ниже
второй по совокупности переменных
Из формулы (16) следует, что величина

представляет
собой главную, линейную по совокупности
переменных
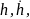 часть
приращения
(x),
т.е. вариацию
функционала
.
Итак,
часть
приращения
(x),
т.е. вариацию
функционала
.
Итак,
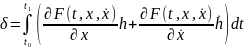 .(17)
.(17)
Докажем основную для дальнейшего теорему.
Теорема. Пусть функция имеет непрерывные частные производные по всем переменным до второго порядка включительно. Для того, чтобы функционал
,
определённый на функций , имеющих на отрезке непрерывную производную и удовлетворяющих условиям достигал слабого экстремума на функции необходимо, чтобы эта функция удовлетворяла уравнению Эйлера:
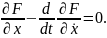 (18)
(18)
Доказательство теоремы базируется на следующей лемме.
Лемма.
(Дюбуа-Реймон).
Если
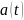 и
и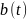 непрерывные функции и если
непрерывные функции и если
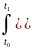 (19)
(19)
для
любой функции
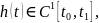 удовлетворяющей
условиям
(15), то
удовлетворяющей
условиям
(15), то
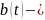 дифференцируемая
функция и
дифференцируемая
функция и
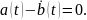
Полное доказательство леммы Дюбуа-Реймона можно найти, например, в книге[], (глава1, параграф 3, лемма 2). Здесь мы ограничимся её частным случаем, являющимся прекрасной иллюстрацией основной идеи. Именно, докажем, что:
если
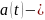 непрерывная
функция
и если для
любой функции
удовлетворяющей
условиям
(15) выполняется
равенство
непрерывная
функция
и если для
любой функции
удовлетворяющей
условиям
(15) выполняется
равенство
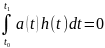 ,
(20)
,
(20)
то
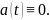
Предположим
противное, т.е. что существует точка
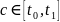 такая, что
такая, что
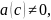
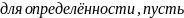
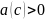 .
Ввиду непрерывности функции
,
существует интервал
.
Ввиду непрерывности функции
,
существует интервал
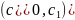 ,
на котором
,
на котором
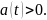 Рассмотрим функцию
Рассмотрим функцию
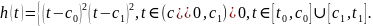
Эта функция принадлежит классу и удовлетворяет условиям (15). Кроме того,

и
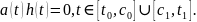
Поэтому
 ,
,
что противоречит условию (20).
Вернёмся к доказательству теоремы и применим лемму, согласно которой
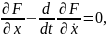
что и требовалось доказать.
Замечание. Уравнение (18) даёт необходимое, но не достаточное условие экстремума функционала. Однако часто бывает очевидно, что решение задачи должно существовать. Если, при этом, уравнение (20) даёт единственное решение, удовлетворяющее условиям (13), то это решение и является искомым.
Часто
в качестве достаточного условия наличия
максимума функционала (14) фигурирует
выпуклость вверх функции
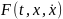 по переменным
по переменным
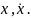 Для наличия минимума этого функционала
достаточна выпуклость вниз
по переменным
Для наличия минимума этого функционала
достаточна выпуклость вниз
по переменным
Определение. Функции, являющиеся решениями уравнения Эйлера (18), называются экстремалями.
Определение. Функции, являющиеся решениями уравнения Эйлера (18) и удовлетворяющие условиям (13), называются допустимыми экстремалями.
Замечание.
Можно
преобразовать уравнение Эйлера, вычисляя
в нём производную по
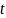 :
:
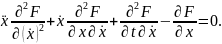 (21)
(21)
Пример. Рассмотрим функционал

и
найдём его допустимые экстремали при
условиях
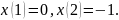
Решение.
Функция
равна
 и уравнение Эйлера имеет вид:
и уравнение Эйлера имеет вид:
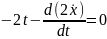 ,
,
или
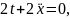 т.е.
т.е.
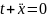 .
Это – линейное уравнение, решением
которого является функция
.
Это – линейное уравнение, решением
которого является функция
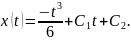
Граничное
условие
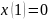 даёт уравнение
даёт уравнение
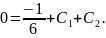
Граничное
условие
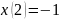 даёт уравнение
даёт уравнение
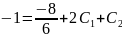 .
.
Из
этих уравнений находим, что
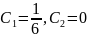 .
Поэтому единственной допустимой
экстремалью является функция
.
Поэтому единственной допустимой
экстремалью является функция
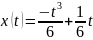 .
.
Задача отыскания экстремума функционала может и не иметь решения. Рассмотрим пример.
Пример. Исследовать на наличие экстремума функционал
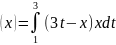
при
условиях
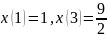 .
.
Решение. Уравнение Эйлера имеет вид:
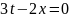 ,
,
откуда
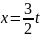
и
при
 условие
условие
 не выполняется.
не выполняется.
Допустимых экстремалей может оказаться и бесконечное множество.
Пример. Исследовать на экстремум функционал

при
условиях
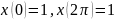 .
.
Решение. Уравнение Эйлера имеет вид:
 ,
,
или.
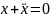 .
Это – линейное уравнение, решением
которого являются функции
.
Это – линейное уравнение, решением
которого являются функции
 .
.
Условия
дают одно и то же уравнение
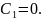 Следовательно, допустимой экстремалью
является любая функция вида
Следовательно, допустимой экстремалью
является любая функция вида
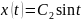 .
.
Как отмечено выше, уравнение Эйлера (18) сводится к уравнению второго порядка (20). Рассмотрим простейшие случаи его интегрируемости.
В
первом из них функция
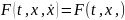 ,
т.е. не зависит от
,
т.е. не зависит от
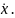 Уравнение Эйлера принимает вид
Уравнение Эйлера принимает вид
 .
.
Это не дифференциальное уравнение. Его решения, как в рассмотренном выше примере, могут и не удовлетворять условиям задачи.
Во
втором случае ,
т.е. зависит только от
Уравнение Эйлера принимает вид
,
т.е. зависит только от
Уравнение Эйлера принимает вид

Его
решениями являются функции
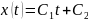 .
.
В
третьем случае
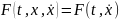 .
Уравнение Эйлера принимает вид
.
Уравнение Эйлера принимает вид
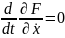 .
.
Оно равносильно совокупности уравнений первого порядка
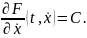
В
четвёртом случае
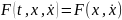 .
Уравнение Эйлера принимает вид
.
Уравнение Эйлера принимает вид

Умножим
обе части этого уравнения на
 и
получим уравнение
и
получим уравнение
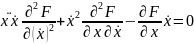 .
.
Его можно преобразовать к виду
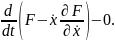
Полученное уравнение равносильно совокупности уравнений первого порядка
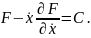
УРАВНЕНИЕ ЭЙЛЕРА ДЛЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ РАМСЕЯ
Рассмотрим задачу нахождения
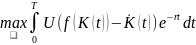 (22)
(22)
при условиях .
Величина определяется равенством
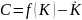 .
(23)
.
(23)
Требуется
также найти
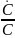 .
.
Решение. Имеем .
Следовательно,
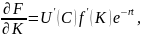
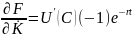 .
.
Уравнение Эйлера имеет вид
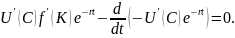 (24)
(24)
Вычислим отдельно
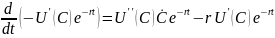
и
подставим в (24). Кроме того, сократим
общий, не равный 0 множитель
 и получим искомое уравнение
и получим искомое уравнение
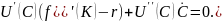 (25)
(25)
Из него находим
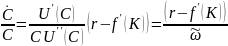 (26)
(26)
Величина
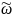 равна
равна
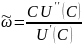 =
=
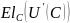 .
.
Предполагая,
что
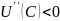 и
и
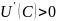 получаем, что
получаем, что
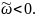 ( В практических расчётах для величины
часто
принимают оценку
( В практических расчётах для величины
часто
принимают оценку
 ).
).
Кроме того, из равенства (26) вытекает, что
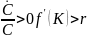 .
.
Из уравнений (25) и (23) получаем
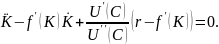 (27)
(27)
При
условии
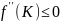 функция
функция
 выпукла
вверх, как функция от переменных
выпукла
вверх, как функция от переменных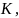
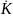 .
Так как
и
,
функция
.
Так как
и
,
функция
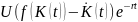 выпукла вверх, как функция от переменных
.
Поэтому любое решение (27), удовлетворяющее
условиям
,
даёт решение поставленной задачи.
выпукла вверх, как функция от переменных
.
Поэтому любое решение (27), удовлетворяющее
условиям
,
даёт решение поставленной задачи.
В
общее уравнение (27) входят две не заданные
явно функции
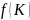 и
и
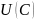 .
Рассмотрим конкретный пример
.
Рассмотрим конкретный пример
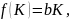
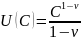 ,
причём пусть
,
причём пусть
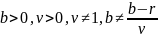 .
Имеем
.
Имеем
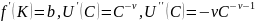 .
Уравнение (27) приобретает вид
.
Уравнение (27) приобретает вид
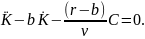
Так
как
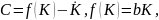 получаем
получаем
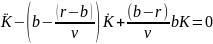 .
(28)
.
(28)
Это
– линейное дифференциальное уравнение
второго порядка с постоянными
коэффициентами, при
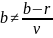 оно имеет общее решение
оно имеет общее решение
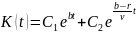 .
(29)
.
(29)
Задача.
Используя
данные
,
получить из уравнения (29) значения
величин
Задача. Найти уравнение Эйлера для задачи отыскания
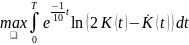
при условиях и решить эту задачу.
ЗАДАЧА С ПОДВИЖНОЙ ГРАНИЦЕЙ. УСЛОВИЯ ТРАНСВЕРСАЛЬНОСТИ
Пусть функция имеет непрерывные частные производные по всем переменным до второго порядка включительно. Поставим часто встречающуюся задачу найти среди функций , имеющих на отрезке непрерывную производную и удовлетворяющих условию
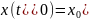
такую, которая является точкой слабого экстремума функционала
При
этом на величину
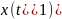 либо не накладывается никаких ограничений
( задача с незакреплённым концом) , либо
требуется, чтобы выполнялось неравенство
либо не накладывается никаких ограничений
( задача с незакреплённым концом) , либо
требуется, чтобы выполнялось неравенство
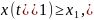 где
где
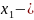 заданная
величина.
заданная
величина.
Уравнение
Эйлера является необходимым условием
и для рассматриваемых задач. Действительно,
если удалось найти решение
какой-то из них и положить
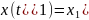 ,
,
то эта функция даёт решение задачи с условиями и, следовательно, для неё выполняется уравнение Эйлера.
Предположим,
что удалось найти общее решение
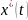 уравнения
Эйлера, зависящее от двух произвольных
постоянных. Условие
даёт одно уравнение. Второе уравнение
получаем из следующих условий
трансверсальности.
уравнения
Эйлера, зависящее от двух произвольных
постоянных. Условие
даёт одно уравнение. Второе уравнение
получаем из следующих условий
трансверсальности.
Для задачи, в которой на величину не накладывается никаких ограничений, это условие имеет вид
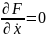 при
при
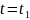 .
(30)
.
(30)
Для
задачи с условием
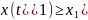 это условие имеет вид
это условие имеет вид
 при
и
при
,
если выполнено неравенство
при
и
при
,
если выполнено неравенство
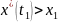 .
.
Примечание.
В
случае задачи с условием
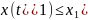 меняем знаки во всех соответствующих
неравенствах.
меняем знаки во всех соответствующих
неравенствах.
Рассмотрим пример.
Задача. В двух случаях найти
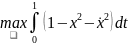 при
условии
при
условии
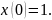
В
первом случае конец
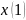 не закреплён. Во втором случае выполнено
неравенство
не закреплён. Во втором случае выполнено
неравенство
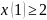 .
.
Уравнение Эйлера принимает вид
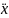 -x=0
-x=0
и его общее решение имеет вид
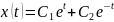 .
.
Условие
 даёт уравнение
даёт уравнение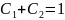 ,
так что общее решение принимает вид
,
так что общее решение принимает вид
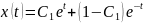 .
(31)
.
(31)
Из (31) находим
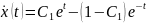 .
(32)
.
(32)
Так
как
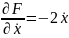 ,
в первом случае условие трансверсальности
даёт
,
в первом случае условие трансверсальности
даёт
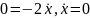 ,
откуда, ввиду (32), находим
,
откуда, ввиду (32), находим
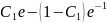 =0,
=0,
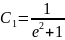
и
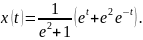
Так
как
)=
 выпуклая
вверх по совокупности переменных
выпуклая
вверх по совокупности переменных
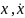 функция,
задача решена.
функция,
задача решена.
Во втором случае из условия получаем
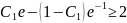
или
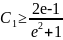 .
(33)
.
(33)
Если
бы выполнялось неравенство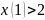 ,
то должно выполняться равенство
,
то должно выполняться равенство
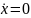 ,
из которого вытекает, что
,
из которого вытекает, что
.
Это
неравенство противоречит неравенству
(33). Следовательно,
 и
и
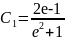 .
.
При
этом
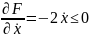 и поэтому единственным возможным
решением является
и поэтому единственным возможным
решением является

Так как )= выпуклая вверх по совокупности переменных функция, и эта задача решена.
Задача. Найти решение задачи с незакреплённым концом:
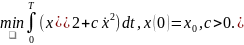
Решение. Уравнение Эйлера для этой задачи:
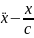 =0.
=0.
Его общее решение имеет вид
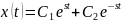 ,
,
где
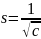 .
Условие
.
Условие
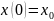 даёт
даёт
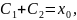 откуда
откуда
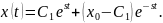
Из
условия трансверсальности
находим
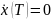 ,
т.е.
,
т.е.
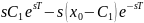 =0,
=0,
откуда
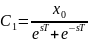
и
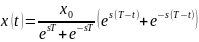
Так
как
)=
 выпуклая
вниз по совокупности переменных
функция,
задача решена.
выпуклая
вниз по совокупности переменных
функция,
задача решена.
Замечание. Рассмотренная задача связана с математической моделью макроэкономической задачи планирования экономики.
Замечание.
Также
следует отметить, что в курсах вариационного
исчисления задача с подвижными границами
обычно рассматривается в более общей
постановке. Требуется, чтобы концы
гладких кривых лежали на двух заданных
линиях
 .
Условия трансверсальности при этом
имеют вид
.
Условия трансверсальности при этом
имеют вид

 .
.
ОБОБЩЕНИЯ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
В вариационном исчислении рассматриваются функционалы, зависящие от производных высших порядков. Пусть
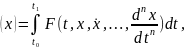 (34)
(34)
где
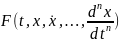 имеет по всем переменным непрерывные
производные до порядка
имеет по всем переменным непрерывные
производные до порядка
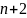 включительно,
включительно,
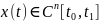 и выполнены условия
и выполнены условия
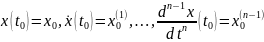 ,
,
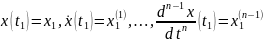 .
.
Экстремалями функционала (34) являются интегральные кривые уравнения Эйлера-Пуассона:
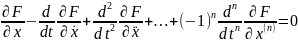 .
.
В вариационном исчислении рассматриваются функционалы, зависящие от нескольких функций одной переменной. Пусть
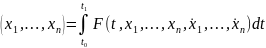 ,
,
где
функция
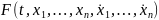 имеет непрерывные производные по всем
аргументам и
имеет непрерывные производные по всем
аргументам и
заданы условия
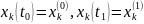 ,
k=1,…,n.
,
k=1,…,n.
Экстремали этого функционала находятся из системы дифференциальных уравнений
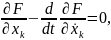 k=1,…,n.
k=1,…,n.
Рассмотрим, наконец, функционалы, зависящие от функций нескольких переменных.
Пусть
 ,
,
где
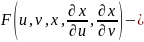 трижды
дифференцируемая функция по совокупности
переменных,
трижды
дифференцируемая функция по совокупности
переменных,
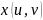 непрерывна вместе со всеми своими
производными до второго порядка
включительно в некоторой области
непрерывна вместе со всеми своими
производными до второго порядка
включительно в некоторой области
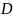 ,
принимающая заданные значения на границе
этой области и дающая экстремум
рассматриваемому функционалу. Тогда
удовлетворяет уравнению Эйлера-Остроградского
( в котором, для краткости, обозначено
,
принимающая заданные значения на границе
этой области и дающая экстремум
рассматриваемому функционалу. Тогда
удовлетворяет уравнению Эйлера-Остроградского
( в котором, для краткости, обозначено
 ):
):
 -
-
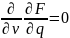 .
.
