
- •Список вопросов по курсу математического анализа, 4 семестр
- •Функционал. Линейное нормированное пространство. Метрическое пространство. Топологическое пространство.
- •Вопрос 8. Определение метрического пространства. Примеры
- •Вопрос 9. Расстояния на множестве непрерывных функций
- •Вопрос 10. Сходимость в метрическом пространстве
- •Вопрос 11. Равномерная сходимость и сходимость в среднем
- •Вопрос 12. Замкнутые множества в метрическом пространстве, их свойства
- •Вопрос 13. Замыкание множества в метрическом пространстве
- •Вопрос 14. Открытые множества в метрическом пространстве
- •Вопрос 15. Полные метрические пространства
- •Вопрос 16.Примеры полных метрических пространств.
- •Вопрос 17. Топологические пространства
- •Вопрос 20. Пространство . Компактные множества в
- •Открытые и закрытые множества в .
- •Сходимость в .
- •Компактные множества в .
- •Вопрос 21. Непрерывные функции и отображения
- •Вопрос 22. Индуцированная топология . Теоремы о максимуме
- •Раздел 12. Элементы вариационного исчисления
Вопрос 13. Замыкание множества в метрическом пространстве
Определение.
Замыкание
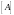 множества
множества
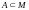 получается присоединением к множеству
получается присоединением к множеству
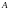 всех его предельных точек.
всех его предельных точек.
Из
определения сразу следует, что
замкнуто тогда и только тогда, когда
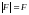 .
.
Лемма
1. Всякая
точка
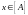 может быть представлена как
,
где
может быть представлена как
,
где
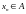 .
.
Либо
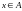 ,
тогда
,
тогда
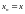 для всех
для всех
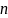 и
доказываемое равенство очевидно. Либо
,
но
и
доказываемое равенство очевидно. Либо
,
но
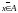 ,
тогда, по определению
,
существует последовательность
:
.
,
тогда, по определению
,
существует последовательность
:
.
Лемма
2.
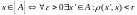 .
.
Необходимость
доказана в лемме 1. Достаточность:
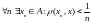 ,
тогда
и
.
,
тогда
и
.
Теорема
. Замыкание
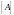 есть наименьшее замкнутое подмножество,
содержащее
есть наименьшее замкнутое подмножество,
содержащее
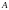 .
.
Требуется
доказать, во-первых, что замыкание
- замкнутое множество и, во-вторых, что
любое замкнутое множество
содержащее
множество
,
 ,
содержит и множество
,
т.е.
,
содержит и множество
,
т.е.
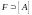 .
.
Пусть
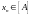 и
.
По лемме 2, для каждого
и
.
По лемме 2, для каждого
 существует точка
существует точка
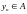 такая , что
такая , что
 .
.
Тогда
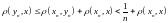 .
Правая часть стремится к
при
.
Поэтому
.
Правая часть стремится к
при
.
Поэтому
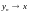 ,
но
,
но
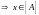 .
.
Далее,
пусть
.
Будучи замкнутым,
содержит пределы всех сходящихся
последовательностей точек из
.
Следовательно,
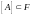 .
.
Вопрос 14. Открытые множества в метрическом пространстве
Определение.
Пусть
- произвольное множество точек из
метрического пространства
.
Точка
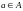 называется внутренней
точкой множества
,
если существует
называется внутренней
точкой множества
,
если существует
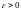 такое, что все точки
с условием
такое, что все точки
с условием
 (т.е.
(т.е.
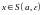 )
также принадлежат
.
)
также принадлежат
.
Множество , все точки которого – внутренние, называется открытым.
Примеры открытых множеств. Интервал на прямой, круг без границы и т.д.
Теорема
.
 открытое
открытое
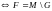 - замкнутое.
- замкнутое.
Пусть
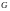 - открытое и пусть
- открытое и пусть
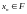 ,
.Если
бы
,
.Если
бы
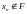 ,
это обозначало бы, что
,
это обозначало бы, что
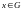 ;
ввиду чего существовала бы
;
ввиду чего существовала бы
 .
Но тогда условие
,
(
.
Но тогда условие
,
(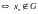 )
невозможно. Т.о.
)
невозможно. Т.о.
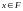 и
- замкнутое, а
.
и
- замкнутое, а
.
Обратно.
Пусть
- замкнутое, а
.
Если бы для любого
существовала точка
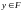 такая, что
такая, что
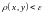 ,
то тогда, по лемме 2 из вопроса 13,
,
то тогда, по лемме 2 из вопроса 13,
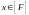 ,
но
- замкнутое,
,
но
- замкнутое,
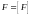 ,
значит
,
что невозможно по условию.
,
значит
,
что невозможно по условию.
Теорема . Объединение любого множества открытых множеств и пересечение конечного числа открытых множеств – открытое множество.
Пусть
 .
Возьмем
,
при некоторых
.
Возьмем
,
при некоторых
 имеем
имеем
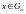 .
Но
.
Но
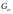 - открытое, и существует
- открытое, и существует
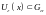 .
Тогда
.
Поэтому
-
открытое.
.
Тогда
.
Поэтому
-
открытое.
Пусть
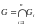 .
Пусть
,
это означает, что
.
Пусть
,
это означает, что
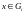 ,
,
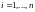 Для каждого
существует
Для каждого
существует
 такое, что
такое, что
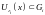 .
.
Выберем
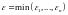 .
Тогда
.
Тогда
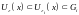 и
и
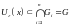 .
.
Используем теоремы и получим
Следствие. Пересечение любого числа замкнутых множеств – замкнутое множество. Объединение конечного числа замкнутых множеств – замкнутое множество.
Пусть
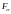 - замкнутое. Обозначим
- замкнутое. Обозначим
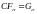 .
Рассмотрим
.
Рассмотрим
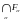 и рассмотрим его дополнение
и рассмотрим его дополнение
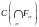 .
.
Напомним законы де Моргана:
 -
открытое множество, по теореме 3. Значит
по теореме 2,
- замкнутое множество.
-
открытое множество, по теореме 3. Значит
по теореме 2,
- замкнутое множество.
Аналогично,
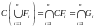 - открытое множество. По доказанной
теореме ,
- открытое множество. По доказанной
теореме ,
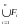 - замкнутое множество.
- замкнутое множество.
Замечание.
Пересечение конечного числа открытых
множеств, по доказанному, открытое
множество, однако пересечение бесконечного
числа открытых множеств может оказаться
замкнутым. Например, пусть
 .
Тогда
.
Тогда
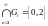 .
Аналогично, объединение бесконечного
числа замкнутых множеств может оказаться
открытым множеством:
.
Аналогично, объединение бесконечного
числа замкнутых множеств может оказаться
открытым множеством:
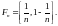 Тогда
Тогда
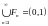 .
.
