Вопрос 11. Равномерная сходимость и сходимость в среднем

3. В пространстве непрерывных функций с расстоянием 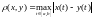сходимость по метрике совпадает с изученным ранее понятием равномерной сходимости последовательности функций.

Действительно, равномерная сходимость 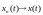означает: 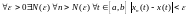. Так как непрерывная на отрезке функция 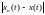достигает на нем своего максимума, условие 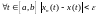совпадает с условием 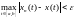, что и означает сходимость по заданной метрике. 

4. Если на пространстве непрерывных функций рассмотреть еще и метрику 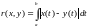, то эта метрика тоже определяет понятие сходимости , так называемую сходимость в среднем.

Можно сравнить понятия равномерной сходимости со сходимостью в среднем. Если последовательность равномерно сходится к предельной функции, то из неравенства приведённого в п.3 условия, т.е. из неравенства

,

следует неравенство ,

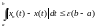означаюшее, что 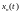сходится к 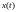в среднем.

Обратное неверно. Действительно, функция 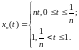стремится в среднем 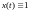к , т.к. 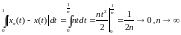. Однако пр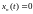и и .

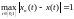Это означает, что требование сходимости в среднем слабее требования равномерной сходимости.

Вопрос 12. Замкнутые множества в метрическом пространстве, их свойства

Определение. Пусть 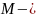метрическое пространство с расстоянием 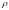. Открытым шаром 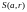(иногда используем обозначения или 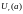) с центро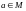м и радиусом 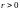называется множество всех точек 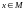с условием 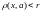. Замкнутый шар 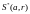состоит из точек .

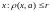Примеры.

1. В 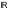открытый шар- интервал 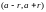, замкнутый шар- отрезок .

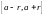2. В 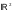открытый шар - круг с центром и радиусом , исключая границу (соответственно, для замкнутого- включая границу).

3. В пространстве 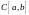непрерывных функций на отрезке 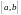с метрикой открытый шар с центром 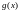представляет собой множество всех функций 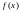таких, что для всех 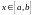выполняется неравенство 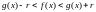. В случае замкнутого шара имеем: .

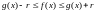Используя понятие шара , отметим, что для того, чтобы выполнялось равенство (в метрическом пространстве 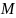) 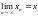, необходимо и достаточно, чтобы .

Определение. Пусть 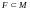. 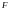- замкнутое подмножество, если для любой сходящейся последовательности , .

Пример. Замкнутый шар- замкнутое множество. Действительно, если .

С понятием замкнутого множества тесно связано понятие предельной точки.

Определение. Пусть 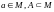. Точка называется предельной точкой множества 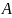, если существует бесконечная последовательность точек 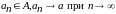, причем такая, что среди этих 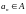бесконечно много различных точек.

Утверждение. Множество замкнутое 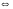оно содержит все свои предельные точки.

 Если множество замкнутое, то оно содержит все предельные точки, так как содержит все точки с условием .

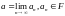В обратную сторону утверждение тоже является верным., так как если существует 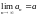и среди значений 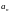лишь конечное множество различных, то, начиная с некоторого 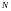_, для всех 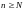имеем 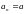, поэтому . 

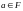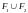Теорема. Если - замкнутые множества, то - замкнутое множество.

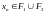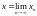Пусть и . Среди 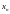существует бесконечное множество 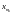таких, что все они принадлежат одному и тому же множеству, 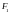или 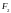(если бы в входило конечное множество , так же и в тоже, то и в входило бы конечное множество членов ). Докажем, .

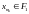Предел подпоследовательности равен пределу последовательности, так что 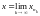и, следовательно, 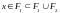, т.е. . 

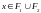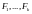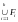Следствие. Если - замкнутые множества, то - замкнутое множество.

Теорема. Пересечение любого множества замкнутых множеств - замкнутое множеств.

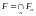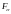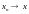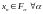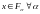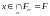Доказательство. Пусть , - замкнуты. Если и , то и, следовательно, , поэтому . Что и требовалось доказать.