Открытые и закрытые множества в .
Открытый
шар
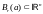представляет собой множество точек
,
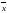удовлетворяющих
условию
.
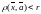Это множество также называют окрестностью
точки радиуса .
Есл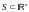и
и
,
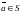и если существует такое r, что
,
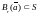то такая точка
называется внутренней точкой S. Множество - открытое, если любая его
точка - внутренняя.
Напомним свойства открытых множеств:
-
открытые множества.
Объединение
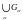любого
множества открытых множеств – открытое
множество.Пересечение конечного множества открытых множеств – открытое множество.
(Разумеется, пересечение бесконечного множества открытых множеств
не
обязательно открытое множество: в
,
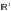например, пересечение
интервалов
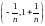есть отрезок
).
Дополнением
к
множеству
называется множество
.
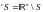Точка называется граничной точкой множества S, если любая ее окрестность
содержит
как точки из S, так и точки из
.
Сама граничная точка множества S, разумеется, является граничной
точкой и для и принадлежит одному из этих множеств.
Множество,
состоящее из граничных точек S, называется
границей
S и обозначается
.
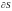Например,
.
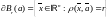Множество S называется замкнутым, если оно содержит все свои граничные точки.
Была доказана теорема.
Теорема.Дополнение к открытому множеству- замкнутое множество,
дополнение к замкнутому- открытое.
Замкнутые множества обладают следующими свойствами:
- замкнутые множества.
Пересечение
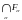любого множества замкнутых множеств
–
замкнутое множество.
Объединение конечного числа замкнутых множеств – замкнутое множество.
(Объединение бесконечного множества замкнутых множеств не обязательно
замкнутое
множество. Пример:
).
Разумеется, множество может быть ни открытым, ни замкнутым;
например,
полуинтервал
.
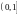Еще раз отметим: любая граничная точка множества S принадлежит либо S, либо .
Если все граничные точки принадлежат , то S – открытое множество. Если все
они принадлежат S, то S – замкнутое множество. Если часть граничных точек
множества S принадлежит S, а другая часть, тоже непустая, принадлежит , то S
не является ни открытым, ни замкнутым.
Сходимость в .
Последовательностью в называется отображение, сопоставляющее каждому
номеру
k элемент
.
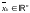Последовательность
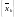называется сходящейся
к
элементу
,
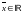если
.
Это
обозначается так:
,
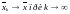либо
.
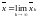Пусть
.
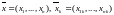Сходимость
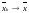означает, что
.
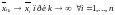(Это равносильные записи).
Последовательность называется фундаментальной (или последовательностью Коши),
если
.
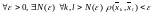Имеет место следующий критерий Коши сходимости последовательности:
последовательность
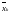сходится к некоторому элементу
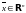тогда и только
тогда, когда она фундаментальная.
Ограниченные множества в
.
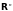Определение.
Множество
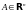- ограниченное,
если существует шар
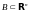такой, что
.
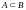Множество, не являющееся ограниченным, называется неограниченным.
По аналогии с этим определением, назовем последовательность ограниченной,
если множество принимаемых ею значений- ограниченное множество в .
В противном случае она называется неограниченной. Можно доказать, что S
ограничено
тогда и только тогда, когда любая
последовательность элементов
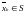
содержит
подпоследовательность элементов
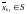такую, что
,
.