
- •Список вопросов по курсу математического анализа, 4 семестр
- •Функционал. Линейное нормированное пространство. Метрическое пространство. Топологическое пространство.
- •Вопрос 8. Определение метрического пространства. Примеры
- •Вопрос 9. Расстояния на множестве непрерывных функций
- •Вопрос 10. Сходимость в метрическом пространстве
- •Вопрос 11. Равномерная сходимость и сходимость в среднем
- •Вопрос 12. Замкнутые множества в метрическом пространстве, их свойства
- •Вопрос 13. Замыкание множества в метрическом пространстве
- •Вопрос 14. Открытые множества в метрическом пространстве
- •Вопрос 15. Полные метрические пространства
- •Вопрос 16.Примеры полных метрических пространств.
- •Вопрос 17. Топологические пространства
- •Вопрос 20. Пространство . Компактные множества в
- •Открытые и закрытые множества в .
- •Сходимость в .
- •Компактные множества в .
- •Вопрос 21. Непрерывные функции и отображения
- •Вопрос 22. Индуцированная топология . Теоремы о максимуме
- •Раздел 12. Элементы вариационного исчисления
Список вопросов по курсу математического анализа, 4 семестр
Определение метрического пространства. Примеры.
Расстояния на множестве непрерывных функций.
Сходимость в метрическом пространстве .
Равномерная сходимость и сходимость в среднем.
Замкнутые множества в метрическом пространстве, их свойства.
Замыкание множества в метрическом пространстве.
Открытые множества в метрическом пространстве.
Полные метрические пространства.
Примеры полных метрических пространств.
Топологические пространства.
Счетные множества.
Несчётные множества.
Пространство
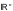 . Компактные множества в
.
. Компактные множества в
.Непрерывные функции
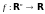 и отображения
и отображения
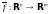 .
.Индуцированная топология . Теоремы о максимуме.
Функционал. Линейное нормированное пространство. Метрическое пространство. Топологическое пространство.
Пространства
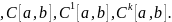 Непрерывность функционала.
Непрерывность функционала.Функционал. Линейное нормированное пространство. Метрическое пространство. Топологическое пространство.
Пространства
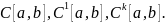 Непрерывность функционала.
Непрерывность функционала.Вариация функционала.
Уравнение Эйлера.
Уравнение Эйлера для математической модели задачи Рамсея.
Лектор д.ф.-м.н. В.Г.Чирский
Вопрос 8. Определение метрического пространства. Примеры
Выше мы разбирали конкретные примеры множеств, в которых было определено расстояние между их элементами. При этом эти множества имели различную природу: точки на плоскости и в пространстве, наборы чисел, как конечные, так и бесконечные, непрерывные на отрезке функции и т.д. Дадим общее определение метрического пространства.
Определение.
Метрическим
пространством
называется
множество М, в котором для любых его
элементов x, y определено число
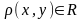 ,
,
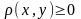 ,
называемое расстоянием
между
x и y, обладающее такими свойствами:
,
называемое расстоянием
между
x и y, обладающее такими свойствами:
1.)
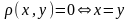 ;
;
2.)
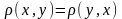 (симметрия) для любых x, y Î
M;
(симметрия) для любых x, y Î
M;
3.)
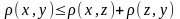 (аксиома треугольника) для любых x, y, z Î
M.
(аксиома треугольника) для любых x, y, z Î
M.
Часто элементы метрического пространства М называют его точками.
Рассмотрим некоторые примеры.
Пространство
 состоит
из точек
состоит
из точек
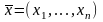 и расстояние в нём определено формулой
и расстояние в нём определено формулой
 .
.
То,
что эта функция обладает свойствами
расстояния, проверялось неоднократно.
Первые 2 свойства очевидны, третье имеет
вид
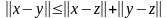 или
или
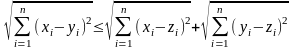 которое следует из неравенства
которое следует из неравенства
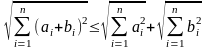 при подстановке
при подстановке
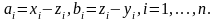
Это неравенство, в свою очередь, следует из неравенства
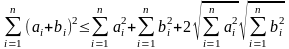 ,
равносильного неравенству
,
равносильного неравенству
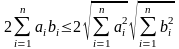 ,
следующему из неравенства
,
следующему из неравенства
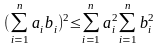
Последнее
неравенство выполняется потому, что
оно означает, что дискриминант квадратного
трехчлена
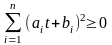 не положителен.
не положителен.
Пространство
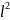 бесконечных последовательностей
бесконечных последовательностей
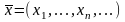 с условием
с условием
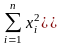 .
.
В
нём расстояние определено формулой
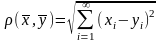 .
.
Условия
1 и 2 снова очевидны, а условие
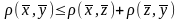 следует из неравенства
следует из неравенства
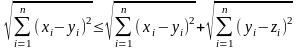 при
предельном переходе n®¥.
при
предельном переходе n®¥.
То,
что существует предел, например,
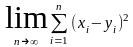 следует
из существования, по условию, пределов
следует
из существования, по условию, пределов
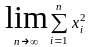 ,
,
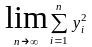 и неравенства
и неравенства
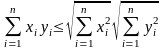 .
.
На множестве наборов чисел (x1,…, xn) можно ввести и другое расстояние
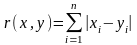 .
.
Действительно,
свойства 1 и 2 снова очевидны. Свойство
3 следует из неравенства
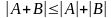 ,
так как
,
так как
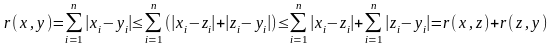
4.
Точно так же, рассмотрим множество
последовательностей (векторов с
бесконечным числом координат)
с условием
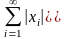 .
.
Положим
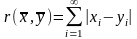 .
.
Первые 2 условия расстояния очевидны, третье получается из неравенства примера 3 предельным переходом при n®¥.
