
- •Список вопросов по курсу математического анализа, 4 семестр
- •Функционал. Линейное нормированное пространство. Метрическое пространство. Топологическое пространство.
- •Вопрос 8. Определение метрического пространства. Примеры
- •Вопрос 9. Расстояния на множестве непрерывных функций
- •Вопрос 10. Сходимость в метрическом пространстве
- •Вопрос 11. Равномерная сходимость и сходимость в среднем
- •Вопрос 12. Замкнутые множества в метрическом пространстве, их свойства
- •Вопрос 13. Замыкание множества в метрическом пространстве
- •Вопрос 14. Открытые множества в метрическом пространстве
- •Вопрос 15. Полные метрические пространства
- •Вопрос 16.Примеры полных метрических пространств.
- •Вопрос 17. Топологические пространства
- •Вопрос 20. Пространство . Компактные множества в
- •Открытые и закрытые множества в .
- •Сходимость в .
- •Компактные множества в .
- •Вопрос 21. Непрерывные функции и отображения
- •Вопрос 22. Индуцированная топология . Теоремы о максимуме
- •Раздел 12. Элементы вариационного исчисления
Вопрос 9. Расстояния на множестве непрерывных функций
Рассмотрим множество непрерывных на отрезке [a,b] функций.
Нашей целью является введение расстояния на этом множестве несколькими различными способами.
Определим
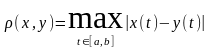 .
.
(то, что максимум достигается, следует из теоремы Вейерштрасса из первого семестра: непрерывная на отрезке функция достигает минимального и максимального значений).
Снова очевидны первые 2 свойства расстояния. Неравенство
треугольника проверяется так:
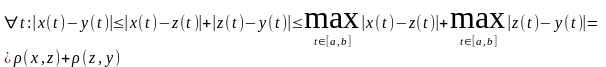
Еще пример: множество непрерывных на отрезке функций с расстоянием
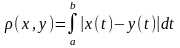 .
.
В
этом случае очевидным является свойство
2. Третье свойство получается интегрированием
неравенства
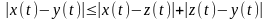 .
.
Докажем свойство 1, т.е. докажем, что если
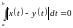 ,
,
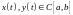 ,
то
,
то
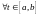
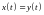 .
.
Для
этого достаточно доказать, что если
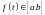 и
и
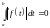 ,
то
,
то
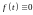 .
.
Предполагая
противное, получим, что существует точка
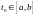 :
:
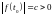 .
Тогда, по непрерывности,
.
Тогда, по непрерывности,
 :
:
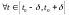
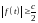 и тогда
и тогда
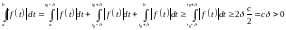 ,
вопреки условию.
,
вопреки условию.
Рассмотренные выше примеры показывают, что на одном и том же множестве можно ввести разные функции расстояния, получая при этом, разумеется, различные метрические пространства.
Введём расстояние по формуле
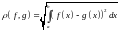 (с таким
(с таким
расстоянием мы имели дело при изучении рядов Фурье).
Свойство 2) расстояния очевидно, свойство 1) расстояния в примере 3 проверяется точно так же, как в примере 2.
Свойство
3) расстояния проверяется так: рассмотрим
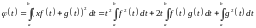 ,
т.к.
,
т.к.
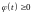 для
для
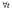 (интеграл от неотрицательной функции
неотрицателен). Поэтому дискриминант
этого квадратного трехчлена неположителен,
откуда
(интеграл от неотрицательной функции
неотрицателен). Поэтому дискриминант
этого квадратного трехчлена неположителен,
откуда
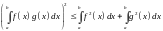
Это так называемое неравенство Буняковского. Из этого неравенства получаем
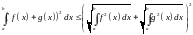 и
и
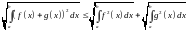 это интегральная
форма неравенства треугольника.
это интегральная
форма неравенства треугольника.
Положив
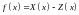 и
и
 ,
получим
,
получим
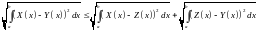 ,
ч.т.д.
,
ч.т.д.
Можно было бы ввести и другие расстояния, используя неравенство Минковского
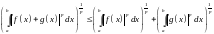
для доказательства «неравенства треугольника» , т.е. свойства 3 расстояния. Все остальные свойства расстояния проверялись бы аналогично тому, как это сделано в предыдущем примере.
В предыдущем и следующих примерах мы ограничимся рассмотрением множества непрерывных функций. Однако введённое в примере 3 расстояние более естественно рассматривать не только на множестве непрерывных функций, а на более широком множестве; для этого используется понятие интеграла Лебега. Рекомендуем заинтересовавшимся этим вопросами обратиться, например, к классической книге: А.Н. Колмогоров, С.В. Фомин «Элементы теории функций и функционального анализа».
Вопрос 10. Сходимость в метрическом пространстве
Определение.
Точка
 метрического
пространства
метрического
пространства
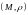 (т.е. множества
(т.е. множества
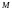 с
функцией расстояния
с
функцией расстояния
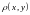 )
называется пределом
бесконечной последовательности точек
)
называется пределом
бесконечной последовательности точек
 ,
если
,
если
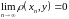 (это обозначается, как обычно:
(это обозначается, как обычно:
 или
или
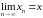 ).
).
Иными
словами, говорят, что
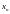 сходится
к
по метрике
пространства (или
по расстоянию).
сходится
к
по метрике
пространства (или
по расстоянию).
Разумеется,
предел, если существует, то только один:
если
и
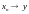 ,
то
,
то
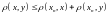 ,
откуда при
,
откуда при
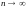 получаем, что
получаем, что
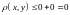 ,
,
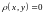 и
и
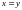 .
.
В пространстве
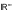 сходимость
сходимость
 ,
по метрике равносильна тому, что для
любого
,
по метрике равносильна тому, что для
любого
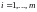 ,
,
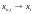 ,
,
т.е покоординатной
сходимости.
,
,
т.е покоординатной
сходимости.
Действительно,
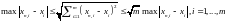 ,
поэтому если
,
то
,
поэтому если
,
то
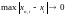 ,
т.е. при любом
,
т.е. при любом
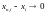 при
.
Обратно, если для всех
при
,
то
при
,
следовательно
при
.
Обратно, если для всех
при
,
то
при
,
следовательно
 при
.
при
.
Однако в пространстве
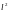 (см.пример
2 вопроса 8) из сходимости по метрике
вытекает покоординатная сходимость,
но не наоборот.
(см.пример
2 вопроса 8) из сходимости по метрике
вытекает покоординатная сходимость,
но не наоборот.
Действительно,
если
,
то
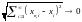 при
,
поэтому для любого
при
,
поэтому для любого
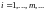 получаем
получаем
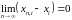 ,
т.е.
при
,
т.е.
при
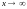 .
.
Обратно,
возьмём в качестве
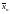 вектор
вектор
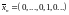 ,
все координаты которого, кроме
,
равны 0, и
,
все координаты которого, кроме
,
равны 0, и
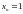 .
.
Для
любого фиксированного
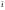 последовательность
последовательность
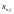 имеет вид:
имеет вид:
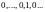 (все члены последовательности, кроме
-го
равен 0,
(все члены последовательности, кроме
-го
равен 0,
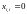 .
Однако вектор
.
Однако вектор
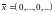 не является пределом последовательности
,
так как для
не является пределом последовательности
,
так как для
любого
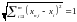 ,
а не стремится к
,
а не стремится к
 при
.
при
.
