Компактные множества в .
Множество
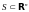называется компактным,
если оно ограниченное и замкнутое в
.
Это - одно из возможных определений компактности, не самое общее.
Часто используется такое определение: множество S в метрическом пространстве M
называется
компактным,
если из любого покрытия S открытыми
множествами
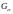
(т.е.,
)
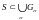можно выделить конечное подпокрытие
,
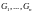т.е.
.
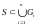В эти условия равносильны.
Можно также указать следующую характеристику компактных множеств:
S компактно тогда и только тогда, когда любая последовательность , ,
содержит
подпоследовательность
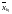такую, что
и
.
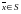Вопрос 21. Непрерывные функции и отображения
Определение.
Функция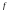
-,
определенная в области
,
называется непрерывной
в
точке
,
если
.
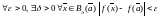Функция представляет собой частный случай отображения .
Отображение
задается совокупностью функций
:
.
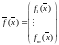Непрерывность
отображения
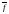в точке
задается условием:
,
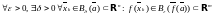- и равносильна непрерывности
каждой
из функций
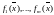в точке
.
Важный
частный случай отображения – вектор-
функция
,
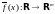задаваемая
функциями :
.
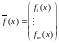Данное выше определение непрерывности – определение Коши. Другое, равносильное
определение непрерывности функции, это определение по Гейне-Борелю.
-
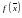непрерывная в точке
функция, если для любой последовательности
,
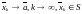значения
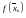стремятся к
.
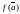Можно доказать (это уже было сделано ранее) равносильность этих определений.
Разумеется, это определение дословно переносится на отображения
(стоит только заменить на ).
Важное свойство непрерывного отображения утверждает следующее: если -
компактное
множество в
,
а
- непрерывное отображение, то
-
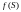компактное
множество в
.
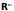Эти теоремы – прямое обобщение теоремы о свойствах непрерывных на отрезке
функций, которые, объединив, можно сформулировать так:
Если функция непрерывна на отрезке, то ее значения на этом отрезке сами
образуют отрезок, соединяющий ее наименьшее и наибольшее значения.
Сформулируем важный критерий непрерывности отображения .
непрерывно
тогда и только тогда, когда для любого
открытого множества
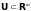
его
полный прообраз
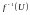- открытое подмножество
.
Равносильное утверждение:
непрерывно тогда и только тогда, когда для любого замкнутого
множества
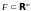его полный прообраз
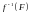- замкнутое множество в
.
Пример.
Пусть,
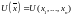- функция
полезности.
Если
,
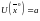то множество
называем
множеством верхнего
уровня.
(upper level set) или
множеством верхнего контура (upper contour set).
Пусть
.
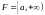Тогда
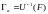и если
- непрерывная функция,
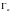- замкнутое
подмножество.
Множества
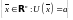называют поверхностями
безразличия
(indifference surfaces).
Вопрос 22. Индуцированная топология . Теоремы о максимуме
Индуцированная топология
В ряде задач задано множество и рассматриваются только его подмножества.
Например,
для функции Кобба-Дугласа
.
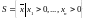На этом множестве определена индуцированная топология
(иногда
ее называют относительной), в которой
шар
.
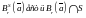Можно говорить о граничных точках, внутренних точках, открытых и замкнутых
множествах в индуцированной топологии.
В
качестве примера отметим критерий
непрерывности отображения
,
.
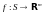непрерывно тогда и только тогда, когда полный прообраз для любого
открытого
множества
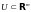является открытым множеством с
индуцированной топологией. (Аналогичное утверждение верно и
для замкнутых множеств).
Теоремы о максимуме
В экономической теории известны результаты сравнительной статики
(comparative statics). Они описывают поведение оптимального решения
задачи в зависимости от изменения параметров, например, цен. Возникает вопрос
о существовании оптимального решения. Ответ на него таков.
Пусть
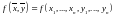- непрерывная функция на
,
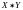где
.
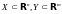Пусть
-
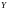компакт. Тогда для любого фиксированного
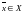функция
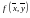
непрерывна на компакте и, следовательно, достигает на нем наименьшего и
наибольшего значений.
Это наибольшее значение зависит от . Определим функцию
оптимального
значения
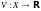формулой
.
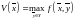Эта
функция
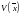- непрерывная функция от
.
Поэтому к ней применим
сделанный выше вывод о достижении ею на компакте максимального значения.