1.5.14.8.2. Разложение по формуле Маклорена некоторых элементарных функций

1) f(x)=e^x, f⁽ⁿ⁾(x)= e^x, f⁽ⁿ⁾(0)=1 nN,

.

Остаточный член в форме Лагранжа равен

.

На любом сегменте [-r, r] (r>0) в силу того, что ,

получим следующую оценку остаточного члена:

.

2) f(x)=sinx. Поскольку (доказывается методом математической индукции),

(1)

Формула Маклорена имеет вид:

.

Мы записали R_2n+3(x), а не R_2n+2(x), т.к. все члены разложения с четными номерами в силу (1) равны нулю.

.

На любом сегменте [-r, r] (r>0) .

3) f(x)=cosx. Поскольку ,

(2)

Формула Маклорена имеет вид:

.

Мы записали R_2n+2(x), а не R_2n+1(x), т.к. следующий за последним выписанным слагаемым член многочлена Тейлора в силу (2) равен нулю.

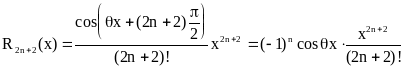
На любом сегменте [-r, r] .

4) f(x)=ln(1+x)

Формула Маклорена имеет вид:

.

Остаточный член запишем в формах Лагранжа и Коши

(в форме Лагранжа). (3)

(в форме Коши). (4)

Пусть x(0, 1], тогда

(следует из (3)),

т.к. x>0,

.

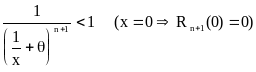Оценим теперь на [-r, 0], где 0<r<1.

Будем исходить из формы Коши для R_n+1(x).

Перепишем этот остаточный член в виде

.

Заметим, что для x[-r, 0], 0<r<1

1-<1+x  x>-  x+>0  (x+1)>0  x>-1

(что верно по предположению)

.

Таким образом, R_n+1(x)0 при n x[-r, 1], где r<1.

5) f(x)=(1+x)^, где  - вещественное число

Формула Маклорена имеет вид:

,

где остаточный член в форме Лагранжа равен

.

В частном случае, когда =n - целое число, R_n+1(x)=0 и мы получим формулу бинома Ньютона

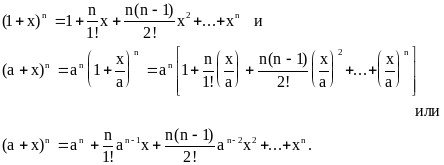
Итак, общий случай бинома Ньютона является частным случаем формулы Маклорена.

1.5.14.8.3. Приложения формулы Маклорена Приближенное вычисление числа е

. Ранее были установлены оценки 2 е<3. Положим в формуле Маклорена для e^x, х=1 и r=1, получим

,

где

.

Выбирая номер n достаточно большим, получим приближенное значение e с любой наперед заданной точностью.

1.5.14.8.4. Вычисление пределов с помощью формулы Маклорена

Из полученных нами ранее разложений по формуле Маклорена элементарных функций легко следуют более грубые разложения (с остаточным членом в форме Пеано).

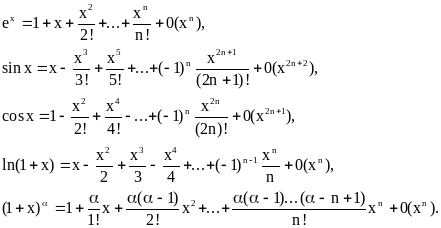
Эти разложения могут быть использованы при вычислении пределов функций при x0.

Пример. Вычислить .

Так как в знаменателе старшая степень x - третья, то в числителе нужно учитывать степени, не выше третьей.

Получим разложения функций, входящих в числитель, до членов с x³.

. (1)

Так как , 0[(sinx)³]=0(x³),

далее,

.

Подставляя это разложение в (1) будем иметь

.

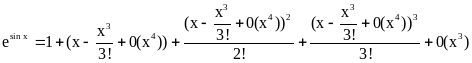Раскрывая скобки и учитывая, что x^k0(x^m)=0(x^m+k)=0(x^m), получим

Получим теперь разложение tgx

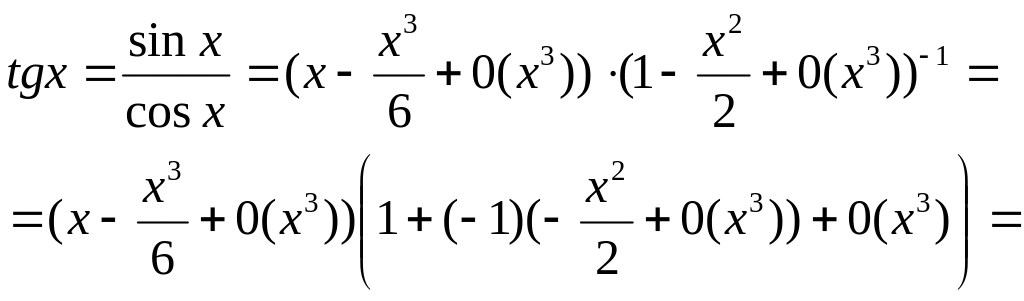
Здесь использовано разложение (1+z)^-1=1-z+о(z)

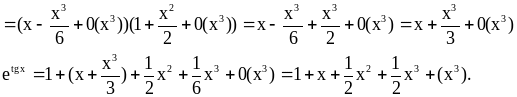
Подставляя в заданную функцию полученные разложения, будем иметь

В этом примере использование правила Лопиталя было бы затруднительным, в то время как применение формулы Маклорена опиралось только на известные разложения элементарных функций.

1 См., например: Ильин В.А., Позняк Э.Г. Основы математического анализа.-

-М.: Наука, 1971 (и последующие издания), ч.1.

* Функция y=Ax+B, где A -линейная функция аргумента x, где A и B- некоторые

постоянные. Если В=0, то линейная функция называется однородной.

1 Доказательство см.: Ильин В.А., Позняк Э.Г. Основы математического анализа. -М.:

Наука, 1971 (и последующие издания) ч.1.

150