1.7. Определенный интеграл и его геометрические приложения Для замечаний

1.7. Определенный интеграл и его геометрические приложения

1.7.1. Интегрируемость функции на сегменте.

Рис.1

Пусть функция f(x) задана на сег­менте [a,b] (a<b). Обозначим че- рез Т разбиение [a,b] при помощи не совпадающих друг с другом то- чек a=x0<x1<...<xn=b на n частич- ных сегментов [x0,x1]...[xn-1, xn]. Точки x0,x1,...,xn называются точ- ками разбиения Т. Пусть - произвольная точка частичного сегмента [xi-1,xi]. Разность xi=xi -xi-1 будем называть длиной частич- ного сегмента [xi-1,xi].

Определение 1. Число , где

называется интегральной суммой функции f(x), соответствующей данному разбиению Т сегмента [a,b] и данному выбору промежуточных точек на частичных сегментах [x_i-1,x_i].

Обозначим - диаметр разбиения Т сегмента [a,b].

Геометрический смысл интегральной суммы . Рассмотрим криволинейную трапецию - фигуру, ограниченную графиком функции f(x) (будем считать ее положительной и непрерывной), двумя ординатами, проведенными в точках a и b оси абсцисс и осью абсцисс.

Интегральная сумма - площадь ступенчатой фигуры (рис.1).

Определение 2. Число I называется пределом интегральных сумм при 0, если для >0 можно указать такое положительное число , что для любого разбиения Т сегмента [a,b], максимальная длина  частичных сегментов которого <, независимо от выбора точек на сегментах [x_i-1,x_i] выполнено неравенство

Если интегральная сумма при 0 имеет пределом число I, то будем записывать это так .

Определение 3. Функция f(x) называется интегрируемой по Риману на [a,b], если существует конечный предел I интегральных сумм этой функции при 0. Указанный предел I называется определенным интегралом функции f(x) по [a,b] и обозначается так:

Из рисунка видно, что определенный интеграл численно равен площади криволинейной трапеции, определяемой графиком функции f(x) на [a,b].

Справедлива следующая теорема. Неограниченная на [a,b] функция f(x) не интегрируема на этом сегменте.

Доказательство: Пусть функция f(x) неограничена на [a,b], тогда она неограничена на некотором частичном сегменте [x_k-1,x_k] любого данного разбиения Т сегмента [a,b]. Тогда слагаемое f( )x_k интегральной суммы , отвечающее этому разбиению Т, за счет выбора т. может быть сделано как угодно большим по абсолютной величине, т.е. интегральные суммы , отвечающие любому разбиению Т, не ограничены, и поэтому не существует конечного предела интегральных сумм. Итак, будем рассматривать лишь ограниченные на [a,b] функции.

Замечание: Отметим, что вообще говоря, не всякая ограниченная на [a,b] функция является интегрируемой на этом сегменте.

Проверьте это положение для функции Дирихле (значения в рациональных точках 1, а в иррациональных - 0). Эта функция не интегрируема на [a,b].

1.7.2. Верхние и нижние суммы Дарбу и их свойства.

Пусть функция f(x) - ограниченная на [a,b] функция, т.е. (m,M) (x[a,b]):[m  f(x)  M]. Т - разбиение [a,b] точками a=x₀<x₁<...<x_n=b.

Обозначим через M_i - точную верхнюю и через m_i - точную нижнюю грани этой функции на [x_i-1,x_i].

Суммы

называются верхней и нижней суммами функции f(x) для данного разбиения Т сегмента [a,b].

Заметим, что любая интегральная сумма данного разбиения Т сегмента [a,b] заключена между верхней и нижней суммами S и s этого разбиения.

Геометрический смысл верхней и нижней сумм. Рассмотрим для простоты положительную и непрерывную функцию f(x) и криволинейную трапецию, определяемую этой функцией.

Рис.1 Рис.2

M_i и m_i в случае непрерывности функции представляют собой максимальное и минимальное значения этой функции на частичном сегменте [x_i-1,x_i] разбиения Т, S и s - площади заштрихованных ступенчатых фигур, изображенных на рисунках 1 и 2 соответственно.

Свойства верхних и нижних сумм подробно изложены в [2] (стр. 321-323), поэтому приведем лишь формулировки теорем и прокомментируем каждую из них с помощью рисунков.

Свойство 1. Для любого фиксированного разбиения Т и для любого >0 промежуточные точки на сегментах [x_i-1,x_i] можно выбрать так, что интегральная сумма будет удовлетворять неравенствам 0S- <. Точки можно выбрать и таким образом, что интегральная сумма будет удовлетворять неравенствам 0 -s<.

Рис. 3

На рисунке 3 изображен графикфункции f(x), заданной на сегменте [a,b]. - промежуточные точки на частичных сегментах [xi-1,xi] Преобразуем разность S- = M1x1 + M2x2 +... Mixi +...+ Mnxn -- f( )x1- f( )x2-...- -f( )xi -...- f( )xn = = [M1-f( )]x1+[M2-f( )]x2+...+ +[Mi- f( )]xi+...+[Mn- f( )]xn.

Здесь S - верхняя сумма. Каждое слагаемое последней суммы представляет собой площадь заштрихованного прямоугольника, поэтому S- есть сумма площадей заштрихованных прямоугольников, которая, очевидно, может быть сколь угодно уменьшена за счет выбора точек (если промежуточные точки выбирать близкими к точкам сегментов [x_i-1,x_i], в которых функция f(x) принимает значения M_i).

Для нижних сумм рассуждения проводятся аналогичным образом.

Свойство 2. Если разбиение сегмента [a,b] получено путем добавления новых точек к точкам разбиения Т этого сегмента, то верхняя сумма разбиения не больше ( S) верхней суммы S разбиения Т, а нижняя сумма разбиения не меньше (s ) нижней суммы s разбиения Т.

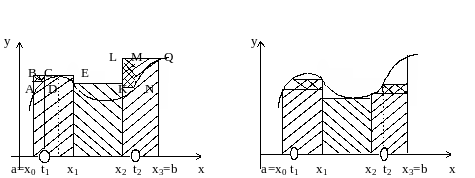
Рис. 4 Рис. 5

На рис. 4 точки x₀, x₁, x₂, x₃ - точки разбиения сегмента [a,b], соответствующие разбиению Т. Кружками отмечены новые точки t₁, t₂, которые вместе с точками x_i дают новое разбиение сегмента [a,b].

Сегменты [x₀,x₁] и [x₂,x₃] поделились на сегменты [x₀,t₁], [t₁,x₁] и [x₂,t₂], [t₂,x₃], соответственно. Верхняя сумма на сегментах [x₀,t₁] и [x₂,t₂] уменьшилась на величину, равную площадям прямоугольников ABCD и KLMN, а на остальных частичных сегментах осталась без изменения, поэтому верхняя сумма разбиения уменьшилась по сравнению с верхней суммой S.

На рис.5 приведена аналогичная картина для нижних сумм.

Свойство 3. Пусть и любые два разбиения [a,b]. Тогда нижняя сумма одного из этих разбиений не превосходит верхнюю сумму другого. Именно, если , ; , соответственно нижние и верхние суммы разбиений и , то  ; < .

Рис.6

На рис. 6 одинарной штриховкой показана верхняя сумма разбиения сегмента [a,b] точками x0=a<x1<x2<x3=b, а двойной штриховкой - нижняя сумма разбиения сегмента [a,b] точками 0=a<1<2<3<4=b

Свойство 4. Множество верхних сумм данной функции f(x) для всевозможных разбиений сегмента [a,b] ограничено снизу. Множество нижних сумм ограничено сверху.

Обозначим через точную нижнюю грань множества верхних сумм , а через точную верхнюю грань множества нижних сумм . Числа и называются соответственно нижним и верхним интегралами Дарбу от функции f(x). Легко показать, что 

Свойство 5. Пусть разбиение [a,b] получено из разбиения Т добавлением к последнему р новых точек, и пусть , ; s, S - соответственно нижние и верхние суммы разбиений и Т. Тогда для разностей S- и -s может быть получена оценка, зависящая от максимальной длины  частичных сегментов разбиения Т, числа р добавленных точек и точных верхней и нижней граней М и m функции f(x) на сегменте [a,b], а именно: S- (M-m)р и -s (M-m)р

Рис.7

На рис.7 точки x₀ = a < x₁ < x₂ < x₃ < x₄ = b соответствуют разбиению Т сегмента [a,b], а две добавленные точки ₁ и ₂ образуют вместе с точками x_i: x₀=a<₁<x₁<x₂<₂<x₃<x₄=b разбиение этого сегмента.

Одинарной штриховкой показана верхняя сумма S разбиения Т, а двойной штриховкой два прямоугольника, сумма площадей которых дает уменьшение S до величины . Если через М и m обозначить точные верхнюю и нижнюю грани функции f(x) на [a,b], а через  максимальную длину частичного сегмента [x_i-1,x_i] разбиения Т, то площадь прямоугольника ABCD, равная (M-m)x будет больше площади каждого из двух прямоугольников, заштрихованных двойной штриховкой, отсюда очевидна оценка: S- (M-m)2 (здесь 2 - число добавленных точек). Для нижних сумм может быть дана аналогичная интерпретация.

В заключение данной темы приведем без доказательства формулировку теоремы, известной под названием леммы Дарбу, имеющей фундаментальное значение для построения теории в теме “Определенный интеграл”.

Лемма Дарбу. Верхний и нижний интегралы Дарбу и от функции f(x) по сегменту [a,b] являются соответственно пределами верхних и нижних сумм при 0, т.е. и .

Замечание 1. Число , например, называется пределом верхних сумм S при 0, если .

Замечание 2. В случае, когда = = I лемма Дарбу позволяет переходить к пределам в неравенствах вида при стремлении к нулю диаметра  разбиения Т сегмента [a,b]. При этом sI и SI, откуда .