1.5. Дифференциальное исчисление Для замечаний

1.5.15. Исследование поведения функций с помощью производных.

1.5.15.1. Условие постоянства функций.

Теорема 1.

Пусть функция f(x) определена, дифференцируема на интервале Х, и на Х. Тогда функция f(x) является постоянной на Х.

Доказательство. Пусть x₀ - некоторая фиксированная точка из Х и х-любая другая точка из Х. Для сегмента [x₀, x] (или [x, x₀]) удовлетворены все условия теоремы Лагранжа, следовательно, между точками х₀ и х найдется точка , такая что Так как f’()=0, то для , т.е. значение функции f(x) в любой точке хХ равно ее значению в фиксированной точке х₀, т.е. постоянна всюду в Х.

Замечание. Геометрический смысл теоремы: если касательная в каждой точке некоторого участка графика функции y=f(x) параллельна оси ОХ, то этот участок есть отрезок прямой, параллельный оси ОХ.

1.5.15.2. Признак монотонности функции

Теорема. (Достаточное условие возрастания (убывания) функции на интервале Х).

Пусть функция f(x)

1) определена на интервале Х;

2) имеет на Х конечную производную ;

3) >0 ( <0) на Х.

Тогда f(x) является возрастающей (убывающей) на интервале Х.

Доказательство. Рассмотрим случай, когда <0 на Х. Возьмем любые два значения х₁ и х₂ из Х такие, что х₁ < х₂, тогда на сегменте [х₁, х₂] f(x) удовлетворяет всем условиям теоремы Лагранжа, поэтому справедливо равенство где - некоторая точка из (х₁, х₂): х₁<< х₂. Так как х₂> х₁, и , что означает убывание функции на множестве Х.

Для случаев >0 на Х доказательство проводится аналогично.

Замечание 1. Положительность (отрицательность) производной на Х не является необходимым условием возрастания (убывания) функции f(x), т.е. если на некотором участке функция возрастает (убывает), то отсюда не следует, вообще говоря, что на этом участке производная этой функции всюду положительна (отрицательна).

Рис.1

Например, для возрастающей на всей числовой оси функции производная в точке х=0 обращается в (рис.1).

Замечание. Геометрическая интерпретация теоремы: поскольку производная функции представляет собой угловой коэффициент касательной к графику функции, то знак производной показывает, острый (если >0) или тупой (если <0) угол с положительным направлением оси ОХ составляет касательная к f(x). В соответствии с этим, кривая идет вверх (функция f(x) возрастает) или вниз (функция f(x) убывает). В отдельных точках при этом касательная может быть параллельной оси ОХ, что соответствует обращению в нуль производной функции f(x) (рис.2,3)

.

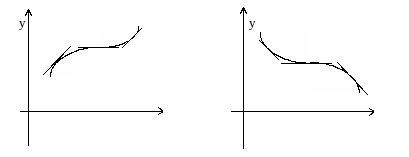Рис.2 Рис.3

1.5.15.3. Экстремум дифференцируемой функции

Необходимое условие экстремума функции в точке : если f(x) дифференцируема в точке С и имеет в этой точке локальный экстремум, то Таким образом, экстремум дифференцируемой функции следует искать лишь в тех точках, где производная равна нулю. Такие точки называются стационарными. Заметим, что если точка стационарна, то отсюда, вообще говоря, не следует, что в этой точке функция достигает экстремума, т.е. указанное необходимое условие экстремума функции не является достаточным (для f(x)=x³ в точке х=0 экстремума нет, однако ).

Теорема 1. (первое достаточное условие экстремума дифференцируемой функции).

Пусть функция y=f(x).

1) дифференцируема всюду в некоторой окрестности т. c.

2) т. c - стационарная, т.е. , тогда а) если существует окрестность, в которой производная положительна (отрицательна) слева от точки С и отрицательна (положительна) справа от точки С, то функция f(x) имеет в т. С локальный максимум (минимум) (рис. 1,2);

б) если же производная имеет один и тот же знак слева и справа от точки С, то экстремума в т. С нет (рис.3,4).

Рис.1 Рис.2 Рис.3 Рис.4

Доказательство. Докажем теорему для точки максимума. Пусть положительна в окрестности слева от точки С и отрицательна справа от точки С. . Обозначим через х₀ -любое значение аргумента из окрестности х₀>С. На сегменте [C,x₀] функция f(x) дифференцируема, следовательно, и непрерывна, поэтому по теореме Лагранжа

, (1)

где  - некоторое значение аргумента между точками С и х₀.

Аналогично рассматривается случай х₀<C.

При х₀>С , поэтому f(C)>f(x₀). Это и означает, что в точке С f(x) имеет локальный максимум.

Теорема 2. (второе достаточное условие экстремума).

Пусть функция y=f(x)

1) имеет производную всюду в некоторой окрестности т. С;

2) т. С - стационарная: (c)=0;

3) имеет конечную вторую производную в т. С.

Тогда, если , то в т. х=С f(x) имеет локальный максимум, если же то в точке х= С f(x) имеет локальный минимум.

Замечание. Теорема 2 не дает ответa о наличии экстремума в том случае, когда или не существует в т. х= С. В этом случае поведение функции в т. С следует изучить с помощью первого достаточного условия экстремума.

Пример. Найти экстремум функции Вычислим производную: Производная определена и дифференцируема на всей числовой оси. Найдем стационарные точки, решив уравнение . Рассматриваем делители свободного члена :  . Отсюда получаем корень х₁=-1.

Деля на х+1,получим:

Решая квадратное уравнение x2+2x-4=0, получим x2=-1+ , x3=-1- Итак, имеем:

Определим промежутки возрастания и убывания функции и исследуем функцию на экстремум.

x	(-, -1- )	-1-	(-1- ,-1)	-1	(-,-1+ )	-1+	(-1+ ,+)
	+	0	+	0	—	0	+
y		4				4
Рис.		лок. макс.		лок. мин.		лок. макс.

Пример 2. Найти экстремум функции . Находим производную . Стационарные точки х₁=0 и х₂=2. Вычислим . Так как ,

то в т. х=0 - локальный максимум, а в точке х=2- локальный минимум.