1 .1. Векторная алгебра Для замечаний
1. Основной текст
1.1. Векторная алгебра
1.1.1. Понятие вектора и линейные операции над векторами
1.1.1.1. Понятие вектора
Геометрическим вектором, или просто вектором, будем называть направленный отрезок.
Обозначать вектор
будем либо как направленный отрезок
символом
,
где точки A и B обозначают соответственно
начало и конец данного вектора, либо
символом
.
Начало вектора
называют точкой его приложения. Длину
вектора будем обозначать символом
модуля:
или
.
Вектор называется нулевым, если совпадают его начало и конец. Нулевой вектор имеет длину, равную нулю.
Векторы называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Два вектора называются равными, если они коллинарны, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными.
Точка приложения вектора может быть выбрана произвольно, поэтому изучаемые векторы называют свободными.
1.1.1.2. Линейные операции над векторами
Линейными операциями называют операцию сложения векторов и операцию умножения векторов на вещественные числа.
Определение 1.
Суммой
двух векторов
и
называется вектор, идущий из начала
вектора
в конец вектора
при условии, что вектор
приложен к концу вектора
.
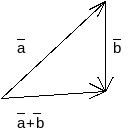
Это правило называют “правилом треугольника”.
Свойства сложения векторов:
1.
Доказательство. Приложим два произвольных вектора и к общему
началу 0. Обозначим через A и B концы векторов и соответственно и рассмотрим параллелограмм OBCA.
|
|
,
.
Из определения 1
и OAC
следует, что
,
а из OBC
видим, что
,
ч.т.д.
Замечание.
При доказательстве свойства 1 нами
получено правило сложения векторов,
называемое “правилом параллелограмма”:
если векторы
и
приложены к общему началу и на них
построен параллелограмм, то сумма
(
)
этих векторов представляет собой
диагональ этого параллелограмма, идущую
из общего начала векторов
и
.
2.
Доказательство.
Приложим вектор
к произвольной точке 0, вектор
к концу вектора
и вектор
к концу вектора
.
Обозначим буквами A, B, C концы векторов , и , тогда
,
ч.т.д.
3. Существует
нулевой вектор
такой, что
для любого вектора
.
Это свойство вытекает из определения
1.
4. Для любого вектора
существует противоположный ему вектор
-
такой, что
.
Для доказательства этого свойства определим вектор - , противоположный вектору , как вектор, коллинеарный вектору , имеющий с ним одинаковую длину и противоположное направление.
Взятая по определению 1 сумма вектора с таким вектором - дает нулевой вектор.
Определение 2.
Разностью
вектора
и вектора
называется такой вектор
,
который в сумме с вектором
дает вектор
.
Из определения 2 и из правила треугольника (определение 1) сложения векторов вытекает правило построения разности : разность приведенных к общему началу векторов и представляет собой вектор, идущий из конца вычитаемого вектора в конец уменьшаемого вектора .
Определение 3.
Произведением
(
)
вектора
на вещественное число
называется вектор
,
коллинеарный вектору
,
имеющий длину
,
и имеющий направление, совпадающее с
направлением вектора
в случае >0
и противоположное направлению вектора
в случае <0.
Свойства операции умножения вектора на число:
5.
.
При “растяжении” сторон параллелограмма в раз в силу свойств подобия диагональ также “растягивается” в раз, т.е.
.
6.
.
7.
.
Последние два свойства очевидны из геометрических соображений.