1.11. Ряды Для замечаний

1.11. Ряды

1.11.1. Числовые ряды

1.11.1.1. Основные понятия

Пусть задана некоторая бесконечная последовательность чисел:

U₁, U₂, ... , U_n, ... (1).

Составленный их этих чисел символ (формальное выражение)

U₁+U₂+ ... + U_n+ ... (2).

называется бесконечным чиловым рядом (или просто рядом). Вместо (2), пользуясь знаком суммы, часто пишут так:

(2а),

где символ  заменяет слово “сумма”, а индексы внизу и вверху означают, что нужно взять сумму чисел U_n, когда n пробегает все целочисленные значения от 1 до . (Впрочем, нумерацию членов ряда иногда бывает удобнее начинать не с единицы, а с нуля или же с какого - либо натурального числа, большего единицы).

Числа U₁, U₂, ... , U_n, ... называются членами ряда, а член ряда, стоящий на n-ом месте от начала, - его общим членом.

Примеры рядов:

1-1+1-1+... ,

a+aq+aq²+...+aq^n-1+... .

Задать ряд - это значит указать правило, закон образования его членов, по которому можно найти любой его член. Ряд можно задать формулой его общего члена. Например, если , то тем самым определен следующий ряд:

.

Выражение (2) является формальным, поскольку сумма бесконечного числа слагаемых не определена. Но поскольку в этом выражении между числами ряда знак суммирования, то подразумевается, что члены ряда как-то складываются. Сумма любого числа слагаемых будет найдена, если их складывать последовательно по одному. Это приводит к мысли поставить в соответствие ряду некоторое число и назвать его суммой ряда. С этой целью вводят понятие частичной суммы ряда.

Определение: Частичной суммой S_n числового ряда (2) называется сумма его первых n слагаемых, т.е.

S₁=U₁, S₂=U₁+U₂, S₃=U₁+U₂+U₃, ..., S_n=U₁+U₂+U₃+....+U_n.

Определение: Суммой числового ряда называется предел последовательности его частичных сумм, если этот предел существует

.

Если cуществует, то ряд (2) называется сходящимся, если же не существует, то ряд (2) называется расходящимся. В частности, если =, то ряд расходится.

Примеры:

1. Рассмотрим ряд 1-1+1-1+1-... . Найдем его частичные суммы S₁=1, S₂=0, S₃=1, S₄=0,... Последовательность его частичных сумм 1,0,1,0,1,0,... не имеет предела, следовательно, ряд расходится.

2. Рассмотрим ряд

.

Найдем его частичные суммы:

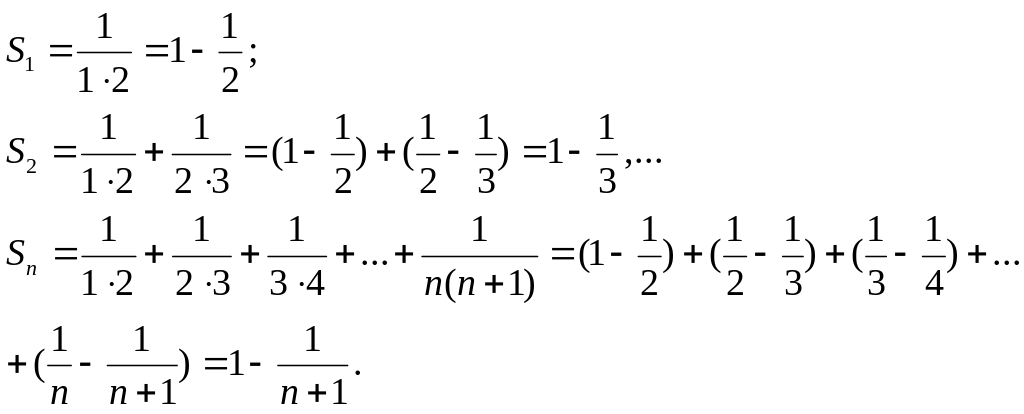
Так как , то рассматриваемый ряд сходится: его сумма равна 1.

3. Рассмотрим сумму членов геометрической прогрессии с первым членом а и знаменателем q (будем считать а0):

а+aq+aq²+aq³+...+aq^n-1+... .

Известно, что сумма S_n первых прогрессии определяется по формуле

или .

Рассмотрим несколько случаев в зависимости от величины q:

1. |q|<1. Тогда (т.к. ). Следовательно, при |q|<1 ряд сходится и его сумма .

2. |q|>1. Тогда |qⁿ| при n, поэтому S_n, т.е. не существует.

3. q=1. В этом случае ряд имеет вид а+а+а+...+а+... .

При этом S_n=n*a и , так как а0. Следовательно, ряд расходится.

4. q=-1. Тогда ряд имеет вид а-а+а-а+а-...(-1)^n-1а+... . Его частичные суммы попеременно ранвы а и 0: S₁=a, S₂=0, S₃=a, S₄=0, ..., но такая последовательность не имеет предела, и, следовательно, рассматриваемый ряд расходится.

Итак, ряд, составленный из членов геометрической прогрессии, сходится тогда и только тогда, когда знаменатель прогрессии q по абсолютной величине меньше единицы.