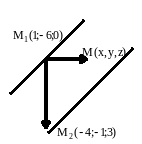2. Решение типовых задач контрольных работ Для замечаний

2. Решение типовых задач контрольных работ

Задание 1. Написать уравнение прямой, проходящей через две известные точки А(2;3) и В(6;-2) и вычислить длину отрезка АВ.

Решение. Уравнение прямой, проходящей через две известные точки М₁(x₁,y₁) М₂(x₂,y₂) имеет вид:

поэтому уравнение прямой (АВ) примет вид:

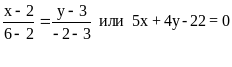
Расстояние между точками М₁ и М₂ определяется по формуле:

поэтому длина отрезка АВ:

.

Задание 2. Написать уравнение высоты (BN) и вычислить ее длину в треугольнике А(6;0), В(2;-3), С(-4;9).

Решение: Уравнение пучка прямых, проходящих через точку М(x₀,y₀) имеет вид : y-y₀=k(x-x₀).

Угловой коэффициент прямой (BN) найдем из того условия, что (ВN)(АС). Условие перпендикулярности двух прямых, имеющих угловые коэффициенты k₁, k₂:

.

Угловой коэффициент прямой, проходящей через точки М₁(x₁;y₁) и М₂(x₂;y₂) - ;

т.о.,

и уравнение (BN), следовательно, имеет вид :

Для вычисления высоты BN воспользуемся формулой, определяющей расстояние d точки М₀(x₀;y₀) до прямой, заданной уравнением Ax+By+C=0:

Нам нужно определить расстояние точки В(2;-3) до прямой, идущей через точки А(6;0) и С(-4;9).

Уравнение: (АС)

.

Задание 3. Вычислить в радианах величину внутреннего угла В в треугольнике А(4;-1), В(-4;-5), С(1;10).

Решение: Для определения угла В воспользуемся формулой тангенса

Рис. 2

угла между двумя прямыми, имеющими угловые коэффициенты k1 и k2: , где k1 - угловой коэффициент той прямой, которая поворачивается до совмещения со второй против часовой стрелки.

В нашем случае такой прямой является (ВА) (см. рис.2)

.

Задание 4. Написать уравнение (ВК) биссектрисы внутреннего угла треугольника с вершинами А(4;-1), В(-4;-5), С(1;5).

Рис. 3

Решение: Воспользуемся уравне- ниями биссектрис углов, образован- ных пересечением двух прямых, за- данных уравнениями:

Уравнения таких биссектрис имеют вид:

Точка М(x;y), координаты которой удовлетворяют этому условию, равноудалена от двух данных прямых, т.к. в левой и правой части равенства записаны расстояния ее до этих прямых.

В нашем случае уравнения прямых (АВ) и (ВС) имеют вид:

(АВ):

(BC):

Уравнения двух биссектрис угла В (внутреннего и внешнего) имеют вид:

, что равносильно уравнениям:

x-2y-6=2x-y+3 или y=-x-9 (1)

x-2y-6=-(2x-y+3) или x-y-1=0(2) и y=x-1(2)

Из уравнений (1), (2) угловые коэффициенты этих биссектрис

k=-1, k=1

Искомый угловой коэффициент должен удовлетворять неравенству:

k_(BA)< k_(BK) <k_(BC) , (см. рис.3)

Так как

и уравнение биссектрисы (ВК) есть x-y-1=0.

Задание 5. Составить уравнение линии, каждая точка которой вдвое дальше от прямой y+2=0, чем от точки F(-3;1).

Решение: Пусть точка М(x,y) обладает указанными свойствами:

Рис. 4

, где d - расстояние точки М до заданной прямой.

Координаты x, y точки М должны удовлетворять следующему уравнению:

После возведения в квадрат и соответствующих преобразований получим уравнение:

4x² + 24x + 3y² - 12y + 36=0 или

4(x² +6x +9 - 9) + 3(y² -4y +4 -4) - 36 = 0

----------- ------------

4(x + 3)² + 3(y-2)² - 48 + 36 = 0

Это уравнение эллипса с осями симметрии, параллельными координатным осям с центром в точке С(-3;2) и полуосями

Рис. 5

Задание 6. Составить уравнение гиперболы, симметричной относительно координатных осей, с фокусами на оси Ox, если уравнения ее асимптот , а расстояние между директрисами .

Решение: Уравнение такой гиперболы имеет вид и для его записи необходимо вычислить величины a и b. Так как уравнения асимптот гиперболы имеют вид , то для имеем соотношение:

(1)

Так как расстояние между директрисами равно , где  - эксцентриситет, то :

(2)

Кроме того, поэтому условие (2) можно записать так:

Для a и b получим следующую систему:

a=8, b=6 и уравнение гиперболы:

.

Задание 7. Даны вершины пирамиды: А₁ (2;-1;1), А₂ (5;5;4), А₃ (3;2;-1),

А₄ (4;1;3). Написать уравнение высоты А₄К, вычислить ее длину, вычислить объем пирамиды и площадь грани А₁ А₂ А₃ .

Решение: Каноническое уравнение прямой, проходящей через точку М(x₀ ;y₀ ;z₀) параллельно вектору имеет вид:

.

Поэтому канонические уравнения прямой, проходящей через точку А₄ (4;1;3) имеют вид:

, где вектор m;n;p- направляющий, т.е. параллельный искомой плоскости.

Т.к. (А₄ К)  плоскости (А₁ А₂ А₃), то нормальный вектор этой плоскости будет направляющим для искомой прямой. Уравнение плоскости, проходящей через точки А₁ (2;-1;1), А₂ (5;5;4), А₃ (3;2;-1) можно записать как условие компланарности векторов , где М(x;y;z) - любая точка плоскости.

Необходимым и достаточным условием компланарности этих векторов является равенство нулю их смешанного произведения:

.

Или в координатной форме:

Нормальный вектор плоскости (А₁ А₂ А₃) , а канонические уравнения высоты (А₄К):

.

Для вычисления длины высоты (А₄ К) воспользуемся формулой.

Расстояние d точки М₀ (x₀; y₀; z₀) до плоскости Ax+By+Cz+D=0

Площадь грани А₁ А₂ А₃ можно вычислить по формуле:

,

где - векторное произведение векторов.

Объем пирамиды вычислим по формуле:

- смешанное произведение векторов.

Задание 8. Составить уравнение плоскости, проходящей через две параллельные прямые:

.

Решение: Из канонических уравнений прямых видно, что первая идет через точку М1 (1; -6; 0), а вторая - через М2 (-4; -1; 3), и обе прямые имеют направленный вектор . Пусть точка М(x; y; z) принадлежит искомой плоскости, тогда вектора

должны быть компланарны, т.е. , что в координатной форме записывается равенством:

,

что и является уравнением заданной плоскости. Раскрывая определитель и приводя подобные члены получим: 9x-6y+25z -45=0 .

Задание 9. Найти

Решение. При х числитель и знаменатель этой дроби являются бесконечно большими функциями, такое отношение, условно обозначаемое символом , представляет собой неопределенность, для раскрытия которой нужно провести преобразования.

Разделим числитель и знаменатель почленно на наивысшую в данной дроби степень х (на х³):

Замечание. представляют собой бесконечно малые функции при х, т.е. их пределы равны 0.

Задание 10. Найти

При х0 числитель и знаменатель дроби являются бесконечно малыми функциями, такое отношение, условно обозначаемое символом , представляет собой неопределенность, для ее раскрытия сделаем следующие преобразования:

Задание 11. Найти

Для раскрытия такого вида неопределенности сделаем следующие преобразования:

Задание 12. Найти

Для раскрытия неопределенности проведем следующие преобразования:

При вычислении заданного предела мы воспользуемся следующим результатом, называемым “первым замечательным пределом”:

При этом под  подразумевается любая бесконечно малая функция.

Например: можно вычислить, используя этот же результат. Заменим х-1=t. При х1 новая переменная t0

Задание 13.

Найти:

а)

б)

Решение:

И в первом и во втором случае мы имеем дело с неопределенностью вида [1^], так как:

а)

б)

Для раскрытия такого вида неопределенностей можно воспользоваться следующей формулой:

Вычислим первый предел, пользуясь этой формулой:

Для вычисления второго предела воспользуемся непосредственно результатом, называемым “вторым замечательным пределом”:

где е - некоторое число, равное пределу числовой последовательности

e  2,72.

Для вычисления заданного предела сделаем следующие преобразования:

Выражение, выделенное в квадратные скобки при х имеет пределом е, а показатель степени при х имеет пределом , в чем не трудно убедится, разделив числитель и знаменатель на х.

Задание 14. Найти

В данном случае второй сомножитель представляет собой неопределенность, обозначаемую символом [ — ], поэтому и произведение является неопределенностью. Для ее раскрытия проведем такие преобразования

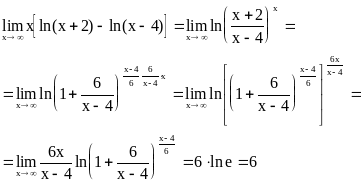
Задание 15. Дана функция:

исследовать ее непрерывность и схематически построить график.

Функция f(x) называется непрерывной в точке x₀, если

Любая элементарная функция непрерывна в своей области определения. Заданная нам функция у непрерывна в следующих интервалах: , т.к. в каждом из них задана элементарная функция: постоянная (-1), простейшая элементарная (-cosx), линейная .

Но в точках перехода от одной функции к другой, т.е. в точках x₁=0 и x₂= функция, хотя и определена, но может иметь разрыв, т.е. в этих точках могут быть нарушены условия непрерывности. Исследуем непрерывность функции у в точке х₁=0:

так как три полученных результата совпадают, условие непрерывности выполняется и у непрерывна в точке x₁=0.

Исследуем непрерывность функции в точке х₂=

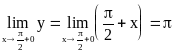
Несовпадение полученных результатов уже говорит о невыполнении условий непрерывности, и в точке х₂= функция имеет разрыв.

На рис. 8 схематически

Рис. 8

показан график функции у.

Задание 16. Найти производную функции y=cos(x²)

Решение: При вычислении производных пользуются таблицей производных основных элементарных функций и теоремой дифференцирования сложной функции:

пусть y=f(u) дифференцируема в точке u₀, u=f(x) дифференцируема в точке х₀, причем (х₀)=u₀, тогда сложная функция y=f((х)) дифференцируема в точке х₀ и

или .

В нашем случае u=x², y=cosu,

.

Задание 17. Найти производную функции y=lnsina^x

Решение: y=lnu, u=sinv, v=a^x,

тогда

.

Как видно из приведенных примеров, следует начинать дифференцирование с “внешней” элементарной функции, последовательно приближаясь к “внутренней”.

Задание 18. Найти производные функций:

а). б).

в).

Решение:

а).

б).

в).

Задание 19. Найти производную функции, заданной неявно:

x⁴+y²x+y⁷=0.

Решение. Правило вычисления производной функции, заданной неявно, заключается в том, что дифференцируют левую и правую часть равенства в предположении, что у есть функция от х:

Выражая из последнего равенства , получим:

Задание 20. Найти для функции, заданной параметрически:

Решение: Известна теорема о производной функции, заданной параметрически: пусть x=f(t) дифференцируема и

y=(t) - дифференцируемая функция, тогда производная или . При выполнении этого действия производная функции y(x) также выражена через параметр t.

;

Для отыскания производной второго порядка можно использовать тот же подход для функции заданной параметрически:

а в нашем случае

тогда

В нашем случае:

Можно использовать и готовую формулу для вычисления производной второго порядка функции

Задание 21.

Провести полное исследование функции и построить ее график.

Решение.

Исследование функции будем проводить по следующей схеме:

1.) Найдем область определения функции и точки пересечения ее графика с осями координат;

2.) Выясним четность (или нечетность) функции (если она задана на симметричном промежутке);

3.) Выясним периодичность функции;

4.) Исследуем функцию на непрерывность, найдем точки разрыва и выясним характер разрывов;

5.) Найдем асимптоты графика функции;

6.) Исследуем функцию на экстремум, найдем интервалы монотонности функции;

7.) Найдем точки перегиба и интервалы выпуклости и вогнутости графика функции.

Исследуем функцию по приведенной схеме.

1.) Функция определена при всех значениях х, для которых х²-1>0 или х>1, т.е. при - < x < -1 и +1 < x < +

C осью ОХ график функции пересекается в точке (х  1,25; 0).

С осью ОУ график функции не пересекается.

2.) Функция не является ни четной, ни нечетной.

3.) Функция не является периодической.

4.) На интервале (-; -1) и (+1; +) функция непрерывна.

5.) Вертикальные асимптоты:

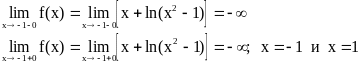
— две вертикальные асимптоты.

Ищем наклонные асимптоты:

Следовательно, ни наклонных, ни горизонтальных асимптот нет.

6.) Находим производную данной функции: . Производная существует и конечна во всех точках области определения функции. Следовательно, стационарные точки могут быть лишь в “нулях” производной:

В точке x₂=-1+ функция не определена. Следовательно, имеется только одна критическая точка х₁=-1- , принадлежащая области определения функции.

В интервале (-; -1- ) производная , а в интервале (-1- ; -1) . Следовательно, точка х=-1- точка максимума и . В интервале (-; -1- ) функция возрастает, а в интервале (-1- ; -1) - убывает. В интервале (1, ) производная и, следовательно, функция возрастает.

7.) Находим вторую производную функции

Значение на всей области определения функции. Следовательно, кривая везде выпукла и точек перегиба не имеет.

Внесем теперь результаты исследования в таблицу, а затем построим график (рис. 9) функции.

Замечание:

Таблицу можно заполнять постепенно, по мере исследования функции.

x				-1	1
y	+ — вып.	0 — мax. -0,84	— — вып.	верт. ас.	верт. ас.	+ — вып.

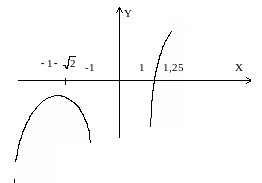
Рис. 9

Задание 22. Найти частные производные функции

Решение: Если переменная z зависит от двух и более независимых переменных x, y, ......., u, v, то z=f(x, y, ..., u, v) называют функцией нескольких независимых переменных. Важнейшим понятием в теории функций нескольких переменных является понятие частной производной. Частная производная функции z по данной переменной, например по у, обозначается одним из символов (не путать с обозначением производной для функции одной переменной ) и вычисляется в предположении, что все остальные переменные являются зафиксированными, т.е. их следует рассматривать как константы. Рассмотрим пример нахождения частных производных от заданной функции нескольких переменных (в частности, двух) переменных.

,

.