1.12. Дифференциальные уравнения Для замечаний

1.12. Дифференциальные уравнения

Обыкновенным дифференциальным уравнением n-го порядка называется выражение вида f(x,y,y',y'', ... ,y⁽ⁿ⁾)=0 или , то есть уравнение, содержащее неизвестную, а следовательно искомую функцию y=y(x) под знаком производной или дифференциала n-го порядка и других порядков k<n.

Пример. y'=f(x,y), .

Исходя из определения дифференциального уравнения следует, что его порядок равен порядку старшей производной, содержащейся в нем.

Степенью дифференциального уравнения называется степень старшей производной, содержащейся в нем.

Пример. (y''')²+(y')³=x⁴ - это дифференциальное уравнение третьего порядка, второй степени.

Решением дифференциального уравнения называется любая функция, которая будучи подставлена в это уравнение, обращает его в тождество.

Пример. y'=x - решение, - тоже.

Процедура отыскания решения называется интегрированием дифференциального уравнения.

Если задачу об отыскании всех решений дифференциального уравнения удается свести к вычислению конечного числа интегралов и производных от известных функций и к алгебраическим операциям, то говорят, что уравнение интегрируется в квадратурах.

Пример. Уравнение y'+y²=x^ интегрируется при =-4n(2n-1), где n-целое и =-2, во всех остальных случаях не интегрируется.

1.12.1. Геометрическая интерпретация дифференциальных уравнений

Пусть y=y(x) есть решение уравнения y'=f(x,y). Геометрически это значит, что в прямоугольных координатах касательная к кривой y=y(x) имеет в каждой, лежащей на ней, точке М(x,y) угловой коэффициент k=f(x,y). Таким образом, нахождение решений y=y(x) геометрически сводится к такой задаче: в каждой точке некоторой области на плоскости задано "направление", требуется найти все кривые, которые в любой своей точке М имеют направление, заранее сопоставленное этой точке. Если функция f(x,y) непрерывна, то это направление меняется при перемещении точки М непрерывно, и можно наглядно изобразить поле направлений, проводя в достаточно большом числе достаточно густо расположенных по всей рассматриваемой области точек короткие черточки с заданными для этих точек направлением.

На рис. 1 это выполнено для уравнения y'=y². Рисунок позволяет сразу представить себе, как должны выглядеть графики решений - интегральные кривые. Вычисление показывает, что решение данного уравнения есть уравнение . На рис. 1 вычерчены интегральные кривые, соответствующие значениям параметра с=0 и с=1.

1.12.2. Общий и частный интегралы. Общее и частное решения

Рассмотрим некоторую функцию y=(х,с), где с есть некоторый параметр или произвольная постоянная. Найдем дифференциальное уравнение, которому эта функция удовлетворяет. С этой целью возьмем производную от функции y, получим

y'='(х,с).

Если в этой операции будет исключено с, т.е. получается

y'=(x),

то это и будет дифференциальным уравнением первого порядка, разрешенным относительно производной, а y=(х,с) является его решением. Очевидно, в этом случае зависимость y от с линейна, т.е.

y=(х)+c.

Но допустим, что в '(х,с) содержится с. Тогда выражение y'='(х,с) нельзя назвать дифференциальным уравнением (ввиду неопределенности с) до тех пор, пока из выражения y'='(х,с) не исключим с.

Для этого разрешим уравнение y=(х,с) относительно с: с=(х,с). Это возможно, если функция (х,с) имеет отличную от нуля производную по с (по теореме о существовании обратной функции), т.е.

.

Пусть это условие выполнено. Тогда, подставив с=(х,с) в выражение y'='(х,с), получим y'='(х,(х,с)) - искомое дифференциальное уравнение, решением которого будет y=(х,с). Итак, функция, зависящая от одной произвольной постоянной y=(х,с), тогда является общим решением дифференциального уравнения, когда выполнено условие: . Слово "общее" означает, что все частные функции, удовлетворяющие уравнению y'='(х,(х,с)) могут быть получены из функции y=(х,с) приданием с определенных значений.

Пусть дана неявная функция одной переменной (х,y,с)=0, содержащая одну произвольную постоянную. Найдем дифференциальное уравнение, для которого эта неявная функция будет решением. Для этого продифференцируем (х,y,с)=0. Получим . Разрешая (х,y,с)=0 относительно с=(x,y) и подставляя его в уравнение , получим искомое дифференциальное уравнение

Решение дифференциального уравнения первого порядка, записанное в виде (х,y,с)=0, зависящее от произвольной постоянной, является общим интегралом. Рассмотрим теперь неявную функцию от одной переменной и n произвольных постоянных

(х,y,с₁,с₂, ... ,с_n)=0 (*)

Получим дифференциальное уравнение, для которого эта функция будет решением. Допустим, что (х,y,с₁,с₂, ... ,с_n) имеет производные по переменным x и y, n-го порядка. Дифференцируя (х,y,с₁,с₂, ... ,с_n)=0 n раз, получим

(**)

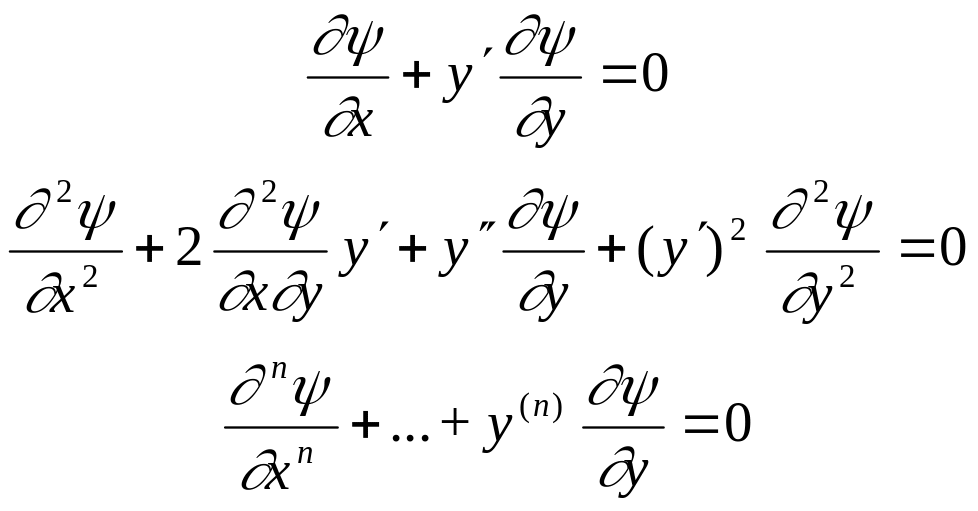Рассмотрим совместно выражения (*) и (**). Объявим в этих выражениях неизвестными с₁,с₂, ... ,с_n. Тогда (*) и (**) составляют систему n+1 уравнений, из которых можно исключить n произвольных постоянных. В результате получим уравнение n-го порядка

F(х,y,y',y'', ... ,y⁽ⁿ⁾)=0.

Выражение (*) является общим интегралом этого уравнения. Функция (*) называется общим интегралом уравнения тогда, когда после n-кратного дифференцирования образуется система конечных уравнений (*) и (**), допускающая существование единственного решения для постоянных с₁,с₂, ... ,с_n. Если (*) можно разрешить относительно y=(х,с₁,с₂, ... ,с_n), то получим общее решение уравнения.

Частным интегралом или частным решением дифференциального уравнения называется общий интеграл или общее решение, для которых указаны конкретные значения произвольных постоянных. Для определения произвольных постоянных необходимо задать столько условий, сколько постоянных. Эти условия включают задание значений функции и ее производных в определенной точке. Так для уравнения n-го порядка необходимо задать

.

Числа называются начальными значениями, эти равенства - начальными условиями.