2. Линейные группы

Существуют группы, состоящие не из всех биекций некоторого множества Х, а сохраняющие некоторую структуру, определенную на множестве Х.

Различные группы матриц относительно операции умножения называются линейными группами.

Пример 1. Множество G L_n(K) всех невырожденные матриц размера

n х n над полем Р с умножением матриц в качестве групповой операции при

n ≥ 2 образует абелеву группу. Она называется общей линейной группой.

Действительно, произведение двух невырожденных матриц будет невырожденным. ¹

Нейтральным элементом будет единичная матрица, которая является невырожденной, так как ее определитель всегда равен 1.

Всякая невырожденная матрица обладает обратной матрицей, также невырожденной, так как определитель обратной матрицы вычисляется как:

где det A ≠ 0.

Наконец, закон ассоциативности, выполняясь для всех матриц, справедлив, в частности, для матриц невырожденных.

Пример 2 Специальная линейная группа

SLn(K)={M GLn(K)| det M=1}

Пример 3. Множество квадратных вещественных симметрических матриц фиксированного порядка образуют группу с групповой операцией сложения.

Так как при сложении любых двух симметрических матриц всегда получаем только симметрическую матрицу, то групповая операция сложения не выводит элементы за пределы группы.

Ассоциативность выполняется в силу ассоциативности сложения. Единичный элементом является нулевая матрица. Обратным элементом для матрицы А является, очевидно, матрица –А, тоже симметрическая. Коммутативность также выполнена в силу коммутативности операции сложения.

Поэтому множество квадратных вещественных симметрических матриц фиксированного порядка образуют группу с групповой операцией сложения образуют абелеву группу.

Пример 4. Группа верхних треугольных матриц образует группу относительно операции умножения матриц.

Заметим, что ассоциативность умножения матриц следует из общей ассоциативности умножения, нейтральным элементом является единичная матрица, а обратным – обратная, которая существует для любой квадратной матрицы и находится по формуле АА^-1 = Е. Остается доказать, что умножение двух верхних треугольных матриц снова дает верхнюю треугольную матрицу. А это действительно так, поскольку каждый элемент матрицы-перемножения двух матриц

ищется по формуле

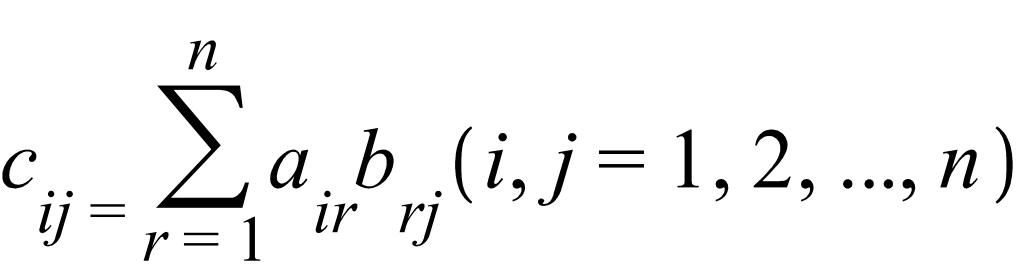
А так как суммироваться будут только ненулевые элементы, то матрица – произведение будет иметь такой же вид, как и исходные.

Пример 5

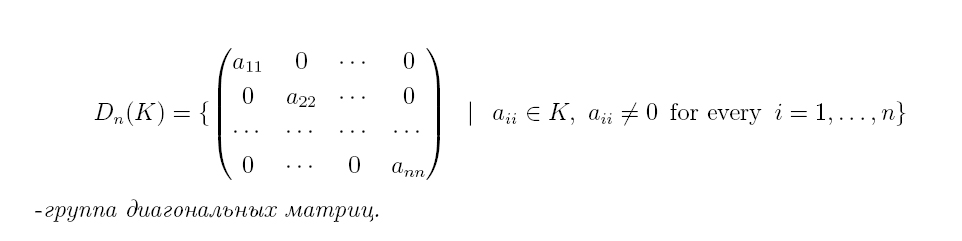
3. Группы движений

Движением (перемещением) плоскости называется такое преобразование, которое сохраняет расстояния. Другими словами, преобразование F называется перемещением, если для любых двух различных точек А и В плоскости справедливо соотношение | АВ | = | А'В' |, где А' = F (А) и B' = F(B).

Рассмотрим плоскость с введенной на ней метрикой ρ. Биективное отображение φ: R^2→ R² называется движением (изометрией), если оно сохраняет расстояния:

Пример 1. Множество движений плоскости образуют группу Isom (R²) с операцией композиции отображений образует группу движений плоскости. Нейтральный элемент – тождественное отображение, обратный – обратное отображение. Композиция ассоциативна.

Пример 2. Пусть F – произвольная фигура на евклидовой плоскости. Множество всех движений евклидовой плоскости, переводящих F на себя, с операцией «композиция двух движений», является группой. Эта группа называется группой симметрий фигуры F.

В группе симметрий правильного n – угольника имеется ровно 2n элементов: n вращений по часовой стрелке на углы

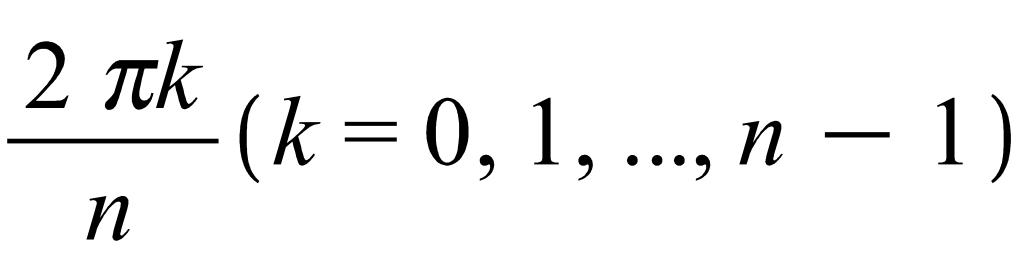
Вокруг его центра и n отражений относительно прямых, проходящих через центр и одну из его вершин или середину одной из его сторон. Все вращения в группе симметрий правильного n-угольника образуют подгруппу, которая называется группой вращения данного n-угольника.

Пример 3. Множество взаимно однозначных отображений множества Х на себя образует группу относительно операции композиции

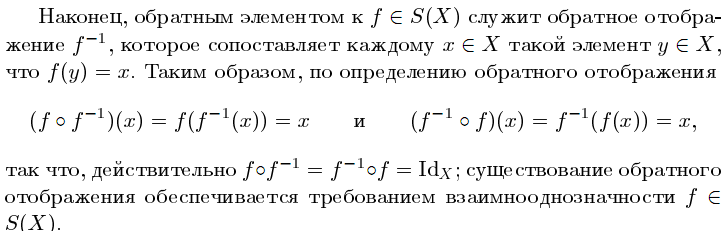
Пример 4. Множество самосовмещений n-угольного диэдра

Диэдр состоит из правильной n-угольной пирамиды и ее зеркального отражения в плоскости основания. Группа самосовмещений диэдра состоит из поворотов оси пирамиды (на углы 0, _{, …,} ) и так называемых опрокидываний, т.е. поворотов на угол π вокруг каждой из осей симметрии основания диэдра, т. е. правильного многоугольника, являющегося

общим основанием обеих пирамид, составляющих диэдр. Таких осей симметрии имеется n, так что перемещений второго рода имеется тоже n.

Число всех полученных перемещений есть, таким образом, 2n.

Всякое совмещение диэдра с самим собой должно либо оставлять

на месте точки S и S' (самосовмещения первого рода), либо менять их местами (самосовмещения второго рода). Основание диэдра должно переходить при таком перемещении в самого себя.

Заметим, что произведение (т. е. последовательное осуществление) двух самосовмещений первого рода дает самосовмещение первого рода, произведение самосовмещений первого рода с самосовмещениями второго рода дает самосовмещение второго рода, а произведение двух самосовмещений второго рода дает самосовмещение первого рода.

При этом произведение двух самосовмещений, из которых одно — первого, а другое — второго рода, зависит от порядка сомножителей: если а — самосовмещение первого, а b — самосовмещение второго рода, то аb = ba^-1.

При самосовмещениях первого рода основание переходит в само себя, оставаясь в своей плоскости; оно испытывает, таким образом, поворот на один из углов: 0, _{, …,} .

Таким образом, и все перемещение диэдра оказывается поворотом вокруг оси диэдра на тот же угол. Итак, самосовмещений первого рода имеется (включая тождественное самосовмещение, т. е. покой) ровно n.

Эти самосовмещения суть не что иное, как повороты диэдра вокруг его оси на углы 0, _{, …,} .

Пусть дано некоторое вполне определенное самосовмещение второго рода, т. е. такое самосовмещение диэдра с самим собой, при котором вершины S и S' меняются местами.

Произведем после данного самосовмещения второго рода некоторое вполне определенное опрокидывание диэдра, т. е. перемещение, заключающееся в повороте диэдра на угол π вокруг одной какой-нибудь зафиксированной оси симметрии основания. Получим cамосовмещение первого рода (произведение двух самосовмещений второго рода есть самосовмещение первого рода.), т. е. поворот диэдра вокруг его оси.

Итак, всякое самосовмещение второго рода переходит после одного и того же опрокидывания в некоторое самосовмещение первого рода. Отсюда следует легко: всякое самосовмещение второго рода можно получить, производя (до или после некоторого самосовмещения первого рода) одно и то же опрокидывание.

Отсюда, далее следует, что число самосовмещений второго рода равно числу самосовмещений первого рода.т. е. n.

С другой стороны, ясно, что все опрокидывания являются самосовмещениями второго рода. Так как этих опрокидываний имеется ровно n, то ими, очевидно, и исчерпывается вся совокупность самосовмеще-

ний второго рода.

Таким образом, группа самосовмещений n-угольного диэдра есть некоммутативная группа порядка 2n, состоящая из n поворотов вокруг оси диэдра SS' и из n опрокидываний, т. е. поворотов на угол π вокруг осей симметрии основания диэдра. Все n опрокидываний получаются умножением одного из них на n поворотов диэдра вокруг его оси SS'.