2. Бесконечные абелевы группы

Согласно определению бесконечной абелевой группы, можно выделить следующие примеры подобных групп.

Элементарные примеры:

1. Любое (бесконечное) кольцо – абелева группа относительно операции сложения.

2. Любое (бесконечное) поле без нуля – абелева группа относительно операции умножения ( т. к. все его ненулевые элементы образуют коммутативную группу по умножению).

3. Группы, возникающие в числовых структурах относительно операции сложения – это, например: 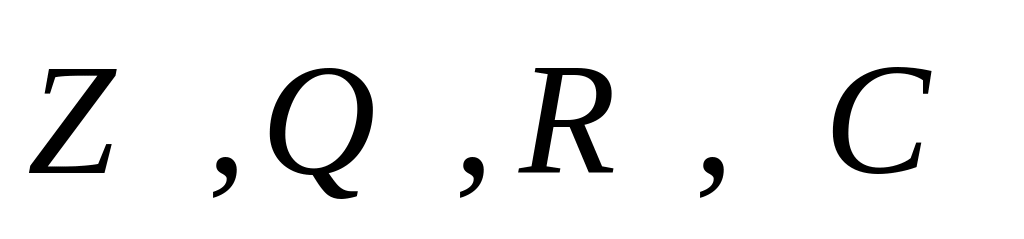. Это - абелевы бесконечные группы.

4. Группы, возникающие в числовых структурах относительно операции умножения – это, например: . Это - абелевы бесконечные группы.

Пример 1. Вращения на плоскости.

Пусть множество Ф – множество всех поворотов на угол φ.

При сложении двух углов φ₁ и φ₂ из Ф получаем угол φ₃ опять же из множества Ф φ₁+ φ₂= φ₃. Таким образом, операция вращения на плоскости обладает групповым свойством. Проверим аксиомы группы для данной операции.

1. Ассоциативность: (φ₁+ φ₂)+ φ₃= φ₁+ (φ₂+ φ₃)

2. Нейтральный элемент в этом случае – поворот на угол 0 (+ 2πn)

3. Обратным элементом является поворот на угол (– φ) (+2πn)

4. Коммутативность: φ₁+ φ₂ = φ₂+ φ₁

Итак, вращения вокруг оси, перпендикулярной выбранной плоскости, образуют абелеву группу.

Пример 2. Множество векторов трехмерного пространства

Действительно, для любых векторов а, b, с векторного пространства выполняется групповое свойство, так как при сложении двух векторов снова получается вектор. Аксиомы группы:

1. Ассоциативность: (a + b) + c = a + (b + c)

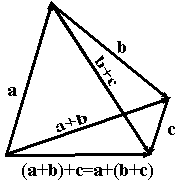
2. Нейтральный элемент: нулевой вектор 0 т.,ч. a + 0 = a

3. Обратный элемент: a + (-a) = 0

4. Коммутативность: a + b = b + a

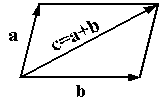
Таким образом, множество векторов трехмерного пространства образуют абелеву группу по сложению.

Пример 4. Кольцо является абелевой группой по сложению (из определения кольца), обратимые ненулевые элементы любого поля по умножению также составляет абелеву группу.

3. Конечные неабелевы группы

Конечная группа называется неабелевой, если не выполняется аксиома коммутативности. Рассмотрим следующие примеры конечных неабелевых групп.

Пример 1. Множество всех невырожденных матриц порядка n над полем Р с операцией умножения образует группу. Действительно, произведение двух невырожденных матриц будет невырожденным, единичная матрица является невырожденной, всякая невырожденная матрица обладает обратной матрицей, также невырожденной, закон ассоциативности, выполняясь для всех матриц, справедлив, в частности и для невырожденных.

Пример 2. Множество квадратных матриц порядка n, в каждой строке и каждом столбце которых ровно один ненулевой элемент, равный ± 1, относительно умножения.

В самом деле, умножение подобных матриц, снова дает матрицу из группы:

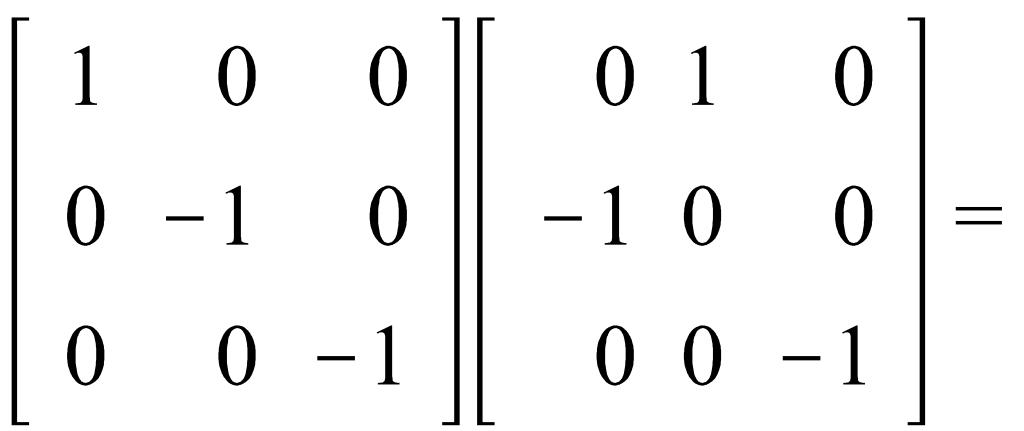
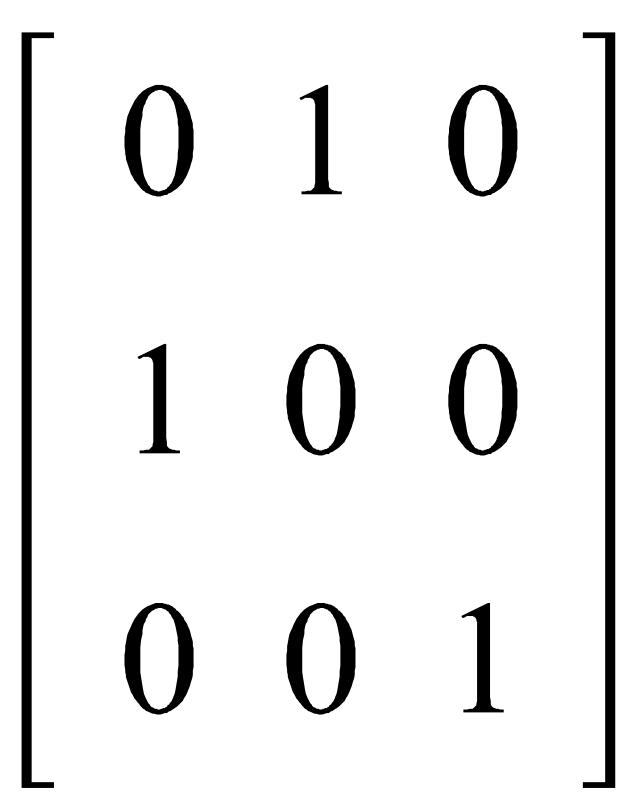
Проверим аксиомы группы:

1. Ассоциативность:

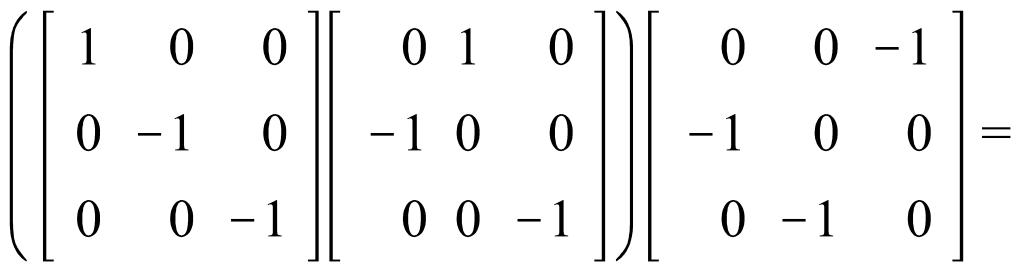
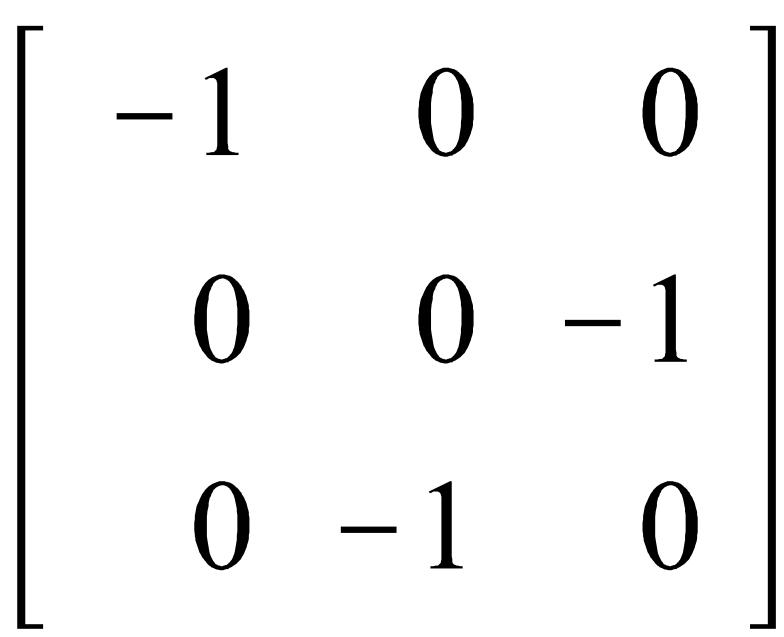
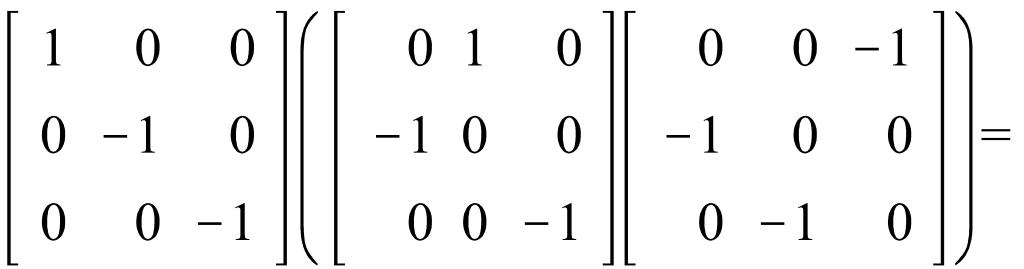
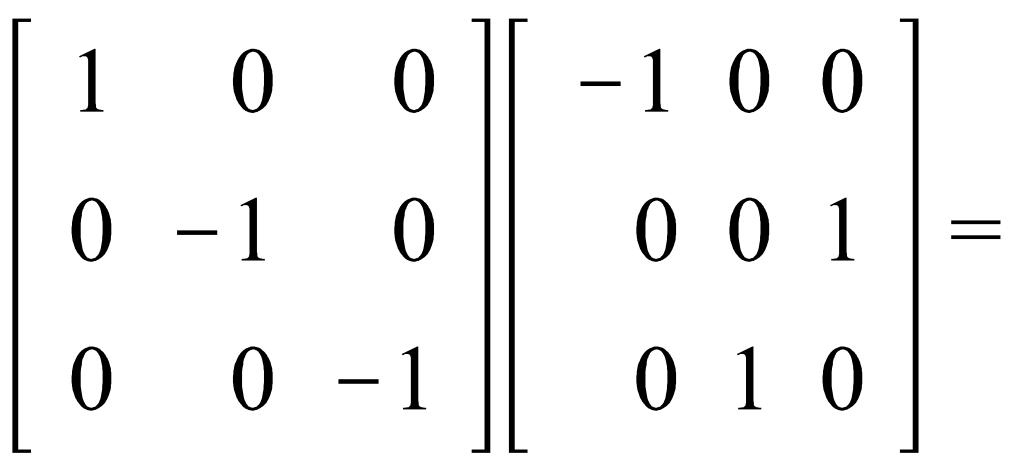
2. Нейтральный элемент: единичная матрица (принадлежит данной группе)

3. Обратный элемент: обратная матрица также будет принадлежать данной группе, так как определитель любой матрицы из группы равен ± 1, алгебраическое дополнение будет равно либо 0, либо 1.

4. Коммутативность не выполняется:

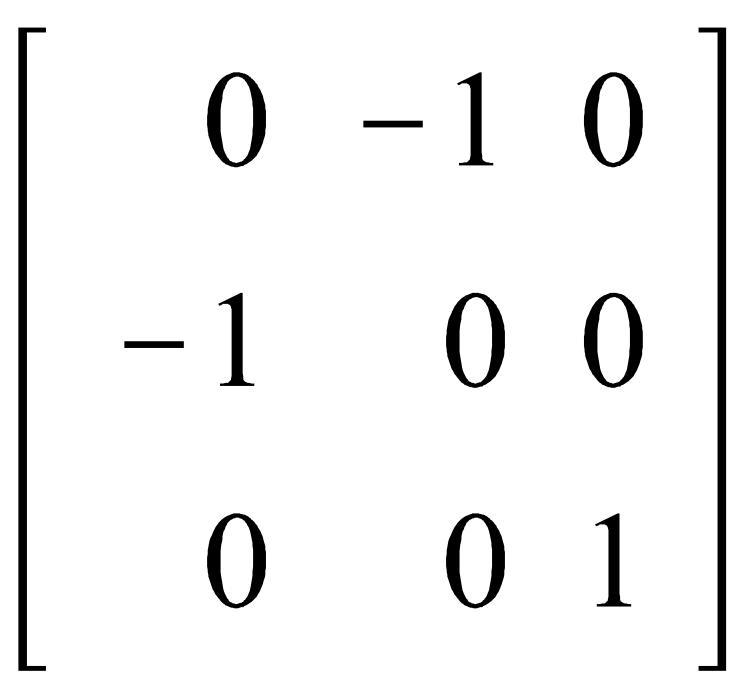
Пример 3. Совокупность четных подставок n- ой степени составляет по умножению группу, притом конечного порядка ½ n!

Четность подстановки совпадает с четностью числа транспозиций, входящих в разложение этой подстановки в произведение транспозиций. Поэтому произведение двух четных подстановок само четно: в самом деле, представление АВ в виде произведения транспозиций мы получим, записав соответствующие разложения для А и В одно за другим.

Путем проверки можно выяснить, что умножение будет ассоциативным. Четность тождественной подстановки очевидна. Наконец, четность подстановки А-1 при четной А следует хотя бы из того, что записи этих подстановок можно получить одну за другой переменой мест верхней и нижней строк, т.е. они содержат равное число инверсий.