1. Типы групп

Все группы условно можно разделить на типы в соответствии со схемой.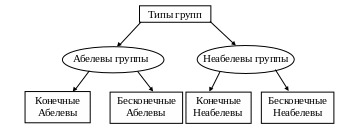

1. Конечные абелевы группы

Согласно определению конечной абелевой группы, можно выделить следующие примеры подобных групп.

Элементарные примеры:

1. Элементы е, а со законом композиции

образуют абелеву группу.

2. Любое конечное кольцо – абелева группа относительно операции сложения.

3. Любое конечное поле без нуля – абелева группа относительно операции умножения.

Пример 1. Пусть (M, ∙) – группа и а ∈ M. Определим на М новую бинарную операцию * по правилу:

x * y = xay (x, y ∈ M)

Тогда (M, *) – абелева группа. В самом деле,

1. ассоциативность: (x * y) * z = (xay) * z = xayaz

x * (y * z) = x * (yaz) = xayaz

2) нейтральный элемент: a^-1

x * a^-1 =xaa^-1 = x

3) обратный элемент: x^-1

x * x^-1 =xax^-1 = a

4) коммутативность:

x * y = y * x = xay

Пример 2. Группа классов вычетов целых чисел по модулю n относительно операции сложения n – Z/nZ (циклическая группа порядка n), где n конечно

Зафиксируем натуральное число n и рассмотрим множество остатков от деления каждого натурального числа на n. Ясно, что различных остатков ровно n, они равны 0, 1, 2, …, n-1.

Разобьем множество Z на n классов по следующему принципу:

0. в нулевой класс соберем все такие числа, которые при делении на n дают остаток 0, т.е. целиком делятся на n;

1. в первый класс соберем числа которые при делении на n дают остаток 1;

…

n - 1) в (n - 1) класс соберем все такие числа, которые при делении на n дают остаток n-1

Теперь определим бинарную операцию ○ на множестве Z_n построенных классов. Пусть (k) и (m) – два класса. Выберем из них по числу: а = k (mod n),

b = m (mod n). Тогда a + b = k + m (mod n). Таким образом,

(k) ○ (m) =

Множество Z_n относительно операции ○ образует группу, называемую группой вычетов по модулю n. Все групповые свойства выполнены: какие бы элементы группы мы не взяли, результат последовательного применения операции снова попадет в нашу группу, операция ○ ассоциативна, т.к. сводится к операции сложения чисел, нейтральным элементом служит нулевой класс (0), элементом, противоположным классу (k), является класс (n - k). Очевидно, что операция будет коммутативной.

Пример 3. Корни n-ой степени из единицы по умножению.

Возьмем в поле комплексных чисел совокупность корней n-ой степени из единицы.

Произведение двух корней n-ой степени из единицы само есть корень n-ой степени из единицы. Действительно, пусть εⁿ = 1 и ηⁿ = 1. Тогда

(εη) ⁿ= εⁿ ηⁿ =1. Таким образом, произведение корней обладает групповым свойством. Докажем аксиомы группы.

1. Ассоциативность следует из того, что умножение комплексных чисел ассоциативно

2. Нейтральным элементом будет служить 1, которая, разумеется, принадлежит данному множеству.

3. Число, обратное корню n-ой степени из единицы, само есть такой же корень.

Действительно, если εⁿ = 1, то ε ε^-1= 1, а значит, εⁿ (ε^-1) ⁿ = 1, то есть

(ε^-1) ⁿ = 1.

4. Коммутативность следует из коммутативности умножения комплексных чисел.

Таким образом, корни n-ой степени из единицы составляют по умножению абелеву группу, притом конечного порядка n.

Пример 4. Совокупность двоичных n-символьных комбинаций образует группу из 2ⁿ элементов, если в качестве групповой операции используется посимвольное сложение по модулю 2. Так, если а = (101110), b = (111011), то с = а + b = (010101). Нейтральным является элемент (000000), а обратным является сам элемент, так как 110010 + 110010 = 000000

Пример 5 Всевозможные повороты правильного треугольника вокруг его центра О.

Доказательство:

Два поворота считаются совпадающими, если они отличаются друг от друга на целое число полных оборотов (т.е. на кратное 360°). Несложно видеть, что среди всех поворотов треугольника лишь три поворота переводят треугольник в себя, а именно: повороты на 120°, 240° и нулевой поворот, оставляющий все вершины, а следовательно, и все стороны треугольника на месте. Первый поворот переводит вершину А в вершину В, вершину В в вершину С, вершину С в вершину А (он перемещает, как говорят, вершины А, В, С в циклическом порядке). Второй поворот перемещает А в С, В в А, С в В (т. е. перемещает в циклическом порядке А, С, В).

Пусть умножить два поворота —значит, последовательно произвести их один за другим.

Таким образом, поворот на 120°, умноженный с самим собой, дает поворот на 240°, умноженный с поворотом на 240° дает поворот на 360°, т. е. нулевой поворот. Два поворота на 240° дают поворот на 480° = 360° + 120°, т. е. их произведение есть поворот на 120°.

Если обозначить нулевой поворот через а₀, поворот на 120° через а₁ поворот на 240° через а₂, то получим следующие соотношения:

а₀ • а₀ = а₀, а₀ • а₁ = а₁ • а₀ = а₁,

а₀ • а₂ = а₂ • а₀ = а₂, а₁ • а₁ = а₂,

а₁ • а₂ = а₂ • а₁ = а₀, а₂ • а₂ = а₁.

Итак, для каждых двух поворотов определено их произведение. Это умножение удовлетворяет аксиоме ассоциативности. Действительно,

(а₀ • а₁)• а₂ = а₁ • а₂= а₀

а₀ • (а₁• а₂) = а₀ • а₀ = а₀

Среди поворотов имеется также нулевой поворот а₀, который удовлетворяет условию

а • а₀ = а₀ • а = а

для любого поворота а.

Также каждый из трех поворотов имеет обратный ему поворот, дающий в произведении с данным поворотом нулевой поворот: нулевой поворот, очевидно, обратен самому себе, а₀^-1= а₀, так как а₀ • а₀ = а₀, тогда как а₁^-1 = a₂ и а₂^-1 = a₁ (так как a₁ • a₂ = а0).

Из определения следует, что умножение поворотов удовлетворяет коммутативности. Действительно,

а₀ • а₁ = а₁ • а₀ = а₁,

а₀ • а₂ = а₂ • а₀ = а₂,

а₁ • а₂ = а₂ • а₁ = а₀

Итак, умножение поворотов правильного треугольника, удовлетворяет всем перечисленным аксиомам абелевой группы.

Пример 6 Группа самосовмещений правильного n-угольника.

Доказательство:

Самосовмещением данной геометрической фигуры F назовем такое движенние плоскости или пространства,  которое переводит F в себя, т. е. совмещает фигуру F с собой. Пусть дан в плоскости правильный многоугольник . Требуется найти те движения плоскости, которые совмещают его с самим собой. При этом перемещении всякая вершина многоугольника должна перейти в вершину, всякая сторона - в сторону, а центр многоугольника – в себя, ибо он один.  Пусть при некотором  перемещении вершина перейдет, положим, в .  Тогда сторона должна перейти либо в сторону либо в сторону . Но если бы сторона перешла в сторону , то треугольник перешел бы в треугольник .  Этот последний треугольник можно было бы, передвигая его в плоскости, перевести в положение , являющееся зеркальным отражением треугольника относительно стороны . В результате оказалось бы, что мы треугольник перемещением в его плоскости перевели в его зеркальное отражение, а это невозможно. Итак, сторона должна перейти в сторону . Точно таким же образом мы убеждаемся в том, что сторона переходит в , сторона переходит в и т. д. Другими словами, наше перемещение есть поворот многоугольника в его плоскости на угол   Введём операцию композиции поворотов: , которая сводится к тому, что углы поворотов складываются. Еще надо заметить, что два поворота, отличающиеся друг от друга на целое число полных углов , оказывают на наш многоугольник (как, впрочем, и на всю плоскость) одинаковое действие, и потому будут отнесены в один класс поворотов. Т.е., нас будет интересовать не величина угла поворота, а остаток от деления этого угла на . Классом поворотов назовем множество поворотов на углы вида , где . Классы поворотов правильного n-угольника  образуют группу по операции : 1. Нейтральным элементом является – класс поворотов на . 2. Обратным элементом для  класса является класс поворотов . 3. Асооциативность очевидна, так как операция определена через сложение чисел. Остается заметить, что и в этой группе любой ее элемент может быть получен последовательным применением поворота на угол . Это означает, что группа вращений правильного n-угольника циклична.

Пример 6 Совокупность всех самосовмещений фигуры F с операцией произведения самосовмещений.

Доказательство:

Пусть в пространстве или на плоскости дана фигура F. Рассмотрим все самосовмещения этой фигуры, то есть все перемещения её (в пространстве или на плоскости), совмещающие эту фигуру с нею самой.

В качестве произведения двух самосовмещений и определим перемещение, возникающее в результате последовательного совершения сначала перемещения , а потом перемещения . Очевидно, что перемещение также является совмещением фигуры F с собой, в предположении, что перемещения и порознь являются таковыми. Совокупность всех самосовмещений фигуры F с только что определенной операцией произведения образует группу. В самом деле, умножение перемещений удовлетворяет условию ассоциативности; далее, в совокупности самосовмещений имеется единичное, или тождественное, самосовмещение (то есть перемещение, оставляющее каждую точку фигуры на месте). Наконец, к каждому самосовмещению g имеется обратное ему самосовмещение (передвигающее каждую точку назад, в исходное положение, из положения, которое оно заняло после перемещения g).

Пример 7 Группа поворотов правильной n-угольной пирамиды (вокруг ее оси).

Доказательство:

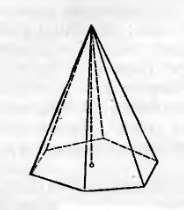
Очевидно, что группа поворотов правильной n-угольной пирамиды вокруг ее оси изоморфна группе поворотов правильного n-угольника, лежащего в ее основании; эта группа есть, таким образом, циклическая группа порядка n. Легко убедиться, что поворотами пирамиды вокруг оси (на углы ) исчерпываются все перемещения, совмещающие пирамиду.