10.1. Кинетическая энергия твердого тела при различных
Движениях
Поступательное движение. Кинетическая энергия твердого тела при его поступательном движении равна половине произведения массы тела на квадрат его скорости.
,
где т – масса тела.
Вращение твердого тела вокруг неподвижной оси. Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения его момента инерции относительно оси вращения на квадрат угловой скорости тела (рис. 3.63).
Плоское движение твердого тела. Кинетическая энергия твердого тела при его плоском движении равна сумме кинетической энергии тела в поступательном движении вместе с центром масс и кинетической энергии во вращении тела вокруг подвижной оси (3.64). На основе теоремы Кенига имеем:
,
Рис. 3.63 Рис. 3.64
где
- кинетическая энергия тела в поступательном
движении вместе с центром масс;
- кинетическая энергия во вращении
тела вокруг подвижной оси Сz.
10.2. Теорема об изменении кинетической энергии материальной точки
Дифференциальная форма. Дифференциал от кинетической энергии материальной точки равен элементарной работе силы, действующей на точку,
.
Интегральная (конечная) форма. Теорема об изменении кинетической энергии материальной точки (рис. 3.65): изменение кинетической энергии материальной точки на некотором ее перемещении равно алгебраической сумме работ всех действующих на эту точку сил на том же перемещении.
Рис. 3.65
10.3. Кинетическая энергия механической системы
Кинетическая энергия механической системы определяется как сумма значений кинетической энергии всех входящих в эту систему материальных точек.
.
По теореме С.Кенига кинетическая энергия механической системы равна сумме кинетической энергии центра масс системы, масса которого равна массе всей системы, и кинетической энергии этой системы в ее относительном движении относительно центра масс.
,
где
- скорость центра масс системы;
-
относительная скорость точки системы
в ее движении относительно центра масс.
10.4. Теорема об изменении кинетической энергии механической системы
Теорема об изменении кинетической энергии механической системы формулируется: изменение кинетической энергии механической системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних cuл, приложенных к системе, на этом перемещении (рис. 3.66). Таким образом,
Рис. 3.66
.
В
случае неизменяемой системы сумма
работ внутренних сил на любом перемещении
равна нулю (
),
тогда
,
т. е. изменение кинетической энергии твердого тела при любом перемещении равно сумме работ всех действующих на тело внешних сил на этом перемещении.
10.5. Потенциальное силовое поле и потенциальная энергия
Силовым полем называется пространство, в котором на точки механической системы действуют силы, зависящие от положения этих точек и времени нахождения в этом поле. Силовое поле называется потенциальным, если оно обладает свойствами: силы поля зависят лишь от координат точки поля и силы поля консервативны. Силы называются консервативными, если работа этих сил не зависит от способа осуществления перемещения и определяется лишь начальными и конечными положениями системы.
Полная работа консервативных сил на каком-либо перемещении точки ее приложения равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории, по которой оно совершается:
где функция U от координат х, у, z, полный дифференциал которой равен элементарной работе, называется силовой функцией.
На ряду с силовой функцией для потенциального силового поля вводится другая функция, характеризующая запас энергии, которой обладает точка в заданном положении.
Потенциальной энергией П материальной точки в заданной точке М потенциального силового поля называется работа, которую совершают силы поля, действующие на материальную точку при перемещении ее из точки М в начальную точку М0.
Проекции
на координатные оси силы, действующей
в потенциальном поле на каждую точку
механической системы, равны взятым со
знаком минус частным производным от
потенциальной энергии системы по
соответствующим координатам этой точки.
Поле силы тяжести. Потенциальная энергия механической системы, находящейся под действием сил тяжести, равна произведению веса системы на высоту ее центра тяжести (рис. 3.67).
Рис. 3.67
,
где
.
Поле силы упругости. Потенциальная энергия точки при действии силы упругости определяется по зависимости
.
Закон сохранения механической энергии. При движении механической системы под действием сил, имеющих потенциал, изменения кинетической энергии системы определяются зависимостями:
,
откуда
,
т.е.
.
Сумму кинетической и потенциальной энергий системы называют полной механической энергией системы.
Таким образом, при движении механической системы в стационарном потенциальном поле полная механическая энергия системы при движении остается неизменной.
Задача 3.17. Груз А веса Р, опускаясь по наклонной плоскости вниз со скоростью v, приводит во вращение барабан В веса Q посредством намотанной на него веревки. Барабан считать однородным круглым цилиндром. Массой веревки пренебречь. Вычислить кинетическую энергию системы, выразив ее через скорость груза А (рис. 3.68).
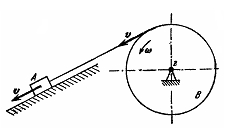
Рис. 3.68
Решение.
Система состоит из двух масс груза А
и барабана В.
Следовательно, кинетическая энергия
системы равна сумме кинетических энергий
груза
и барабана
.
(а)
Кинетическая энергия груза, движущегося поступательно, вычисляется по формуле
.
(б)
Кинетическая энергия барабана, вращающегося вокруг неподвижной оси z, перпендикулярной к плоскости рисунка, находится по формуле
,
(в)
где
- момент инерции барабана относительно
оси вращения z; 
- угловая скорость вращения барабана.
Барабан сплошной однородный цилиндр
,
(г)
где
r
- радиус
барабана. Подставив значение
из формулы (г) в формулу (в), имеем:
.
Учитывая,
что скорость точки на ободе барабана
равна скорости груза, получим:
и, следовательно,
.
(д)
После
подстановки значений
и
из формул (б) и (д) в (а) находим искомую
кинетическую энергию системы
.
Задача
3.18. Груз
весом Р,
лежащий посередине упругой балки,
совершает свободные колебания. Упругая
сила балки пропорциональна ее прогибу
и направлена по вертикали. Проекция
упругой силы на вертикальную ось
х равна
,
где
- прогиб балки в ее середине, а с
- коэффициент упругости, численно равный
силе, которую надо приложить в середине
балки для того, чтобы прогнуть ее на
единицу длины (рис. 3.69). Вычислить
потенциальную энергию системы, пренебрегая
массой балки.
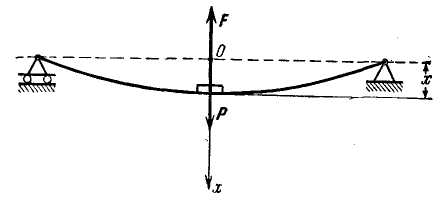
Рис. 3.69
Решение.
Возьмем начало отсчета оси х
в середине недеформированной балки.
Изобразим силы, приложенные к грузу:
- вес груза,
-упругая сила балки. Обе силы
потенциальны. Для вычисления потенциальной
энергии груза надо сложить потенциальные
энергии силы тяжести
и упругой силы
.
(а)
Так как потенциальной энергией называется работа потенциальной силы при перемещении материальной точки из данного положения в нулевое, то
.
(б)
Потенциальная энергия силы тяжести отрицательна при х > 0, так как груз для перемещения из данного положения в нулевое должен подняться вверх. Далее находим
.
(в)
Потенциальная энергия упругой балки положительна. Подставив формулы (б) и (в) в (а), находим искомое выражение потенциальной энергии системы:
.
Задача 3.19. Механическая система под действием сил тяжести приходит в движение из состояния покоя. Учитывая трение скольжения тела 3, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость и ускорение тела 1 в тот момент, когда пройденный им путь станет равным s (рис. 3.70). В задаче принять:
Решение.
На механическую систему действуют
активные силы
,
,
.
Применяя принцип освобождения от связей
системы, покажем реакции шарнирно-неподвижной
опоры 2 и шераховатой наклонной
поверхности. Направления скоростей тел
системы изобразим с учетом того, что
тело 1 спускается (рис. 3.70,б).
Задачу решим, применяя теорему об изменении кинетической энергии механической системы:
,
где
Т
и
– кинетическая энергия системы в
начальном и конечном положениях;
-
алгебраическая сумма работ внешних
сил, приложенных к системе, на перемещении
системы из начального положения в
конечное;
-
сумма работ внутренних сил системы на
том же перемещении.
Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями,
.
Так
как в начальном положении система
покоилась, то
.
Следовательно,
.
а)
б)
Рис. 3.70
Кинетическая энергия системы представляет собой сумму кинетических энергий тел 1, 2, 3
.
Кинетическая энергия груза 1, движущегося поступательно, равна:
.
Кинетическая энергия блока 2, совершающего вращение вокруг оси Оz, перпендикулярной плоскости чертежа,
.
Кинетическая энергия тела 3 в его поступательном движении
.
Таким образом,
.
Выражение
кинетической энергии содержит неизвестные
скорости всех тел системы. Начать
определение необходимо с
.
Избавимся от лишних неизвестных, составив
уравнения связей.
Уравнения связей это не что иное, как кинематические соотношения между скоростями и перемещениями точек системы. При составлении уравнений связей выразим все неизвестные скорости и перемещения тел системы через скорость и перемещение груза 1.
Скорость
любой точки обода малого радиуса
равна скорости тела 1, а также произведению
угловой скорости тела 2 и радиуса вращения
r
.
Отсюда выразим угловую скорость тела 2
.
(а)
Вращательная
скорость любой точки обода блока большого
радиуса
,
с одной стороны, равна произведению
угловой скорости блока и радиуса
вращения, а с другой – скорости тела 3
.
Подставив значение угловой скорости, получим:
.
(б)
Проинтегрировав при начальных условиях выражения (а) и (б), запишем соотношение перемещений точек системы:
.
(в)
Зная основные зависимости скоростей точек системы, вернемся к выражению кинетической энергии и подставим в него уравнения (а) и (б):
.
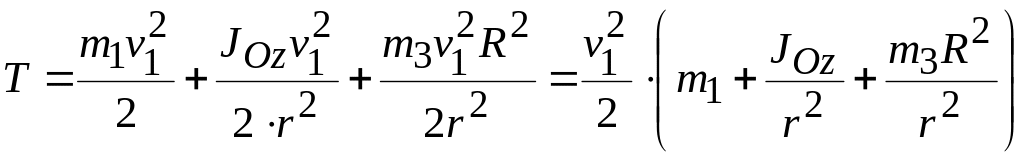Момент инерции тела 2 равен:
.
Подставляя значения масс тел и момента инерции тела 2, запишем
.
Определение суммы работ всех внешних сил системы на заданном перемещении.
.
Работа силы тяжести тела 1
.
Работа
сил
равна нулю, так как эти силы приложены
к неподвижной точке.
.
Работа силы тяжести тела 3
.
Работа нормальной реакции тела 3 равна нулю, так как сила перпендикулярна направлению движения
.
Работа силы трения скольжения
,
так как
,
тогда
.
Сумма работ внешних сил
.
Подставляя значения масс тел, соотношения перемещений (в) и числовые параметры, запишем:
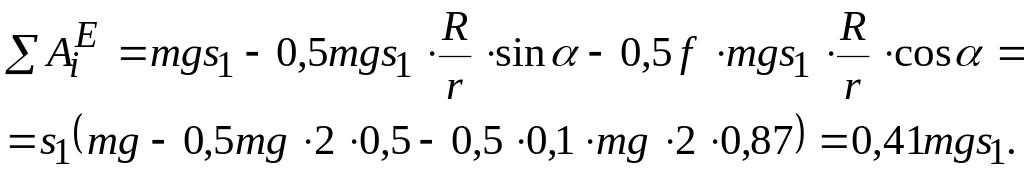
Теперь согласно теореме об изменении кинетической энергии механической системы приравняем значения Т и
.
(г)
Скорость тела 1 получим из выражения (г)
.
Ускорение тела 1 можно определить, продифференцировав по времени равенство (г):
,
где
.
Тогда
.