Глава 12. Принцип возможных перемещений

12.1. Принцип возможных перемещений

Возможными (или виртуальными) перемещениями точек ме­ханической системы называются воображаемые бесконечно малые пере­мещения, которые допускают наложенные на систему связи.

Принцип возможных перемещений, формулируется так: необходимым и достаточным условием равновесия системы сил, приложенных к меха­нической системе, подчиненной стационарным двусторонним и идеаль­ным связям, заключается в равенстве нулю суммы элементарных работ задаваемых сил на любом возможном перемещении системы из рассматриваемого ее положения.

.

Принцип возможных мощностей: при равновесии механической системы под действием активных сил сумма возможных мощностей этих сил равна нулю.

Задача 3.21. Определить с помощью принципа возможных перемещений реакции опор составной конструкции (рис. 3.75).

Рис. 3.75

Решение. Определение .Заданная составная балка под действием плоской произвольной системы сил находится в равновесии, т.е. не имеет ни одной степени свободы. Для определения зададим одну степень свободы, соответствующую этой реакции, заменив шарнирно-неподвижную опору А шарнирно-подвижной, приложив в точке А .

В результате составная балка получила возможность поступательного движения вдоль горизонтали. Покажем возможное перемещении балки таким образом, чтобы реакция ему препятствовала (рис. 3.76).

Рис. 3.76

Для равновесия механической системы с двухсторонними идеальными связями необходимо и достаточно, чтобы сумма элементарных работ задаваемых сил на любом ее возможном перемещении была равна нулю

.

Уравнение возможных работ:

.

Данное выражение содержит неизвестную реакцию , которую условно причислили к задаваемым силам, и неизвестные возможные перемещения точек приложения сил и . Так как вся система совершает поступательное движение, то возможные перемещения точек приложения сил равны:

;

.

Определение реакции

.

Определение . Для определения следующей реакции вернемся к исходной схеме и повторим ход решения сначала. Дадим возможное перемещение балки в точке А вдоль направления реакции , заменив шарнирно-неподвижную связь шарнирно-подвижной и показав . Так как в точке В балка перемещаться вертикально не может, то левая часть составной конструкции повернется на некоторый угол вокруг точки В, например, против хода часовой стрелки (рис. 3.77). Шарнир С вместе с левой частью переместится на , заставив правую часть конструкции балки СD повернуться на угол вокруг точки D. Так как углы поворота очень малы, то считаем, что никаких горизонтальных перемещений точек балки нет. Уравнение возможных работ запишем с учетом того, что работа силы при повороте тела равна произведению момента силы относительно центра вращения на угол поворота тела:

.

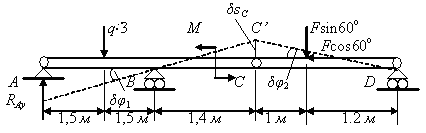
Рис. 3.77

Свяжем углы поворота и с помощью перемещения шарнира С . Рассмотрим треугольник СВС’, в котором СС’= :

.

Так как очень мал, то или

.

Из треугольника DCC’ следует

,

т.е. . Подставляя значения отрезков ВС и CD, запишем

,

откуда

.

Подставляем значение в уравнение возможных работ и делим левую и правую части этого выражения на :

;

.

Теперь определим неизвестную реакцию

кН.

Для определения реакции дадим возможное перемещение балки в точке В вдоль направления реакции, т.е. вдоль вертикали. Так как в точке А вертикальное перемещение невозможно, то балка АС повернется вокруг этой точки на угол , часть CD составной конструкции повернется вокруг точки D на угол (рис. 3.78).

Рис. 3.78

Уравнение возможных работ

.

Свяжем возможные перемещения отдельных частей конструкции с помощью шарнира С

,

откуда

.

Подставив значение в уравнение возможных работ

и сократив его на неизвестное возможное перемещение, получим:

,

Откуда

кН.

Последнюю реакцию определим, задав возможное перемещение балки в точке D вдоль вертикали. Балка АС остается неподвижной, а часть CD повернется вокруг точки на угол (рис. 3.79).

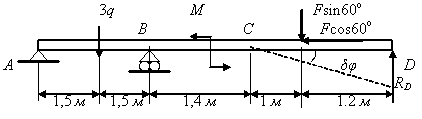
Рис. 3.79

Уравнение возможных работ (рис. 3.80)

или

,

откуда

кН.

Правильность решения можно проверить, записав уравнения статики:

.

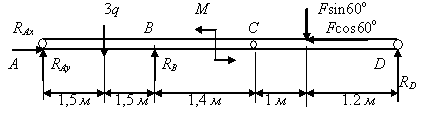
Рис. 3.80

Подставив найденные значения реакций в уравнения проверки, получим:

.

Знаки плюс в ответах означают, что предположительные направления реакций оказались верными.

  Задача 3.22.  Через блок А весом Р переброшен канат, к концам которого привязаны груз В и каток С весом , лежащий на идеально гладкой наклонной плоскости. Через каток С, в свою очередь переброшен канат, к концам которого привязаны груз D весом и груз Е весом , лежащий на параллельной идеально гладкой плоскости. Определить вес груза В и угол  α, образуемый наклонными плоскостями с горизонтом, если система находится в равновесии. Весом канатов пренебречь (рис. 3.81).

Решение. Рассматриваемая система имеет две степени свободы, так как для определения положения всех ее точек надо задать два независимых параметра. Один параметр должен определять положение груза В, а второй - положение грузов D и Е по отношению к катку С.

Изобразим задаваемые силы: - вес блока А, - вес груза Е, - вес груза D, - искомый вес груза В и - вес катка С. Силы реакций связей изображать не следует, так как все связи, наложенные на систему, являются идеальными (канаты натянуты и нерастяжимы, наклонные плоскости идеально гладкие).

Рис. 3.81

Дадим системе два независимых возможных перемещения (число независимых возможных перемещений равно числу степеней свободы системы):  δr_В - возможное перемещение груза В, направленное по вертикали вниз, и  δr_D  - возможное перемещение груза D, также направленное по вертикали вниз.

Применим принцип возможных перемещений для составления уравнений равновесия системы. Число уравнений должно быть равно числу ее степеней свободы. Поэтому для данной системы составим два уравнения равновесия.

Для составления уравнения равновесия системы, соответствующего возможному перемещению dr_D , будем считать возможное перемещение  δr_B  равным нулю, т.е.   ,   (это допустимо, так как возможные перемещения  и   являются независимыми). При этом груз В и каток С останутся в покое, груз D переместится на   по вертикали вниз, а груз Е переместится на  параллельно наклонной плоскости вверх. Применив принцип возможных перемещений, получим:

,

откуда

.  (а)

Для составления уравнения равновесия системы, соответствующего возможному перемещению   , будем считать возможное перемещение  равным нулю, т.е. ,   . При этом грузы D и Е по отношению к катку С останутся в покое, груз В переместится на   параллельно наклонной плоскости вверх. Применив принцип возможных перемещений, имеем:

,

откуда

. (б)

Подставив в формулу (б) значение из формулы (а), найдем искомую величину веса груза В:

.

Задача 3.23. Применяя принцип возможных перемещений и пренебрегая силами сопротивления, определить величину силы , которую необходимо приложить, чтобы удержать механизм в равновесии (рис. 3.82).

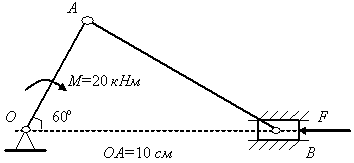
Рис. 3.82

Решение. Рассматриваемый механизм находится в равновесии под действием пары сил с моментом М и сосредоточенной силы .

Связи, наложенные на механическую систему, допускают возможные перемещения звеньев механизма: поворот кривошипа ОА вокруг оси проходит через точку О, поступательное движение ползуна В и плоское движение шатуна АВ. В целом система имеет одну степень свободы, так как достаточно знать одну обобщенную координату, чтобы определить положение всех точек механизма. Зададим возможную угловую скорость кривошипа ОА , показав ее в сторону действия пары сил.

Шарнир А, вращаясь вместе с кривошипом, приобретет вращательную скорость , перпендикулярную радиусу вращения ОА и направленную в сторону .

Ползун В может перемещаться вдоль горизонтали ОВ. Проведем перпендикуляры в точках А и В к их возможным скоростям, в пересечении перпендикуляров (точка Р) будет находиться мгновенный центр скоростей.

Направление угловой скорости звена АВ должно соответствовать (рис. 3.83).

Запишем уравнение возможных мощностей, выражающие принцип возможных скоростей:

.

Уравнение содержит три неизвестных величины: . Избавимся от неизвестных скоростей, выразив через . Шарнир А участвует одновременно в двух движениях: совершает вместе с кривошипом ОА вращение вокруг оси, проходящей через точку О, и поворачивается вместе с шатуном АВ вокруг оси, проходящей через мгновенный центр скоростей. Скорость точки A в таком случае можно записать

,

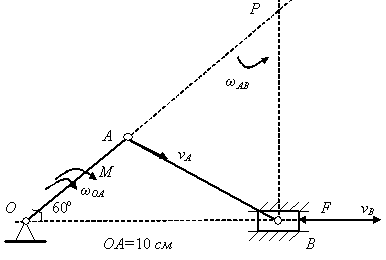
Рис. 3.83

откуда

.

Расстояние от точки А до мгновенного центра скоростей определим, рассмотрев два треугольника ОАВ и ВАР. Из Δ ОАВ найдем

.

Из Δ ВАР найдем

или ,

т.е.

.

Скорость точки В во вращении вместе со звеном АВ вокруг мгновенного центра скоростей запишем в виде

,

где

см;

.

Подставим теперь значение в уравнение возможных мощностей

или после сокращения на

.

Определение неизвестных параметров.

.