7.2. Вращение твердого тела вокруг неподвижной оси

Кинетический момент вращающегося твердого тела относительно неподвижной оси его вращения равен произведению момен­та инерции тела относительно той же оси на угловую скорость тела (рис. 3.42).

.

Рис. 3.42

Теорема об изме­нении кинетического момента механической системы выражается урав­нением

.

Так как

,

то

,

а потому уравнение принимает вид

. (3.19)

Уравнение (3.19) представляет собой дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.

Задача 3.14. Натяжения ветвей ремня, приводящего во вращение шкив, равны 20 и 40 Н. Шкив имеет вес 80 Н, радиус 30 см и радиус инерции относительно оси вращения 25 см. Составить уравнение вращения шкива из состояния покоя, пренебрегая трением (рис. 3.43).

Решение. Дифференциальное уравнение вращения шкива вокруг непод­вижной оси Ох имеет вид

.

К шкиву приложены внешние силы: реакции ветвей ремня и , вес шкива и составляющие реакции опоры и .

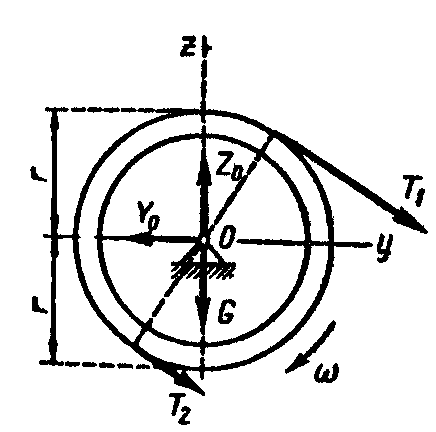
Рис. 3.43

Направление вращения тела принимают всегда за положительное. Тогда моменты сил, направленных в сторону вращения, положительны, а моменты сил, направленных противоположно, отрицательны. Главный момент внешних сил

(моменты сил , , относительно оси Ох равны нулю). Момент инерции шкива определяем по радиусу инерции:

.

Подставляем числовые значения и в уравнение

Отсюда находим угловое ускорение

.

Интегрируем дважды по t:

.

По начальным условиям находим С₁ = 0 и C₂=0. Таким образом, уравнение вращения шкива имеет вид

.

7.3. Плоское движение твердого тела

Дифференциальные уравнения плоского движения твердого тела представляют собой совокупность уравнений поступательного движения плоской фигуры вместе с центром масс и вращательного движения относительно оси, проходящей через центр масс (рис. 3.44).

.

В том случае, когда траектория центра масс задана, удобно поль­зоваться дифференциальными уравнениями движения точки С в проек­циях на касательную и главную нормаль к этой траектории.

Тогда дифференциальные уравнения плоского движения твердого тела имеют вид:

.

Рис. 3.44

где s_c - дуговая координата центра масс, v_c - его скорость и ρ - радиус кривизны его траектории.

Задача 3.15. Однородный цилиндр весом G и радиусом r катится без скольжения по наклонной плоскости, составляющей с горизонтом угол а. Коэффициент сцепления равен (рис. 3.45). Определить ускорение движения центра масс цилиндра и угол наклона плоскости, при котором начинается скольжение цилиндра, без учета сопротивления качению.

Решение. Движение цилиндра совершается под действием трех внешних сил: силы тяжести , нормальной реакции плоскости и силы сцепления . Направим оси х и у, как указано на рисунке. Через центр масс цилиндра С проведем оси ξ и η и ось ζ, перпендикулярную плоскости чертежа. Момент силы относительно оси Сζ будет положителен, если сила стремится вращать плоскость чертежа вокруг точки С в направлении против вращения часовой стрелки, и отрицателен - в противоположном случае.

Рис. 3.45

Составим дифференциальные уравнения плоского движения тела:

, (а)

, (б)

. (в)

Так как за рассматриваемый промежуток времени у_с = r = const, то , а потому из уравнения (б)

, откуда .

Дифференциальные уравнения (а) и (в) содержат три неизвестные вели­чины: и . Для определения этих неизвестных к двум составленным уравнениям добавим еще одно.

Так как цилиндр катится без скольжения, то точка Р соприкасания среднего сечения цилиндра с плоскостью является мгновенным центром скоростей среднего сечения. Поэтому

. (г)

Проекция скорости точки С на ось х

.

Алгебраическая величина угловой ско­рости отрицательна, так как цилиндр вращается по вращению часовой стрелки, т. е.

,

где |ω| — абсолютное значение угловой ско­рости.