§28 Теорема Штурма(отделение действительных корней многочлена)
Пусть дан многочлен n степени с действительными коэффициентами (1)
По основной теореме алгебры многочлен имеет ровно n корней если многочлен имеет комплексные корни то они встречаются парами как комплексные сопряжённые. Комплексных корней всегда четное число, по этому число действительных корней с учетом кратности либо равно степени многочлена либо на четное число меньше, в частности любой многочлен не четной степени имеет худобы 1 действительный корень.
Представляет интерес определения
точного числа действительных корней
многочлена а также промежутков их
принадлежности. Можно показать, что все
действительные корни многочлена
принадлежат интервалу 
Ответить на вопрос сколько многочлен имеет действительных корней в заданном интервале позволяет теорема штурма, в которой используются функции штурма.
Для построения ряда штурма выполняют следующую процедуру: находят производную многочлена как функции f(x) это будет некоторый многочлен с действительными коэффициентами. Для многочленов f(x) и f`(x) выполняют алгоритм похожий на алгоритм Евклида:
Если данный многочлен не имеет кратных
корней то в этом случае 
то последний остаток является многочленом
нулевой степени то есть числом.
Последовательность многочленов:
называется ряд функций штурма. В
дальнейшем нас будут интерисовать знаки
тех значений которые принимают функции
ряда штурма по этому функции образующее
последовательность (2) можно находить
с точностью до постоянного положительного
множителя.
Т(Штурма): Если a,b
и не являются корнями многочлена
f(x)не
имеющего кратных корней то число
действительных корней этого многочлена
принадлежащих интервалу (a,b),
где s(x)
количество перемен знаков в ряде
функций штурма соответственно в точках
a,b.
§29 Отыскание рациональных корней многочлена
Т1: Если рациональное число 
является корнем многочлена f(x)
то свободный член делится на p
а старший коэффициент делится на q.
Доказательство:
по
условию. Обе части этого выражения
умножим на 
/…СБ4/
2 часть доказательства
Левая часть делится на q
.
Если старший член равен 1 (нормированный) то все рациональные корни этого многочлена являются целыми числами причем делителями свободного член
,
,
,
cследовательно корень
целый.
Т2: Если рациональное число
где p,q
взаимно простые является
корнем многочлена f(x)
то для любого целого числа k:
применима теорему о делении 
Доказательство:
Если предположить, что (
Получаем, что наша дробь сократима, что
противоречит нашему условию. Мы пришли
к тому, что 
делится не может следовательно 
■
Следствие: Если многочлен с целыми
коэффициентами нормированный то его
рациональными корнями могут быть только
такие целые числа для которых при любом
Доказательство:
По Т2 
30 Т(Критерий не приводимости Эйзенштейна):
Если в многочлене с целыми коэффициентами
f(x) коэффициенты
все до старшего делятся на некоторое
простое число p и старший
коэффициент не делится на p
причем 
,
то такой многочлен не приводим над
полем рациональных чисел Q.
Доказательство:
Пусть эти требования выполняются но многочлен является приводимым то есть представляется в виде произведения:
пусть
Подставим выражения для 
в равенство(2).
Выполним почвенное умножение в правой части равенства, приведем подобные слагаемые и воспользуемся определением равных многочленов то есть мы приравняем соответствующие коэффициенты:
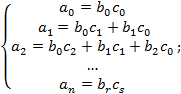
По условию теоремы 
Учитывая, что 
,
то 
,
тогда либо
или либо 
.
По условию 
.
Продолжая так и далее получим, что 
от куда следует, что 
,
что противоречит условию, что и доказывает
нашу теорему. Заметим, что рассматривая
второй случай также пришли к противоречию.
В этом случае было бы получено, что
что значит и 
что противоречит теореме.
■
Замечание: Из теоремы следует
существование многочленов сколь угодно
большой степени с целыми коэффициентами
не приводимыми над полем Q.
Например 
является не приводимым над Q.
Пример 1:
Доказать не приводимость многочленов пользуясь критерием Эйзенштейна:
На полем Q не приводим.
Алгебраические числа.