§25 Решение кубических уравнений

Пусть дано уравнение 3 степени. нормируя получим (1) применим подстановку:

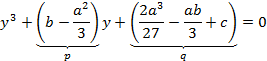
Пусть :

Если система имеет решение то сумма эти чисел равно которое будет решением уравнения (2) а потом и данного уравнения. Перепишем систему (3):

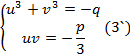
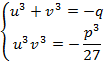
Считая некоторыми корнями квадратного уровнения составим его с помощи теоремы Виета.

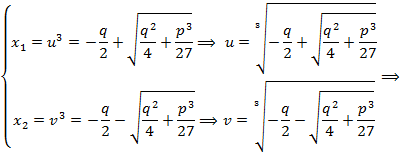
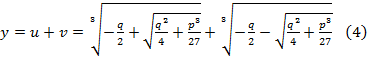
Так как кубическое уравнение имеет 3 решения то для u и v найдется по 3 решения, а их сумма дает 9 вариантов корней в действительности они должны быть выбраны, что бы выполнялись условия системы (3`) то есть .

Докажем что корней 3. Воспользуемся теоремой из комплексных чисел:

26

Т1: Что бы извлечь корень энной степени из комплексного числа z достаточно какое-нибудь 1 значение корня умножить последовательно на корни энной степени из 1 тоесть

также являются корнями.

Извлекаем корень из 1

Пусть какой-то значения кубических корней:

и

Тогда другими значения первого кубического корня будут

Заметим, что значению отвечает значение

Значению отвечает значение

Корнями уравнения (2) будут:

■

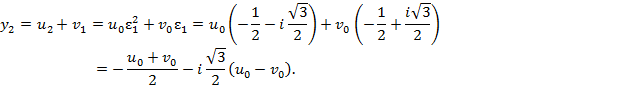
Решения приведенного кубического уравнения (2) находят по формулам:

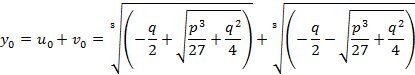
Где выражения дискриминант.

Пример 1:

Т2: Если дискриминант кубического уравнения равен 0 то уравнение имеет 2 равных корня.

Доказательство:

Пусть одно из значений получается при тогда найдем соответствующее значение из условия:

■

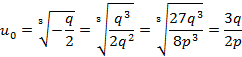
Т3: Пусть кубическое уравнение имеет действительные коэффициенты:

1. Если D>0 то уравнение имеет 3 различных корня причем 1 действительный и 2 комплексных сопряжённых.

2. Если дискриминант меньше 0 то уравнение имеет три различных действительных корня.

3. Если декремента равен 0 то три действительных корня 2 из которых равны между собой.

Доказательство:

1. Пусть D>0 тогда 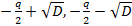два действительных числа, тогда получаем 1 корня действительных, а 2 мнимых, обозначим:

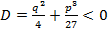2. тогда получим 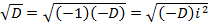тогда мнимые. И все корни кубические из этих чисел также будут мнимыми. Все корни мнимые причем все эти корни имеют один и тот же модуль. 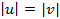. Покажем, что мнимые: ,u-0.,v-0.=-,p-3.>0(т.к дескрименант меньше 0). Таким образом, равенство модулей и положительное действительное число произведение, возможно только для комплексных сопряжённых

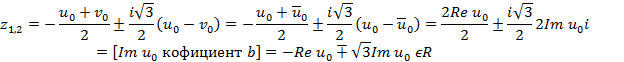
3. В Т1 было показано, что ,u-0.=,3q-2p. ,v-0.=,3q-2p. и корни ,z-0.=,3q-p. ,z-1,2.=-,3q-2p.

■

§27 Решение уравнений 4 степени(Феррари)

Пусть дано нормированное уравнение 4 степени ,x-4.+a,x-3.+b,x-2.+cx+d=0

Все слагаемые начиная с 2 переносим в право ,x-4.+a,x-3.=-b,x-2.-cx-d

,,,x-2..-2.+,2a-2.,x-2.x+,,a-2.-4.,x-2.=,,a-2.-4.,x-2.-b,x-2.-cx-d

,,,x-2.+,a-2.x.-2.=,,,x-2.-4.-b.,x-2.-cx-d

Введём вспомогательную переменную t что бы левая и правая имели полные квадраты

,,,,x-2.+,a-2.x.+,t-2..-2.=,,,a-2.-4.-b.,x-2.-cx-d+,2t-2.,,x-2.+,a-2.x.+,,t-2.-4.

,,,,x-2.+,a-2.x.+,t-2..-2.=,,,a-2.-4.-b+t.,x-2.+,,at-2.-c.x+,,,t-2.-4.-d.

Чтобы правая часть была полным квадратом необходимо чтобы дискрименат был равен 0

D=,,,at-2.-c.-2.-4,,,a-2.-4.-b+t.,,,t-2.-4.-d.=,,a-2.,t-2.-4.-,2at-2.c+,c-2.-,,a-2.,t-2.-4.+b,t-2.-,t-3.+,a-2.d--abd+4td

,t-3.-b,t-2.+,ac-4d.t+4bd-,c-2.-,a-2.d=0-кубическая резальента уровнения 4 степени

Находим 1 из корней кубической резольвенты и подставляем его:

,,,x-2.+,a-2.x+,,t-0.-2..-2.=,,Ax+B.-2.

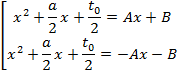
Существуют и другие например способ Эйлера Декарта.

Пример1:

,x-4.-2,x-3.+2,x-2.+4x-8=0

,,,x-2..-2.-2,x-2.x+,x-2.=-,x-2.-4x+8

,,,x-2.-x.-2.=-,x-2.-4x+8

,,,x-2.-x+,t-2..-2.=-,x-2.-4x+8+,2t-2.,,x-2.-x.+,,t-2.-4.

,,,x-2.-x+,t-2..-2.=,t-1.,x-2.-,t+4.x+,8,t-2.-4.

D=,,t+4.-2.-4,t-1.,8+,,t-2.-4..=,t-2.+8t+16-32t+32-,t-3.+,t-2.=-,t-3.+2,t-2.-24t+48

,t-3.-2,t-2.+24t-48=0

,t-0.=2

,(x-2.-x+1)^2=x^2-6x+9

,,,x-2.-x+1.-2.=,,x-3.-2.

,,,x-2.-x+1=x-3,-,x-2.-x+1=3-x..

Замечание: Начиная с 16 века почти 3 лет продолжались попытки ученых разрешить уравнения 5 степени и выше в радикалах (выразить корни уравнений в виде выражений содержащих коэффициенты). В 19 веке была доказана теорема Руфини Абеля о том, что алгебраическое уравнение n степени с произвольными буквенными коэффициентам при n>=5 нельзя решить в радикалах.