
- •Л1 02.09.09 Алгебра многочленов
- •§1: Многочлены как функции действительной переменной
- •§2 Алгебраическое определение кольца многочленов
- •§3 Кольцо многочленов над областью целостности
- •§4 Деление с остатком многочлена на двучлен (X- )
- •§5 Наибольшее возможное число корней в области целостности.
- •§6 Деление с остатком
- •§ 7 Наибольший общий делитель многочленов. Алгоритм Евклида.
- •§ 8 Наименьшее общее кратное двух многочленов.
- •§9 Многочлены не приводимые над полем
- •§10 Разложение многочлена в произведении нормированных не приводимых множителей
- •§11 Формальная производная многочлена
- •§12 Не приводимые кратные множители многочлена.
- •§ 13 Кратные корни многочлена
- •§14 Разложение многочлена по степеням двучлена
- •§15 Кольцо многочленов от n переменных
- •§16 Степень многочлена. Лексикографическое упорядочение членов многочлена.
- •§17 Разложение многочлена от n переменных в произведение не приводимых множителей
- •§18 Cсимметрические многочлены
- •§ 19 Основная теорема о симметрических многочленах.
- •§20 (Дополнение к теме нод). Результант 2 многочленов
- •§21 Многочлены над полем комплексных чисел
- •§ 22 Зависимость между корнями. Теорема Виета.
- •§23 Свойства мнимых корней многочлена с действительными коэффициентами
- •§24 Разложение многочлена над полем действительных чисел в произведение не приводимых множителей
- •§25 Решение кубических уравнений
- •§27 Решение уравнений 4 степени(Феррари)
- •§28 Теорема Штурма(отделение действительных корней многочлена)
- •§29 Отыскание рациональных корней многочлена
- •30 Т(Критерий не приводимости Эйзенштейна):
- •31 Простое алгебраическое расширение как линейное пространство.
- •32 Избавление от иррациональности
Л1 02.09.09 Алгебра многочленов
Лит: Винбег Алгебра многочленов
Задачник практикум
Т1: Многочлены от одной переменной
§1: Многочлены как функции действительной переменной
Рассмотри понятия многочлена или целой рациональной функции от одной переменной.
О1) функция вида:
![]() (1) –называется многочленом
(1) –называется многочленом
Где
![]() действительные числа, x
действительная переменная, n
целое число- степень многочлена.
действительные числа, x
действительная переменная, n
целое число- степень многочлена.
коэффициенты,
Число n называют
степенью многочлена, ![]() – свободный член.
– свободный член.
С точке зрения мат записи имеем сумму например:
![]() - 1 степени;
- 1 степени;
![]() -2 степени;
-2 степени;
Частным случаем является постоянная функция f(x)=a ,a-cost.
Многочлен коэффициенты которого равны 0 называется, многочлен нулевой степени.
Заметим что над многочленами можно
выполнять: сложение, вычитание, умножения
в результате чего получается снова
многочлен. Пусть имеется многочлен (1)
и многочлен:
![]() ;(2)
;(2)
тогда:
![]() ;
;
Произведением многочленов f и g называется сумме всевозможных произведений U*V где U любой член из f(x), а V из g(x) тогда:
![]() ;
;
где:
![]()
Так как сумма, разность и произведение многочленов также являются многочленом то многочлены образуют под кольцо в кольце всех функций действительного аргумента. Кольцо многочленов от действительной переменной x обозначается R[x] . Поскольку кольцо всех функций коммутативно и ассоциативно кольцо R[x] также обладает этими свойствами а значит в нем существует единичный элемент f(x)=1. Многочлены в алгебре также в связи с решением уравнений f(x)=0 где левая часть многочлен n-ной степени от одной переменной то в этом случае многочлен рассматривается как многочлен комплексной переменно. В алгебре рассматривают многочлены на более общих алгебраических системах, коэффициенты которых принадлежат произвольному кольцу, значительно отличаются от многочленов с числовыми коэффициентами.
§2 Алгебраическое определение кольца многочленов
О1) Пусть R[x] произвольное кольцо многочленов от переменной х с коэффициентами из R назовем формальное выражение:
![]() (1)
(1)
где n целое число
выражение (1)
надо рассматривать как единый символ
у которого операции над отдельными
частями не подразумевается
![]() будем называть коэффициентами многочлена
(1)
при
будем называть коэффициентами многочлена
(1)
при
![]() ,
а для всех k>n
коэффициент при
равен 0 для обозначения многочлена
используют
,
а для всех k>n
коэффициент при
равен 0 для обозначения многочлена
используют
![]() .
.
Два многочлена будем считать равными
если каждый коэффициент
![]() из
из![]() равен
соответствующему коэффициенту
равен
соответствующему коэффициенту
![]() из
из
![]() и
записывается f(x)=g(x).
и
записывается f(x)=g(x).
Для многочленов (1) и(2) определим их сумму f(x)+g(x) и произведение f(x)*g(x) по формулам рассмотренным в §1. Эти определения согласуются с данным выше определением равенства многочленов:
f1(x)=f2(x);
g1(x)=g2(x);
f1(x)+g1(x)=f2(x)+g2(x);
f1(x)*g1(x)=f2(x)*g2(x);
Свойства умножения и сложения многочленов
коммутативность сложения путь f,g заданы (1) и(2) тогда согласно определения операции сложения будим иметь:
![]()
![]()
так как коэффициенты многочлена это
элементы кольца R то,
![]() ,
а следовательно мы получим g(x)+f(x)=
f(x)+g(x)
,
а следовательно мы получим g(x)+f(x)=
f(x)+g(x)
ассоциативность сложения
![]()
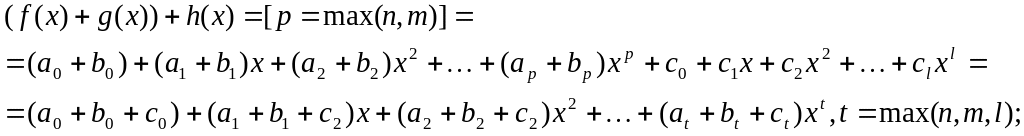
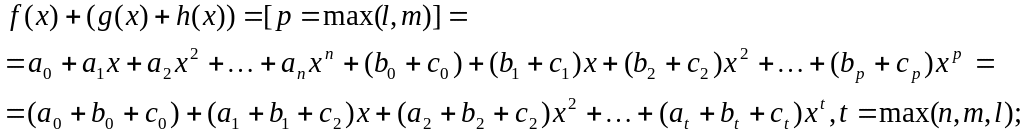
доказывается аналогично сделать дома
существование нуля. Назовем нулевым многочленом такой у которого коэффициенты равны 0 и обозначим символом 0. этот многочлен играет роль нейтрального элемента по сложению f(x)+0=f(x)
существование противоположного элемента –f(x) его коэффициенты противоположны соответствующим коэффициентам f(x), f(x)+(-f(x))=0
дистрибутивность умножения относительно сложения
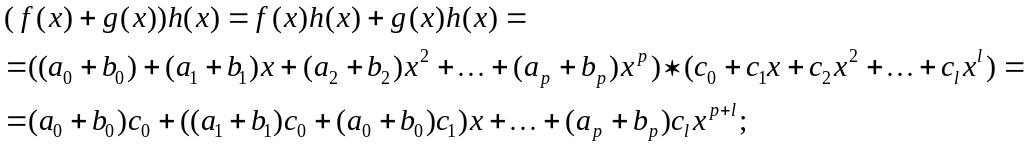
![]()
![]()
![]()
ассоциативность умножения

доказать самостоятельно
Свойства 1-6 означают что множество многочленов коэффициентами из кольца R образует кольцо относительно операций сложения и умножения многочленов.
Как и во всяком кольце в кольце многочленов можно определить операцию их вычитания.
![]()
Кольцо R является под
кольцом кольца многочленов ![]()
Предположим что в кольце R содержит единицу
![]()
По формуле произведения многочленов можно найти квадрат этого многочлена, куб и в общем случае:
![]()
умножая в поле многочленов элемент:
![]()
и выбрав ![]() мы можем утверждать, что
мы можем утверждать, что ![]() .
.
Путем сложения таких слагаемых получим
![]()
Коэффициенты этого многочлена![]() R-под
кольцо.
R-под
кольцо.
Введем понятие степени многочлена
Степенью не нулевого многочлена f(x)
называется наибольшее из таких чисел
n, что ![]() (сстепень
нулевого многочлена считается равной
мину бесконечности) и обозначается ст
f(x) всякий
многочлен степени большей или равной
0 будет записан в виде (1) где
(сстепень
нулевого многочлена считается равной
мину бесконечности) и обозначается ст
f(x) всякий
многочлен степени большей или равной
0 будет записан в виде (1) где ![]() .
При этом
.
При этом ![]() – называют старшим членом многочлена
(1).
– называют старшим членом многочлена
(1).
Если старший член равен 1 то он называется нормированный(приведённый) многочлен.
Рассматривая формулы по которым
определяются сумма многочленов мы
видим, что полученный многочлен не
содержит члены степени которых выше
чем ![]()
А произведение не содержит члены степень которых выше m+n
![]()
![]()
Пример 1:
![]()
![]()
![]()

![]()
