
- •Л1 02.09.09 Алгебра многочленов
- •§1: Многочлены как функции действительной переменной
- •§2 Алгебраическое определение кольца многочленов
- •§3 Кольцо многочленов над областью целостности
- •§4 Деление с остатком многочлена на двучлен (X- )
- •§5 Наибольшее возможное число корней в области целостности.
- •§6 Деление с остатком
- •§ 7 Наибольший общий делитель многочленов. Алгоритм Евклида.
- •§ 8 Наименьшее общее кратное двух многочленов.
- •§9 Многочлены не приводимые над полем
- •§10 Разложение многочлена в произведении нормированных не приводимых множителей
- •§11 Формальная производная многочлена
- •§12 Не приводимые кратные множители многочлена.
- •§ 13 Кратные корни многочлена
- •§14 Разложение многочлена по степеням двучлена
- •§15 Кольцо многочленов от n переменных
- •§16 Степень многочлена. Лексикографическое упорядочение членов многочлена.
- •§17 Разложение многочлена от n переменных в произведение не приводимых множителей
- •§18 Cсимметрические многочлены
- •§ 19 Основная теорема о симметрических многочленах.
- •§20 (Дополнение к теме нод). Результант 2 многочленов
- •§21 Многочлены над полем комплексных чисел
- •§ 22 Зависимость между корнями. Теорема Виета.
- •§23 Свойства мнимых корней многочлена с действительными коэффициентами
- •§24 Разложение многочлена над полем действительных чисел в произведение не приводимых множителей
- •§25 Решение кубических уравнений
- •§27 Решение уравнений 4 степени(Феррари)
- •§28 Теорема Штурма(отделение действительных корней многочлена)
- •§29 Отыскание рациональных корней многочлена
- •30 Т(Критерий не приводимости Эйзенштейна):
- •31 Простое алгебраическое расширение как линейное пространство.
- •32 Избавление от иррациональности
§ 22 Зависимость между корнями. Теорема Виета.
Т: Если числа ![]() являются корнями многочлена
являются корнями многочлена![]() n степени
n степени
То справедливы следующие формулы называемые формулами Виета:
![]()
![]()
![]()
…
![]()
Доказательство:
По условию числа
являются корнями многочлена![]() n степени из кольца С[Z]
этот многочлен можно представить в виде
произведения линейных множителей:
n степени из кольца С[Z]
этот многочлен можно представить в виде
произведения линейных множителей: ![]() .
Раскроим скобки в правой части (рассмотрим
эту процедуру для многочлена 3 степени)
.
Раскроим скобки в правой части (рассмотрим
эту процедуру для многочлена 3 степени)
![]()
![]()
На основании определения равенства 2 многочленов приравниваем коэффициенты при одинаковых степенях:
![]()
![]()
![]()
![]()
Из последних равенств следует формулы Виета.
■
Замечание: Рассмотренные формулы Виета обобщают известные из школьного курса математики формулы Виета
Пример 1:
Составить нормированный многочлен наименьшей степени имеющий простой корень -1 и двукратный корень i.
![]()
![]()
![]()
![]()
![]()
![]()
§23 Свойства мнимых корней многочлена с действительными коэффициентами
Т1: Если число ![]() является корнем многочлена f(x)
с действительными корнями то и сопряжённое
число также является корнем многочлена
f(Z).
является корнем многочлена f(x)
с действительными корнями то и сопряжённое
число также является корнем многочлена
f(Z).
Доказательство:
Пусть ![]() воспользуемся свойствами комплексных
сопряжённых чисел:
воспользуемся свойствами комплексных
сопряжённых чисел:
Сумма сопряжённых равна сопряжённому суммы и произведение сопряжённых равно сопряжённому произведения:
![]()
![]()
![]()
![]()
![]()
Воспользовавшись свойствами ![]()
С учетом того, что коэффициенты многочлена
числа действительные, то есть представимые
в виде ![]()
![]()
![]()
Таким образом получили ![]() является корнем.
является корнем.
■
Т2: Если число ![]() k кратности, для многочлена
f(z), то и
сопряжённое ему число имеет k
кратность для этого же многочлена.
k кратности, для многочлена
f(z), то и
сопряжённое ему число имеет k
кратность для этого же многочлена.
Доказательство:
По условию k кратности, тогда значение многочлена будет равно 0:
![]() ,
но
,
но ![]()
Учитывая Т1 будем иметь ![]()
Так как f(z)
с действительными коэффициентами то и
![]()
также многочлены с действительными
коэффициентами. Докажем, что ![]() (методом от противного) предположив,
что
(методом от противного) предположив,
что ![]() , учитывая Т1
, учитывая Т1 ![]() это будет многочлен с действительными
коэффициентами→
это будет многочлен с действительными
коэффициентами→![]() что противоречит условию.
что противоречит условию.
■
§24 Разложение многочлена над полем действительных чисел в произведение не приводимых множителей
Т1: Всякий многочлен f(x)ϵ R[x] с действительными коэффициентами степени больше 2 приводим над полем R.
Доказательство:
По условию ![]() поосновной теореме алгебы многочлен
имеет корень в поле C,
обозначим его
поосновной теореме алгебы многочлен
имеет корень в поле C,
обозначим его![]() возможны:
возможны: ![]() .
.
По теореме Безу
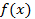 делится
на
делится
на 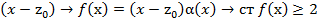 .
с
действительными коэфициентами и
.
с
действительными коэфициентами и 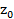 его корень. То есть
преводим над полем R.
его корень. То есть
преводим над полем R.Пусть
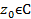 то сопряжённое ему также является
корнем. Следовательно по теореме Безу
данный многочлен будет делится на
то сопряжённое ему также является
корнем. Следовательно по теореме Безу
данный многочлен будет делится на 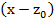 и
и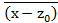 и делится на их произведение, а тогда
и делится на их произведение, а тогда
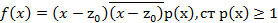
Рассмотрим ![]()
Многочлен с действительными коэффициентами представим в виде квадратного двучлена и многочлена p также с действительными переменными, то есть приводим над R.
■
Следствие: Над полем R не приводимы многочлены 1 степени и многочлены 2 степени которые имеют комплексные корни.
Т2: Всякий многочлен степени не ниже
1, единственным образом разлагается с
точностью до порядка множителей над
полем R в произведение
нормированных линейных множителей и
квадратных трехчленов то есть: ![]() .
.
Доказательство:
По Т1 можно представить в виде произведения многочленов 1 степени и 2 степени с мнимыми корнями с учетом того, что корни могут оказаться кратными то есть некоторые неприводимые над С многочлены в разложении могут повторятся то в общем случае запевшим:
![]()
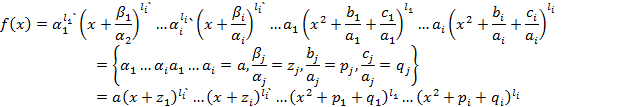
В результате получим, что f(x) удовлетворяет (*).
■
