Элементы теории корреляций

1. Введение. В математическом анализе мы имеем дело с функциональной зависимостью между двумя переменными величинами, при которой каждому значению одной из них соответствует единственное значение другой. Однако часто приходится иметь дело с более сложной зависимостью, чем функциональная. Такая зависимость возникает тогда, когда одна из величин зависит не только от другой, но и от ряда прочих меняющихся факторов, среди которых могут быть и общие для обеих величин.

Так, например, с увеличением высоты сосны увеличивается диаметр се ствола. Однако если исследовать эту зависимость по опытным данным, то может оказаться что для отдельных сосен с большей высотой диаметр ствола окажется меньше, чем для сосен с меньшей высотой. Это объясняется тем, что диаметр ствола сосны зависит не только от высоты, но и от других факторов (например, от свойств почвы, количества влаги, степени освещенности и т. д.). Это обстоятельство наглядно видно из таблицы, в которой приведены значения диаметров ствола сосны в зависимости от ее высоты. В каждой клетке этой таблицы помещено число сосен, имеющий соответствующие диаметр ствола и высоту¹⁹. Так, например, количество сосен с высотой 24м и с диаметром ствола 26см и равно двум.

Высота, м Диаметр, см	22,5 – 23,5 (23)	23,5 – 24,5 (24)	24,5 – 25,5 (25)	25,5 – 26,5 (26)	26,5 – 27,5 (26)	27,5 – 28,5 (28)
20 – 24 (22)	2						2
24 – 28 (26)		2	1	2			5
28 – 32 (30)		2	2		1		5
32 – 36 (34)			2	1			3
36 – 40 (38)			1	1	2		4
40 – 44 (42)				2		3	5
44 – 48 (46)					2		2
	2	4	6	6	5	3	26

Ниже приведены средние значения диаметра ствола сосны в зависимости от высоты.

Высота, м	23	24	25	26	27	28
Средний диаметр, см	22	28	32	34,7	39,6	42

Мы видим, что с увеличением высоты сосны в среднем растет диаметр её ствола. Однако сосны заданной высоты имеют распределение диаметров с довольно большим рассеянием. Если в среднем, например, 26-метровые сосны толще, чем 25-метровые, то для отдельных сосен это соотношение нарушается.

В рассмотренном примере мы имеем две случайные величины: ξ – высота сосны и η – диаметр ее ствола. Каждому значению х величины ξ соответствует множество значений η, которые она может принимать с различными вероятностями. Говорят, что между ξ и η существует корреляционная зависимость.

Этот пример приводит нас к следующему определению: две случайные величины ξ и η находятся в корреляционной зависимости, если каждому значению одной из этих величин соответствует определенное распределение вероятностей другой.

Для характеристики корреляционной зависимости между случайными величинами вводится понятие коэффициента корреляции.

2. Коэффициент корреляции. Как мы знаем, если ξ и η – независимые случайные величины, то по свойству математического ожидания (§ 4, п. 1)

M(∙) = M()∙M(). (72)

Если же ξ и η не являются независимыми случайными величинами, то, вообще говоря, M(∙) ≠ M()∙M().

За меру связи (зависимости) двух случайных величин ξ и η принято считать безразмерную величину R(ξ, η), определяемую соотношением

(73)

и называемую коэффициентом корреляции.

Рассмотрим некоторые свойства коэффициента корреляции.

Если ξ и η – независимые случайные величины, то коэффициент корреляции равен нулю.

Это свойство непосредственно вытекает из соотношений (72) и (73). Заметим, что обратное утверждение, вообще говоря, неверно, т. е. если R(ξ, η) = 0, то отсюда еще не следует, что ξ и η независимы.

Заметим без доказательства, что |R(ξ, η)| ≤ 1. При этом если |R(ξ, η)| = 1, то между случайными величинами ξ и η имеет место функциональная, а именно линейная зависимость.

Замечание. Как показано в § 3, п. 6 раздела теории вероятностей, двумерная случайная величина (ξ₁, ξ₂) распределена нормально, если плотность φ(х, у) распределения системы величин ξ₁, и ξ₂ имеет вид

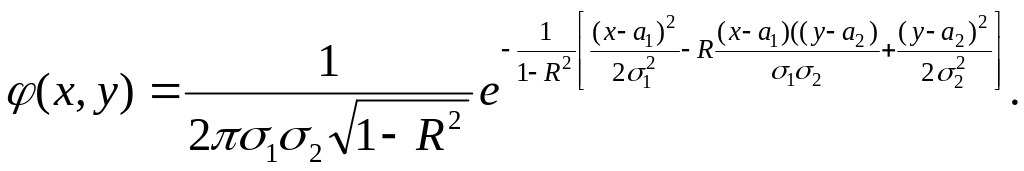
Можно показать, что постоянная R равна коэффициенту корреляции величин ξ₁, и ξ₂ , т.е. R(ξ, η) = R. Следует заметить, что в случае, когда система величин ξ₁, и ξ₂ распределена нормально и коэффициент корреляции R(ξ, η) = R = 0, то величины ξ₁, и ξ₂ независимы (см. § 3, п. 6).

3. Функции и линии регрессии. Пусть ξ и η – две случайные непрерывные величины, находящиеся в корреляционной зависимости. Это значит, что каждому значению х случайной величины ξ соответствует вполне определенное распределение вероятностей величины η. Плотность φ_x(у) распределения величины η при условии, что ξ=х, называется условной плотностью распределения случайной величины η.

Вычислим для данного случая так называемое условное математическое ожидание М_х(η) величины η при условии, что ξ = х. Согласно определению математического ожидания непрерывной случайной величины, имеем

[см. формулу (40)]. Каждому возможному значению х случайной величины ξ соответствует определенное значение условного математического ожидания М_х(η). Таким образом, мы получаем функцию М_х(η) = f(x) переменной х. Эта функция y = f(x) называется функцией регрессии величины η на ξ, а ее график – линией регрессии η на ξ. Аналогично определяется условное математическое ожидание величины ξ при условии, что η = у:

где φ_y(x) – условная плотность вероятности случайной величины ξ при условии, что η = y.

Функция x = g(y) называется функцией регрессии величины ξ на η, а ее график – линией регрессии ξ на η.

Следует иметь в виду, что функции y = f(x) и x = g(y) не являются обратными по отношению друг к другу.

Если обе функции М_х(η) = f(x) и М_y(ξ) = g(y) линейны, то линиями регрессии являются прямые. В этом случае говорят, что случайные величины ξ и η связаны линейной корреляционной зависимостью. Можно показать, что уравнение прямой регрессии η на ξ имеет следующий вид:

(74)

где у = М_х(η) – условное математическое ожидание случайной величины η при ξ = х. Аналогично записывается уравнение прямой регрессии ξ на η:

(75)

где х = М_у(ξ) – условное математическое ожидание ξ при η = у. Величины

(76)

называются коэффициентами регрессии соответственно η на ξ и ξ на η.

Из формул (76) следует, что

(77)

Равенство (77) показывает, что оба коэффициента регрессии имей одинаковые знаки. Если они положительны (отрицательны), то с возрастанием аргумента возрастают (убывают) соответствующие условные математические ожидания.

Если R(ξ, η) = 0, то, как следует из уравнений (74) и (75), у = М_х(η) = М(η) и х = М_у(ξ) = М(ξ), т. е. в этом случае условные математические ожидания постоянны и равны соответствующим математическим ожиданиям случайных величин ξ и η.

Замечание. Можно доказать, что если система двух случайных величин имеет нормальное распределение, то эти величины находятся в линейной корреляционной зависимости.

4. Анализ линейной корреляции по опытным данным. Одной из задач математической статистики является исследование корреляционной зависимости между случайными величинами. Пусть проведено п опытов, в результате которых получены следующие значения системы величин (ξ, η):

(x₁, y₁), (x₂, y₂), …, (x_i, y_i), …, (x_n, y_n).

За приближенные значения М(ξ), М(η), D(ξ), D(η), принимают их выборочные значения , , , [см. формулы (66) и (67)]:

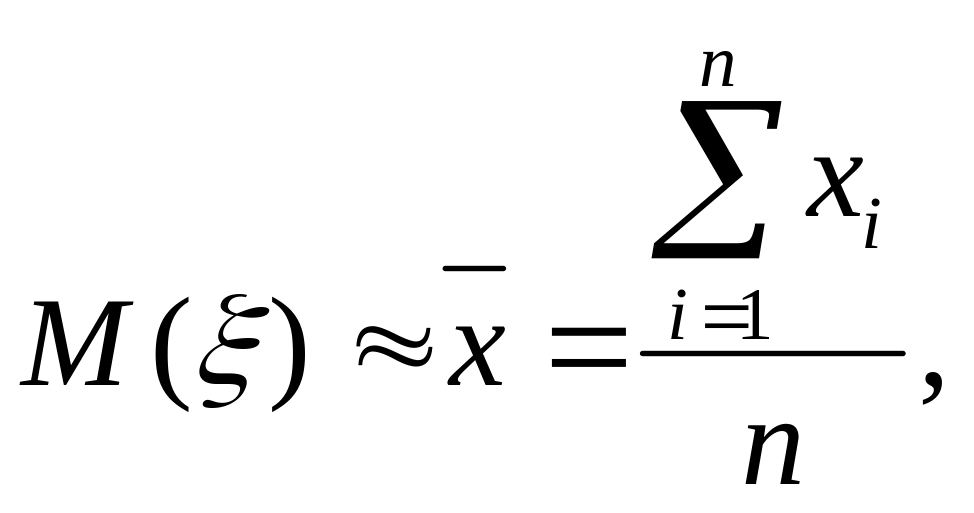
(78)

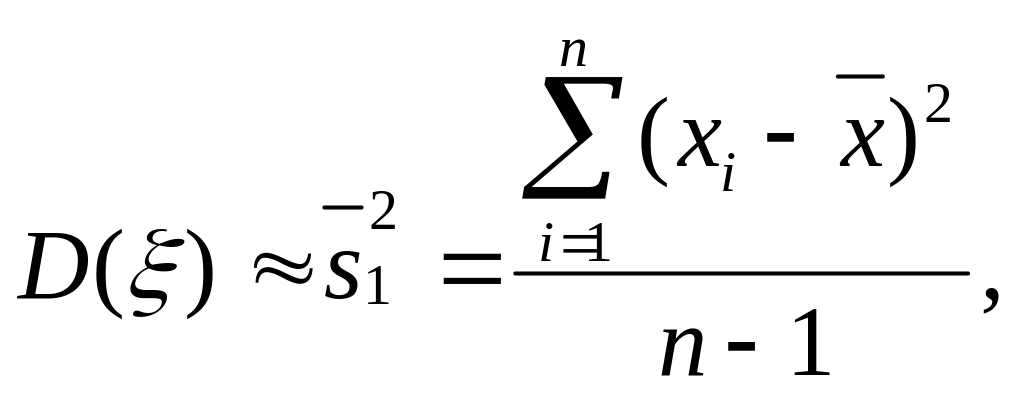
(79)

Выборочным коэффициентом корреляции называют число , определяемое соотношением

(80)

Можно показать, что сходится по вероятности к коэффициенту корреляции R(ξ, η).

Заменяя в соотношениях (76) величины σ(ξ), σ(η) и R(ξ, η) их выборочными значениями , и [см. формулы (79), (80)], получим приближенные значения коэффициентов регрессии:

(81)

Подставляя в уравнения (74) и (75) приближенные значения коэффициентов регрессии и используя соотношения (78) и (81), получим уравнения эмпирических прямых регрессий:

η на ξ:

(82)

ξ на η:

(83)

При большом числе опытов для упрощения подсчета значений , , , и коэффициента корреляции поступим следующим образом (см. п. 2, замечания 2 и 3 данного раздела).

Диапазоны изменения наблюдаемых значений случайных величин ξ и η разобьем соответственно на интервалы

]X₀, X₁[, ]X₁, X₂[, …, ]X_i-1, X_i[, …, ]X_k-1, X_k[

и

]Y₀, Y₁[, ]Y₁, Y₂[, …, ]Y_j-1, Y_j[, …, ]Y_s-1, Y_s[.

Каждое из наблюдаемых значений ξ (η), попавших в i-й (j-й) интервал, считаем приближенно равным середине этого интервала c_i (d_j). Пусть m'_i (m''_j) – и число значений ξ (η), попавших в i-й (j-й) интервал, а х₀ и у₀ – произвольные числа, близкие к серединам диапазонов изменения значений ξ и η. Полагая u_i = c_i – x₀ и v_j = d_j – y₀ и используя формулы (70) и (71), получим:

, ,

, , (84)

где

,

, .

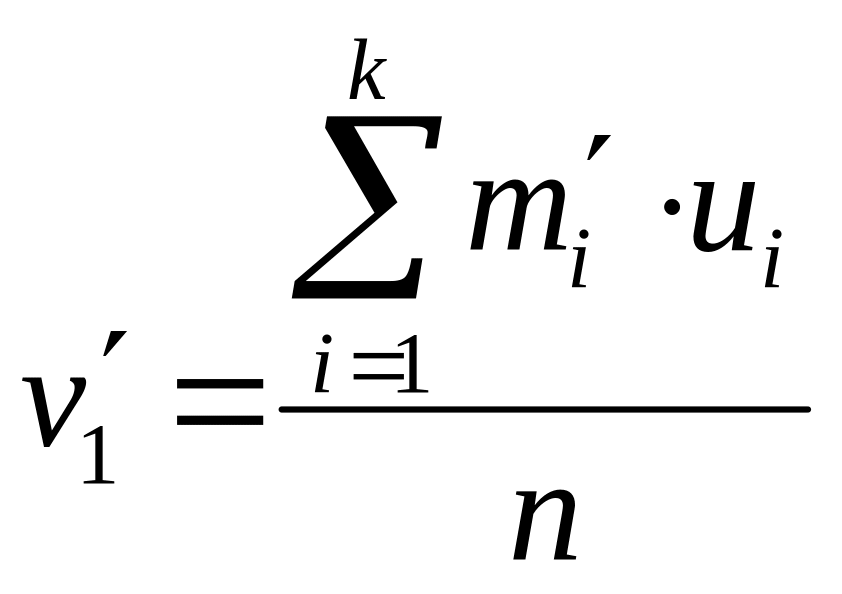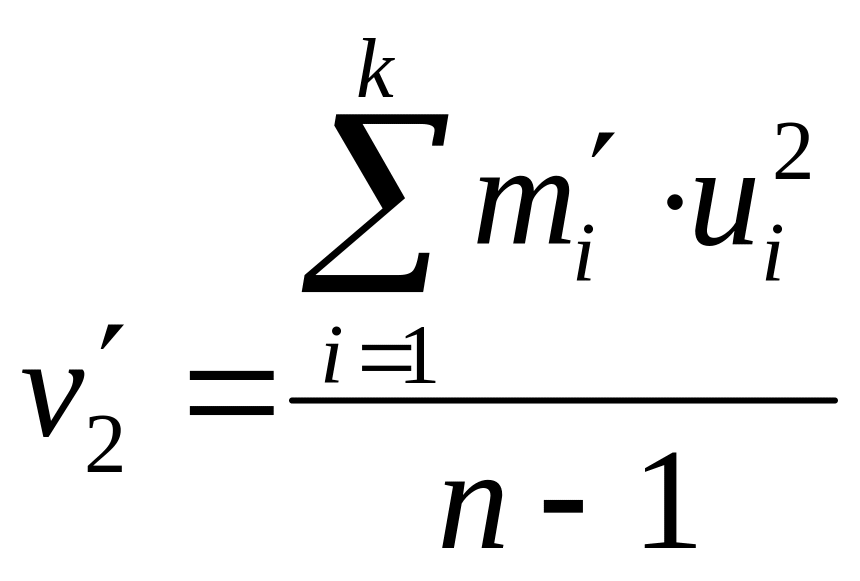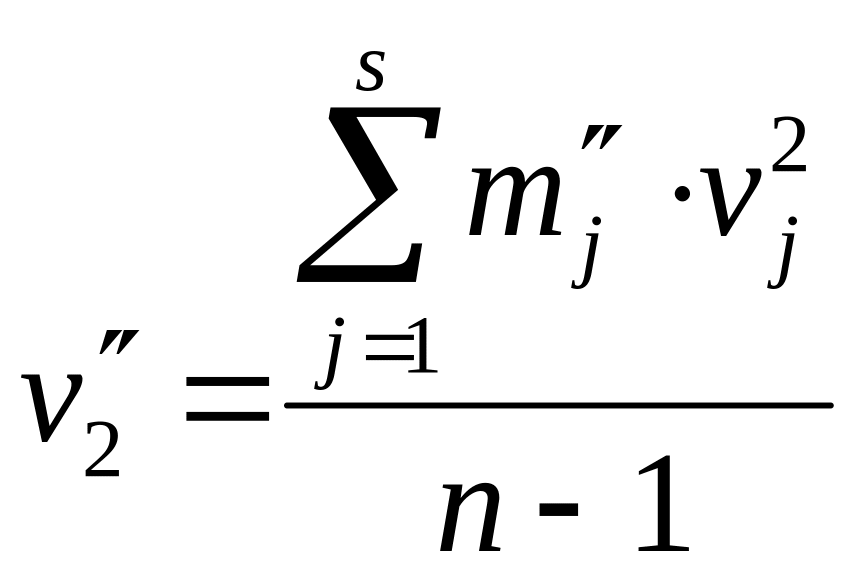Для подсчета выборочного коэффициента корреляции по формуле (80) сначала запишем выражение в новых переменных u_i = c_i – x₀ и v_j = d_j – y₀. Обозначим через т_ij число наблюдаемых значений пар (ξ, η), у которых значения ξ попали в i-й интервал ]X_i-1, X_i[, а значения η – j-й интервал ]Y_j-1, Y_j[. Каждое из этих значений ξ и η заменим соответствующими серединами c_i и d_j интервалов ]X_i-1, X_i[ и ]Y_j-1, Y_j[. Тогда

,

где сумма в правой части равенства распространена на все возможные пары чисел (i, j), причем i пробегает значения от 1 до k, a j – от 1 до s. После преобразований в результате получим

.

Итак, окончательная расчетная формула для выборочного коэффициента корреляции имеет вид

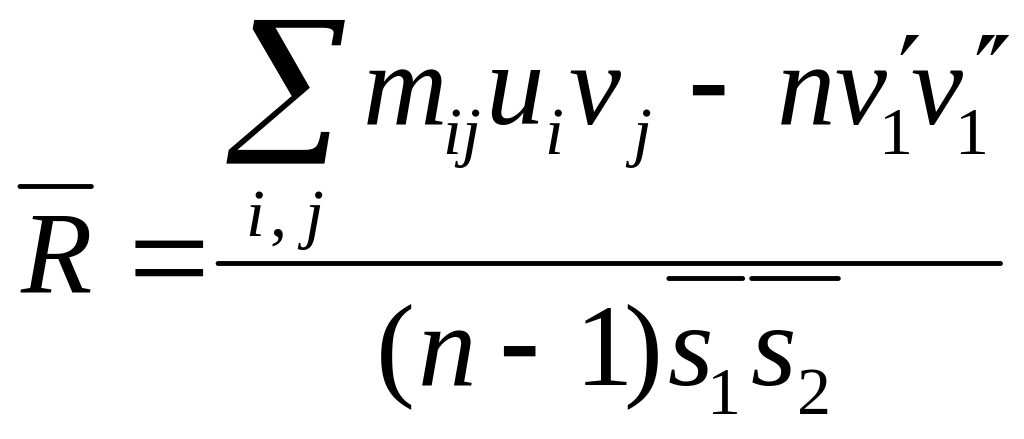. (85)

Пример. Для выяснения зависимости между диаметром ствола (η) сосны и её высотой (ξ) было исследовано 26 сосен. Наблюдаемые значения высоты сосен колеблются в границах от 22,5 до 28,5 м, диаметр ствола – от 20 до 48 см. Разбивая диапазон изменения высоты сосны на интервалы длиной 1 м, а диапазон изменения диаметра ствола на интервалы длиной 4 см, получим таблицу, приведенную на стр. 42 (см. п.1 данного раздела). Эта таблица называется корреляционной. В каждой её клетке стоит число сосен, диаметр ствола и высота которых находится в указанных границах (числа т_ij). При подсчете статистических характеристик примем высоту всех сосен, попавших в данный интервал, равной середине с_i этого интервала, а диаметр ствола – равным середине d_j соответствующего интервала. Подсчет выборочных средних, дисперсий и коэффициента корреляции производим по формулам (84) и (85). Для подсчета , , и составляем две вспомогательные таблицы 1 и 2, принимая x₀=25 и y₀=34, т.е. u_i = c_i – 25 и v_j = d_j – 34.

Таблица 1

Номер интервала	Середина интервала сi высоты, м
1 2 3 4 5 6	23 24 25 26 27 28	-2 -1 0 1 2 3	2 4 6 6 5 3	4 1 0 1 4 9	-4 -4 0 6 10 9	8 4 0 6 20 27
∑			26		17	65

Таблица 2

Номер интервала	Середина интервала dj диаметра, см
1 2 3 4 5 6 7	22 26 30 34 38 42 46	-12 -8 -4 0 4 8 12	2 5 5 3 4 5 2	144 64 16 0 16 64 144	-24 -40 -20 0 16 40 24	288 320 80 0 64 320 288
∑			26		-4	1360

Из таблицы 1 для высоты сосны ξ получаем

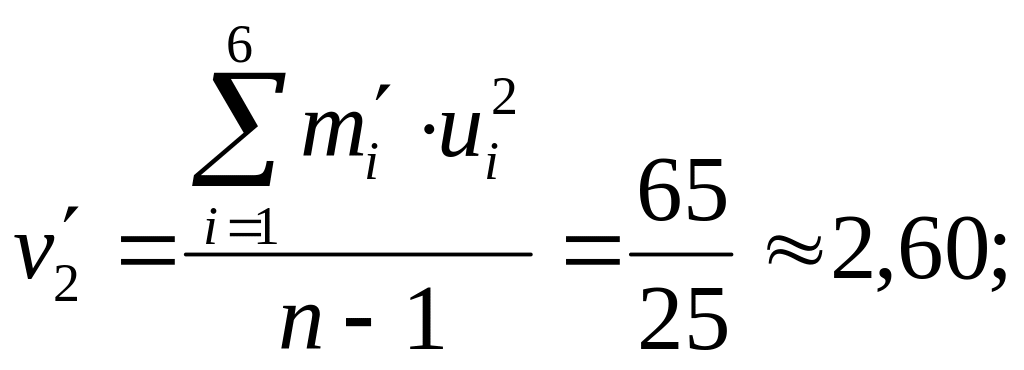
Из таблицы 2 для диаметра ствола сосны η находим

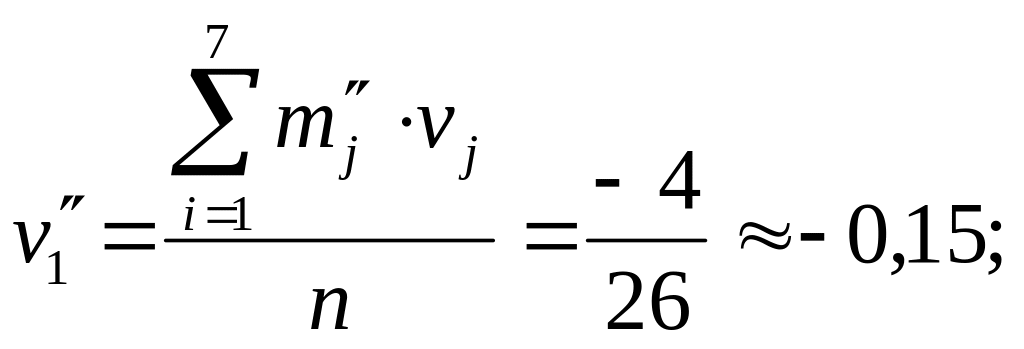
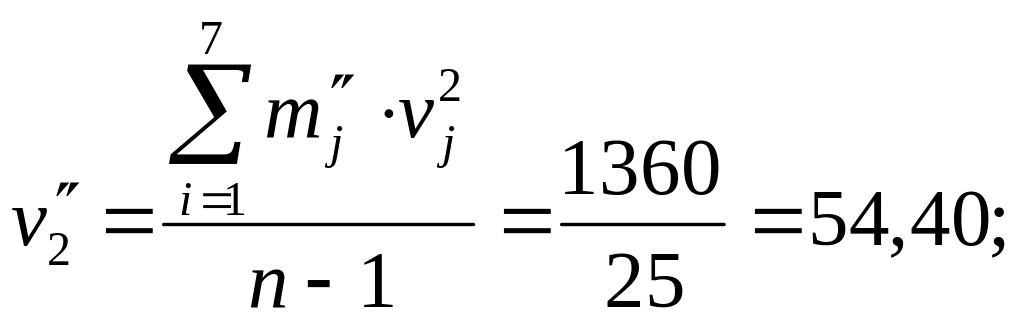
Для подсчета составляем новую таблицу 3. В каждой ее клетке (вверху справа) указано число m_ij сосен, имеющих одни и те же значения u_i и v_j, а внизу слева указано произведение m_iju_iv_j. Последний столбец состоит из суммы всех m_iju_iv_j при постоянном j. Как видно из таблицы 3,

Таблица 3

ui vj	-2	-1	0	1	2	3	∑
-12	2 48						48
-8		2 16	1 0	2 -16			0
-4		2 8	2 0		1 -8		0
0			2 0	1 0			0
4			1 0	1 4	2 16		20
8				2 16		3 72	88
12					2 48		48
							204

Используя формулу (85), найдем выборочный коэффициент корреляции:

По формулам (81) находим приближенные значения коэффициентов регрессии:

По формулам (82) и (83) найдем эмпирические уравнения прямых регрессий. Уравнение прямой регрессии η на ξ имеет вид

y – 33,85 = 3,81(x – 25,65), или y = 3,81x – 63,88.

Это уравнение дает зависимость среднего значения диаметра ствола от его длины. Уравнение прямой регрессии ξ на η имеет вид

x – 25,65 = 0,15(y – 33,85), или x = 0,15y + 21,57.

Последнее уравнение дает зависимость среднего значения длины ствола от его диаметра.