Приложение

Таблица 1

Значения функции

x	φ(x)	x	φ(x)	x	φ(x)	x	φ(x)
0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95	0,3989 0,3984 0,3970 0,3945 0,3910 0,3867 0,3814 0,3752 0,3683 0,3605 0,3521 0,3429 0,3332 0,3230 0,3123 0,3011 0,2897 0,2780 0,2661 0,2541	1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 1,45 1,50 1,55 1,60 1,65 1,70 1,75 1,80 1,85 1,90 1,95	0,2420 0,2299 0,2179 0,2059 0,1942 0,1826 0,1714 0,1604 0,1497 0,1394 0,1295 0,1200 0,1109 0,1023 0,0940 0,0863 0,0790 0,0721 0,0656 0,0596	2,00 2,05 2,10 2,15 2,20 2,25 2,30 2,35 2,40 2,45 2,50 2,55 2,60 2,65 2,70 2,75 2,80 2,85 2,90 2,95	0,0540 0,0488 0,0440 0,0396 0,0355 0,0317 0,0283 0,0252 0,0224 0,0198 0,0175 0,0154 0,0136 0,0119 0,0104 0,0091 0,0079 0,0069 0,0060 0,0051	3,00 3,05 3,10 3,15 3,20 3,25 3,30 3,35 3,40 3,45 3,50 3,55 3,60 3,65 3,70 3,75 3,80 3,85 3,90 3,95 4,00	0,0044 0,0038 0,0033 0,0028 0,0024 0,0020 0,0017 0,0015 0,0012 0,0010 0,0009 0,0007 0,0006 0,0005 0,0004 0,0003 0,0002 0,0002 0,0002 0,0002 0,0001

Таблица 2

Значения функции

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80	0,00000 0,01994 0,03983 0,05962 0,07926 0,09871 0,11791 0,13683 0,15542 0,17364 0,19156 0,20884 0,22575 0,24115 0,25804 0,27337 0,28814	0,85 0,90 0,95 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 1,45 1,50 1,55 1,60 1,65	0,30234 0,31594 0,32894 0,34134 0,35314 0,36433 0,37493 0,38493 0,39435 0,40320 0,41149 0,41924 0,42647 0,43319 0,43943 0,44520 0,45053	1,70 1,75 1,80 1,85 1,90 1,95 2,00 2,05 2,10 2,15 2,20 2,25 2,30 2,35 2,40 2,45 2,50	0,45543 0,45994 0,46407 0,46784 0,47128 0,47441 0,47725 0,47982 0,48214 0,48422 0,48610 0,48778 0,48928 0,49061 0,49180 0,49256 0,49379	2,55 2,60 2,65 2,70 2,75 2,80 2,85 2,90 2,95 3,00 3,20 3,40 3,60 3,80 4,00 4,50 5,00	0,49461 0,49534 0,49598 0,49653 0,49702 0,49744 0,49781 0,49813 0,49841 0,49865 0,49931 0,49966 0,499841 0,499928 0,499968 0,499997 0,500000

1 Событие А₁А₂Аз можно представить как совмещение двух событий: события C=A₁A₂ и события А₃.

2 Т. Бейес (ум. 1763) —английский математик.

3 Я. Бернулли (1654 – 1705) – швейцарский математик.

4 П. Лаплас (1749 – 1827) – французский математик и астроном.

5 Случайные величины обозначаются малыми буквами греческого алфавита: ξ, η, ς, ….

6 Здесь и в дальнейшем введены обозначения , .

7 Можно показать, что F(х_i) = F(х_i – 0), т.е. что функция F(х_i) непрерывна слева в точке х_i.

8 Функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва 1 рода.

9 Дифференцирование интеграла с бесконечной нижней границей и переменной верхней границей можно свести к дифференцированию интегралов с конечной нижней границей и переменной верхней границей. В самом деле,

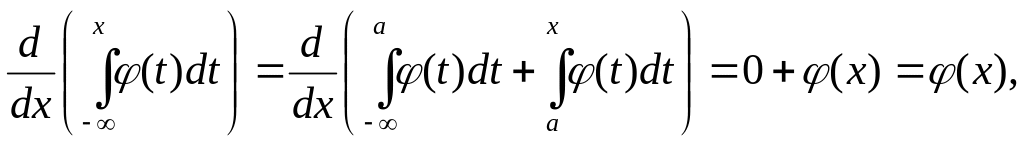
так как интеграл есть величина постоянная.

10 См. сноску на с. 14

11 В случае, если множество возможных значений дискретной случайной величины образует бесконечную последовательность х₁, х₂, …, х_п, то математическое ожидание этой случайной величины определяется как сумма ряда , причем требуется, чтобы этот ряд абсолютно сходился,

12 Под суммой (произведением) двух случайных величин  и  понимают случайную величину  =  +  (=∙), возможные значения которой состоят из сумм (произведений) каждого возможного значения величины  и каждого возможного значения величины .

13 Казалось бы естественным рассматривать не квадрат отклонения, а просто отклонение  – M() случайной величины от ее математического ожидания. Однако математическое ожидание этого отклонения равно нулю, так какM[ – M()] = M() – M[M()] = M() – M() = 0. Здесь мы воспользовались тем, что M() постоянно, а математическое ожидание постоянной есть эта постоянная. Можно было бы принять за меру рассеяния математическое ожидание модуля отклонения случайной величины от ее математического ожидания: M[| – M()|]. Однако, как правило, действия, связанные с абсолютными величинами, приводят к громоздким вычислениям.

14 Последнее утверждение можно получить просто из свойств математического ожидания и дисперсии. Так, например, М(η) = М(А + Вξ) = М(A) + ВM(ξ) = А + Ва.

15 П. Л. Чебышев (1821—1894) — выдающийся русский математик.

16 Л. М. Ляпунов (1857-1918) – выдающийся русский математик.

17 Расчет по формуле (63) дает удовлетворительные по точности результаты при n ≥ 30

18 Для простоты вычислений, как это обычно делается, за х₀ мы выбрали число, близкое к середине диапазона изменения наблюдаемых значений.

19 При подсчетах мы принимаем диаметры стволов и высоты всех сосен, попавших в данный интервал, равными серединам соответствующих интервалов.

47