§4. Числовые характеристики случайных величин

В теории вероятностей и во многих ее приложениях большое значение имеют различные числовые характеристики случайных величин. Основными из них являются математическое ожидание и дисперсия.

1. Математическое ожидание случайной величины и его свойства. Рассмотрим сначала следующий пример. Пусть на завод поступила партия, состоящая из N подшипников. При этом:

m₁ – число подшипников с внешним диаметром x₁,

m₂ – число подшипников с внешним диаметром x₂,

. . . . . . .

m_n – число подшипников с внешним диаметром x_n.

Здесь т₁ + т₂-+-…+т_п = N. Найдем среднее арифметическое значение х_ср внешнего диаметра подшипника. Очевидно,

Внешний диаметр вынутого наудачу подшипника можно рассматривать, как случайную величину ξ, принимающую значения х₁ х₂, ..., х_п с соответствующими вероятностями p₁ = m₁/N, р₂ = т₂/N, … р_п = m_n/N, так как вероятность р_i появления подшипника с внешним диаметром x_i равна m_i/N. Таким образом, среднее арифметическое значение х_ср внешнего диаметра подшипника можно определить с помощью соотношения:

Пусть ξ – дискретная случайная величина с заданным законом распределения вероятностей P(ξ = x_i) = p_i.

Значения ξ	х1	х2	...	хn
Вероятности P(ξ = xi)	p1	p2	…	pn

Математическим ожиданием М(ξ) дискретной случайной величины называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т. е.¹¹

(39)

Возвращаясь к разобранному выше примеру, мы видим, что средний диаметр подшипника равен математическому ожиданию случайной величины ξ – диаметру подшипника.

Математическим ожиданием М(ξ) непрерывной случайной величины ξ с плотностью распределения (х) называется число, определяемое равенством:

(40)

При этом предполагается, что несобственный интеграл, стоящий в правой части равенства (40), существует.

Рассмотрим свойства математического ожидания. При этом ограничимся доказательством только первых двух свойств, которое проведем для дискретных случайных величин.

1⁰). Математическое ожидание постоянной С равно этой постоянной.

Доказательство. Постоянную С можно рассматривать как случайную величину ξ, которая может принимать только одно значение С с вероятностью, равной единице. Поэтому М(ξ) = С∙1 = С.

2°). Постоянный множитель можно выносить за знак математического ожидания, т. е.

М(kξ) = k М(ξ).

Доказательство. Используя соотношение (39), имеем

Следующие два свойства приведем без доказательства.

3°). Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:

М(ξ₁+ ξ₂+…+ ξ_n) = М(ξ₁) + M(ξ₂) +…+ M(ξ_n). (41)

4°). Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин¹²:

M(∙) = M()∙M(). (42)

2. Дисперсия и ее свойства. Среднее квадратическое отклонение. Во многих практически важных случаях существенным является вопрос о том, насколько велики отклонения ξ – М(ξ) случайной величины от ее математического ожидания. Предварительно рассмотрим пример. Пусть две случайные величины  и  заданы следующими рядами распределения:

Значения ξ	-0,2	-0,1	0,1	0,2	Значения 	-50	-40	40	50
Вероятности p(x)	0,25	0,25	0,25	0,25	Вероятности p(x)	0,25	0,25	0,25	0,25

Легко убедиться в том, что математические ожидания этих величин одинаковы и равны нулю:

М () = (-0,2)∙0,25 + (-0,1)∙0,25 + 0,1∙0,25 + 0,2∙0,25 = 0,

М () = (-50)∙0,25 + (-40)∙0,25 + 40∙0,25 + 50∙0,25 = 0.

Однако разброс значений этих величин относительно их математического ожидания неодинаков. В первом случае значения, принимаемые случайной величиной ξ близки к ее математическому ожиданию, а во втором случае для величины  – далеки от него. Для оценки разброса (рассеяния) значений случайной величины около её математического ожидании введена следующая числовая характеристика – дисперсия.

Дисперсией D(ξ) случайной величины ξ называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания¹³ *:

D() = M[ – M()]². (43)

Пусть  – дискретная случайная величина, принимающая значения х₁, х₂,…, х_n соответственно с вероятностями р₁, р₂, …, p_n. Очевидно, случайная величина [ – M()]² принимает значения [х₁ – M()]², [х₂ – M()]², …, [х_п – M()]² с теми же вероятностями р₁, р₂, …, p_n. Следовательно, согласно определению математического ожидания дискретной случайной величины, имеем

(44)

Если же  – непрерывная случайная величина с плотностью распределения (х), то по определению

(45)

Принимая во внимание определение дисперсии и свойства математического ожидания, имеем

D() = M[ – M()]² = M{² – 2∙M() + [M()]²} = M(²) – 2M[∙M()] + M[M()]².

Так как М() и [М()]² – постоянные, то используя свойства математического ожидания, получим: M[∙M()] = M()∙M() и M[M()]² = [M()]². Следовательно,

D() = M(²) – 2M()∙M() + [M()]²,

откуда окончательно находим

D() = M(²) – [M()]². (46)

Рассмотрим теперь свойства дисперсии.

1°). Дисперсия постоянной равна нулю.

Доказательство. Пусть ξ = С. По формуле (46) имеем

D(С) = M(С²) – [M(С)]² = С² – С² = 0,

так как математическое ожидание постоянной есть эта постоянная: М(С) = С, М(С²) = С².

2°). Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

D(kξ) = k² D(ξ). (47)

Доказательство. На основании соотношения (46) можно записать:

D(k) = M[(k)²] – [M(k)]².

Так как M[(k)²] = M(k²²) = k² M(²) и [M(k)]² = [kM()]² = k²[M()]²,

то D(kξ) = k²{M(²) – [M()]²} = k² D(ξ).

3°). Если  и η – независимые случайные величины, то дисперсия суммы этих величин равна сумме их дисперсий:

D( + η) = D() + D(η). (48)

Доказательство. По формуле (46) имеем:

D( + η) = М [( + η)²] – [М( + η)]².

Но М[( + η)²] = М(² + 2∙η + η²) = М(²) + 2M(∙η) + M(η²). Так как  и η – независимые случайные величины, то M(∙η) = M()∙M(η). Следовательно,

М[( + η)²] = М(²) + 2M() M(η) + M(η²).

Далее, M( + η) = M() + M(η); поэтому

[М( + η)]² = [М() +M(η)]² = [М()]² + 2М()∙M(η) + [М(η)]².

Таким образом:

D( + η) = М(²) + 2M() M(η) + M(η²) – [М()]² – 2М()∙M(η) – [М(η)]² =

= {М(²) – [М()]²} + { M(η²) – [М(η)]²}.

Но

M(²) – [М()]² = D(), M(η²) – [М(η)]² = D(η).

Следовательно, D( + η) = D() + D(η).

Замечание. Свойство 3° распространяется на любое конечное число попарно независимых случайных величин:

D(₁ + ₂ + … + _n) = D(₁) + D(₂) + … + D(_n).

Средним квадратическим отклонением () случайной величины  называется корень квадратный из ее дисперсии:

(49)

Среднее квадратическое отклонение () имеет ту же размерность, что и случайная величина.

Пример 1. Случайная величина  – число очков, выпадающих при однократном бросании игральной кости (см. §3, п.1, пример 1). Определить М(), D() и ().

Решение. Используя формулы (39), (44) и (49), соответственно получим:

Пример 2. Случайная величина  – число наступлений события А при одном испытании, причем Р(А) = р (см. §3, п.1, пример 2). Найти М() и D().

Решение. Величина  принимает два значения 0 и 1 соответственно с вероятностями q = = 1 – р и р. Поэтому по формулам (39) и (44) находим:

М() = 0(1 – р) + 1 р = р, D() = (0 – р)²(1 – р) + (1 – р)² р = р(1 – р) = р q,

Пример 3. Случайная величина т. – число наступлений события А в п независимых опытах, причем вероятность наступления события А в каждом опыте равна р. Найти М(т), D(т) и (т).

Решение. Пусть _i – случайная величина, принимающая значения 1 или 0 в зависимости от того, происходит или не происходит событие А в i-м опыте. Тогда m = ₁ + ₂ + … + _n. Ясно, что _i попарно независимы. Из результата примера 2 следует, что M(_i) = р, D(_i) = pq для любого i. На основании свойства 3° для математического ожидания и дисперсии имеем:

М(т) = М(₁ + ₂ + … + _n) = М(₁) + М(₂) + … + М(_n) = пр,

D(т) = D(₁ + ₂ + … + _n) = D(₁) + D(₂) + … + D(_n) = npq; (m) = .

Пример 4. Пусть  – случайная величина, распределенная по закону Пуассона|

(k = 0, 1, …, n, …)

[см. формулу (17)]. Найти М().

Решение. Используя соотношение (39), получим:

так как

(см. гл.XI, §3, п.5).

Пример 5. Пусть  – случайная величина, имеющая равномерное распределение с плотностью

[см. формулу (27)]. Найти М(), D() и ().

Решение. По формулам (40), (45) и (49) находим

Пусть  – нормально распределенная случайная величина с параметрами an (см. §3, п.5). Найдем M() и D().

Так как то по формуле (40) находим

Произведем в интеграле замену переменной, полагая (x – a)/σ = z; тогда x = a + σz и dx = σdz. Следовательно,

Но [см. формулу (29)]. Далее, так как функция нечетная, то по свойству нечетных функций Следовательно, M(ξ) = a.

Дисперсию находим по формуле (45):

(вычисление интеграла не приводим).

Итак, D() = σ², Таким образом, параметры а и σ для нормально распределенной случайной величины имеют простой вероятностный смысл: а – математическое ожидание, σ – среднее квадратическое отклонение.

3. Линейные функции случайных величин. Пусть  – нормально распределенная случайная величина с параметрами M(ξ) = a и σ(ξ) = σ. Тогда, если А и В – постоянные, то случайная величина η = A +Bx, линейно зависящая от x, также нормально распределена, причем¹⁴

М(η) = А + Ва, D(η) = В²σ².

Докажем это утверждение. Пусть для простоты В > 0. Оценим вероятность неравенств y₁ < η <y₁. Ясно, что эти неравенства равносильны неравенствам y₁<A+Bx< y₂, т.е. (y₁ – A)/В < x < (y₂ – A)/В. Поэтому

Так как величина x распределена нормально, то

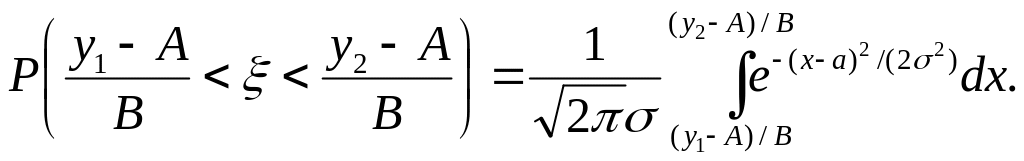
Произведем в этом интеграле замену переменной, полагая х=(у – А)/B. Тогда dх = =dy/B и, следовательно,

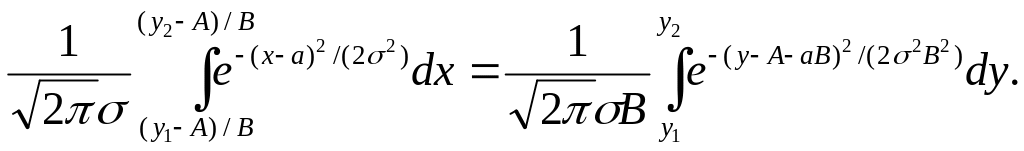
Итак,

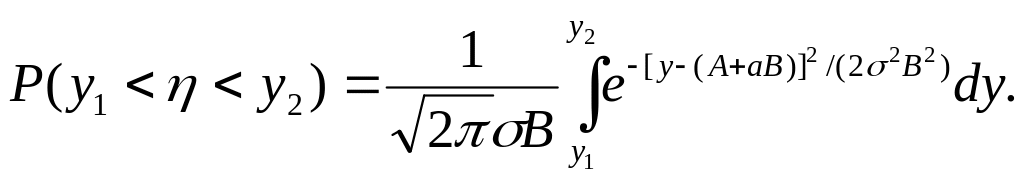
Это равенство показывает, что случайная величина η имеет нормальное распределение, причем M(η) = А + aВ и D(η) = σ²В².

Справедливо и более общее утверждение. Пусть λ₁, λ₂, … λ_n – постоянные, a x₁, x₂, … x_n – нормально распределенные попарно независимые случайные величины, причем M(ξ) = a_i и D(x). = σ_i². Тогда случайная величина η = λ₁ξ₁ + λ₂ξ₂ + … λ_nξ_n также имеет нормальное распределение, причем

M(η) = λ₁a₁ + λ₂a₂ + … + λ_na_n,

D(η) = λ₁²σ₁² + λ₁²σ₁² + … + λ_n²σ_n².

В частности, если M(ξ_i) = a, D(x_i) = σ² при любом i, то случайная величина x = (ξ₁ + +ξ₂+ … ξ_n)/n распределена нормально, причем M(ξ) = a, D(x). = σ²/n,