§ 3. Случайные величины

Понятие случайной величины является основным в теории вероятностей и ее приложениях. Случайными величинами, например, являются число выпавших очков при однократном бросании игральной кости, число распавшихся атомов радия за данный промежуток времени, число вызовов на телефонной станции за некоторый промежуток времени, отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе и т. д. Таким образом, случайной величиной называется переменная величина, которая в результате опыта может принимать то или иное числовое значение. В дальнейшем мы рассмотрим два типа случайных величин – дискретные и непрерывные.

1. Дискретные случайные величины. Рассмотрим случайную величину⁵ ξ, возможные значения которой образуют конечную или иную последовательность чисел х_1, х₂, ..., х_п, .... Пусть задана функция р(х), значение которой в каждой точке x = x_i, (i = 1, 2, ...) равно вероятности того, что величина ξ примет значение x_i.

p(х_i) =P(ξ = x). (16)

Такая случайная величина называется дискретной (прерывной). Функция p(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности х₁, х₂, ..., х_п, .... Так как в каждом из испытаний случайная величина принимает всегда какое-либо значение из области ее изменения, то

р(х₁) + р(х₂) + ... + р(х_п) + ...= 1.

Пример 1. Случайная величина ξ – число очков, выпадающих при однократном бросании игральной кости. Возможные значения ξ – числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что ξ примет любое из этих значений, одна и та же и равна 1/6. Таким образом, здесь закон распределения вероятностей есть функция p(х)= 1/6 для любого значения х из множества {1, 2, 3, 4, 5, 6}.

Пример 2. Пусть случайная величина η – число наступлений события А при одном испытании, причем P(A) = p. Множество возможных значений η состоит из двух чисел 0 и 1: η = 0, если событие А не произошло, и η = l, если событие А произошло. Таким образом

р(0) = Р(η = 0) = Р(Ā) = 1 – р = q, р(1) = Р(η = 1) = Р(А) = р.

Предположим, что производится п независимых испытаний, в результате каждого из которых может наступить или не наступить событие А. Пусть вероятность наступления события А при каждом испытании равна р. Рассмотрим случайную величину ξ – число наступлений события А при п независимых испытаниях. Область изменения ξ состоит из всех целых чисел от 0 до п включительно. Закон распределения вероятностей р(т) определяется формулой Бернулли (13'):

Закон распределения вероятностей по формуле Бернулли часто называют биномиальным, так как Р_п(т) представляет собой m-й член разложения бинома (p + q)^m.

Пусть случайная величина ξ может принимать любое целое неотрицательное значение, причем

(k = 0, 1, 2, …, n, …), (17)

где λ – некоторая положительная постоянная. В этом случае говорят, что случайная величина ξ распределена по закону Пуассона. Заметим, что при k = 0 следует положить 0! = 1.

Как мы знаем, при больших значениях числа п независимых испытаний вероятность Р_n(т) наступления т раз события А удобнее находить не по формуле Бернулли, а по формуле Лапласа [см. формулу (15)]. Однако последняя дает большие погрешности при малой вероятности р появления события А в одном испытании. В этом случае для подсчета вероятности Р_п(т) удобно пользоваться формулой Пуассона, в которой следует положить λ = пр. Формулу Пуассона можно получить как предельный случай формулы Бернулли при неограниченном увеличении числа испытаний п и при стремлении к нулю вероятности р = λ/п.

Пример 3. На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что деталь окажется бракованной, равна 0,001 Какова вероятность того, что среди прибывших деталей будет 5 бракованных?

Решение. Здесь λ = пр= 1000∙0,001 = 1. По формуле (17) находим

Распределение Пуассона часто встречается и в других задачах. Например, если телефонистка в среднем за один час получает N вызовов, то, как можно показать, вероятность Р(k) того, что в течение одной минуты она получит k вызовов, выражается формулой Пуассона, если положить λ = N/60:

.

Если возможные значения случайной величины ξ образуют конечную последовательность х₁, х₂, …, х_п, то закон распределения вероятностей случайной величины задают в виде следующей таблицы, в которой p_i= P(ξ=x_i) и :

Значения ξ	х1	х2	…	xn
Вероятности р(х1)	p1	p2	…	pn

Э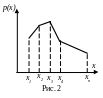 тy таблицу называют рядом распределения случайной величины ξ. Наглядно функцию р(х) можно изобразить в виде графика. Для этого используется плоская прямоугольная система координат. По оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – значения функции p(х_i) =P(ξ = x).

График функции р(х) изображен на рис. 2. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником распределения.

П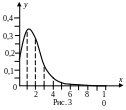 ример 4. Пусть событие А – появление одного очка при бросании игральной кости; P(A) = 1/6..Рассмотрим случайную величину ξ – число наступлений события А при десяти бросаниях игральной кости. Значения функции p(x) (закона распределения) приведены в следующей таблице:

Значение ξ	0	1	2	3	4	5
Вероятности p(хi)	0,162	0,323	0,291	0,155	0,054	0,013
Значение ξ	6	7	8	9	10
Вероятности p(хi)	0,002	0	0	0	0

Вероятности p(х_i) вычислены по формуле Бернулли при n = 10. Для х≥7 они практически равны нулю. График функции р(х) изображен на рис. 3.

2. Функция распределения вероятностей случайной величины её свойства. Рассмотрим функцию F(x), определенную на всей числовой оси следующим образом: для каждого х значение F(х) равно вероятности того, что дискретная случайная величина примет значение, меньшее х, т. е.

F(x) = P(ξ <x). (18)

Эта функция называется функцией распределения вероятностей, или кратко, функцией распределения.

Пример 1. Найти функцию распределения случайной величины ξ приведенной в примере 1, п. 1.

Р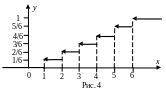 ешение. Ясно, что если x ≤ 1, то F(х) = 0, так как ξ не принимает значений, меньших единицы. Если 1<х≤2, то F(х) = Р(ξ<х) = Р(ξ = 1)=1/6, если 2<х≤3, то F(х) = Р(ξ<х) = Р(ξ<3). Но событие ξ<3 в данном случае является суммой двух несовместных событий. ξ=1 и ξ =2. Следовательно,

Итак, для 2<х≤3, имеем F(х) =1/3. Аналогично вычисляются значения функции в промежутках 3<х≤4, 4<х≤5 и 5<х≤6. Наконец, если х>6, то F(x) = l, так как в этом случае любое возможное значение ξ (1, 2, 3, 4, 5, 6) меньше чем х. График функции изображен на рис. 4.

П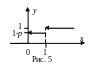 ример 2. Найти функцию распределения случайной величины η, приведенной в примере 2, п. 1.

Решение. Очевидно, что

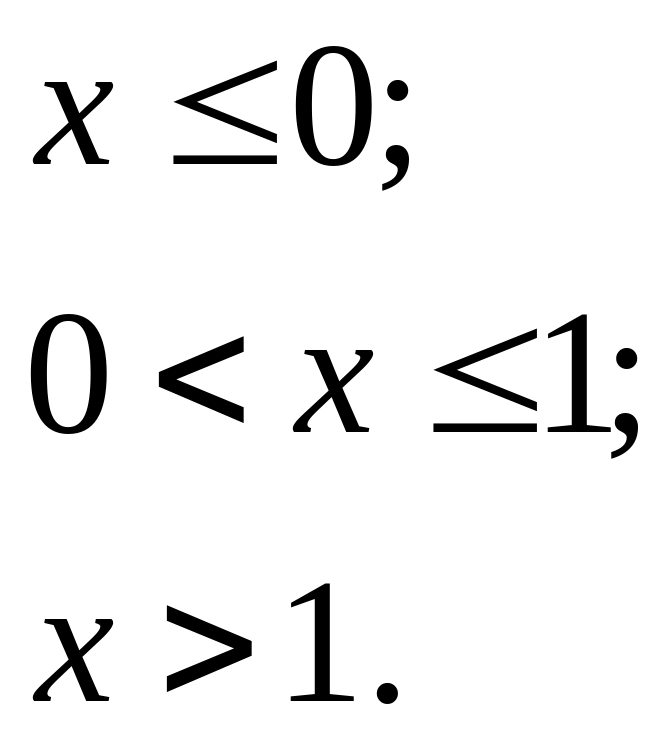
График F(х) изображен на рис. 5.

Зная функцию распределения F(х), легко найти вероятность того, что случайная величина ξ удовлетворяет неравенствам х'≤ξ<x''. Рассмотрим событие, заключающееся в том, что случайная величина примет значение, меньшее х". Это событие распадается на сумму двух несовместных событий:

1) случайная величина ξ принимает значения, меньшие х', т. е. ξ<.х';

2) случайная величина ξ принимает значения, удовлетворяющие неравенствам х'≤ξ<х".

Используя аксиому сложения, получаем

Р(ξ<х") = Р(ξ<х') + Р(х'≤ ξ<х").

Отсюда

Р(х'≤ ξ<х") = Р(ξ<х") – Р(ξ<х').

Но по определению функции распределения F(х) [см. формулу (18)], имеем P(ξ<x'') = F(х"), P(ξ<x') = F(х'); следовательно,

Р(х'≤ ξ<х") = F(х") – F(х'). (19)

Таким образом, вероятность попадания значения дискретной случайной величины в интервал х'≤ξ<x'' равна приращению функции распределения на этом интервале.

Рассмотрим основные свойства функции распределения.

1⁰). Функция распределения является неубывающей. В самом деле, пусть х'<.х". Так как вероятность любого события неотрицательна, то Р(х'≤ξ<x")≥0. Поэтому из формулы (19) следует, что F(х") – F(х') ≥ 0, т. е. F(х") ≥ F(х').

2⁰). Значения функции распределения удовлетворяют неравенствам 0≤F(x)<1. Это свойство вытекает из того, что F(х) определяется как вероятность [см. формулу (18)]. Ясно, что⁶ F(-∞ )= 0 и F(+∞) =1.

3⁰). Вероятность того, что дискретная случайная величина ξ примет одно из возможных значений х_i равна скачку функции распределения в точке х_i. Действительно, пусть х_i, – значение, принимаемое дискретной случайной величиной, и Δх>0. Полагая в формуле (19) х'= х_i, х"= х_i+Δx, получим

Р(х_i≤ ξ<х_i+Δx) = F(х_i+Δx) – F(х_i). (20)

В пределе при Δх→0 вместо вероятности попадания случайной величины на интервал х_i≤ξ<х_i+Δx, получим вероятность того, что величина ξ примет данное значение х_i:

С другой стороны, получаем , т. е. предел функции F(х) справа, так как Δх>0. Следовательно, в пределе формула (20) примет вид:

р(х_i) = F(х_i+ 0) –- F(х_i) = F(х_i+ 0) – F(х_i – 0), (21)

т. е. значение р(х_i) равно скачку функции в точке⁷ х_i. Это свойство наглядно иллюстрируется на рис. 85 и 86.

3. Непрерывные случайные величины. Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе изготовления этой детали. Такого рода случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины:

F(x) = P(ξ <x).

Таким образом, и здесь функция F(x) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение меньшее, чем х. Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величине.

Случайная величина ξ называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция⁸ (х), удовлетворяющая для любых значений х равенству

(22)

Функция (t) называется плотностью распределения вероятностей или, кратко, плотностью распределения. Если x₁<x₂, то, на основании формул (20) и (22), имеем:

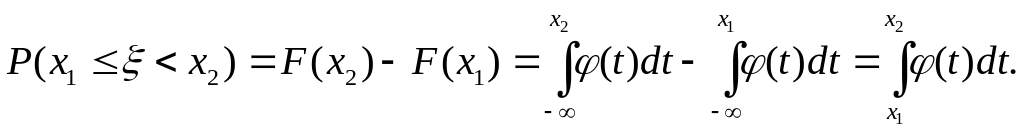
(23)

Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств х₁≤ξ<х₂ равна площади криволинейной трапеции с основанием [х₁; х₂], ограниченной сверху кривой у = φ(х) (рис. 6).

Так как F(+∞) = Р(ξ<+∞) = 1, а на основании формулы (22) , то

(24)

Пользуясь формулой (22), найдем F'(х) как производную интеграла по переменной верхней границе, считая плотность распределения (х) непрерывной⁹:

(25)

Заметим, что для непрерывной случайной величины функция распределения F(x) непрерывна в любой точке х, где функция (х) непрерывна. Это следует из того, что F(x) в этих точках дифференцируема. На основании формулы (23), полагая х_i= х, х₂= х+Δx, имеем

Р(х≤ξ<х+Δx) = F(х+Δx) – F(х) = ΔF(х).

В силу непрерывности и F(х) получим, что . Следовательно,

Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю. Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств х₁≤ξ<х₂, х₁<ξ≤х₂, х₁≤ξ≤х₂, х₁<ξ<х₂, имеют одинаковую вероятность, т. е.

Р(х₁≤ξ<х₂) = Р(х₁<ξ≤х₂) = Р(х₁≤ξ≤х₂) = Р(х₁<ξ<х₂).

В самом деле, например,

Р(х₁≤ξ<х₂) = Р(ξ=х₁) + Р(х₁<ξ<х₂) = Р(х₁<ξ<х₂),

Так как Р(ξ=х₁) = 0.

Замечание. Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытания конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания. В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение х₁, как было показано выше, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение х₁. Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.

Так, например, при изготовлении какой либо детали нас не интересует вероятность того, что ее размеры будут равны номинальным значениям. Для нас важна вероятность того, что размеры детали соответствуют допускам на изготовление.

Пример. Плотность распределения непрерывной случайной величины ξ задана следующим образом:

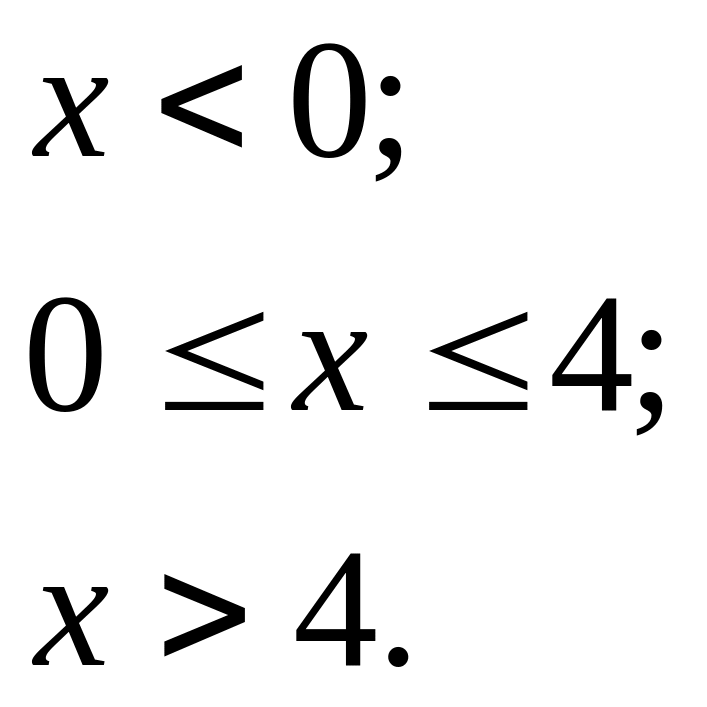
График функции (x) представлен на рис. 7. Определить вероятность того, что случайная величина ξ примет значение, удовлетворяющее неравенствам: -2≤ξ≤3. Найти функцию распределения заданной случайной величины.

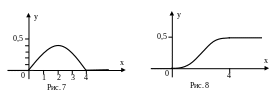
Решение. Используя формулу (23), имеем

По формуле (22) находим функцию распределения F (х) для заданной случайной величины.

Если -∞ <x≤ 0, то:

Если 0 <x≤ 4, то:

Если x> 4, то:

Объединяя решения, получим:

График функции F(x) изображен на рис. 8.

Следующие два пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин – равномерному и нормальному распределениям.

4. Равномерное распределение. Пусть сегмент [а; b] оси Ох есть шкала некоторого прибора. Допустим, что вероятность попадания указателя в некоторый отрезок шкалы пропорциональна длине этого отрезка и не зависит от места отрезка на шкале. Отметка указателя прибора есть случайная величина ξ, могущая принять любое значение из сегмента [а; b]. Поэтому P(a≤ξ≤b) = 1. Если, далее, х₁ и х₂ (х₁<х₂) – две любые отметки на шкале, то согласно условию имеем:

P(х₁≤ξ≤х₂)= k(x₂–x₁),

где k – коэффициент пропорциональности, не зависящий от х₁ и х₂, а разность x₂–x₁ – длина сегмента [х₁; х₂]. Так как при х₁= а и при х₂= b имеем P(a≤ξ≤b) = 1, то k(b–a) =1, откуда k = 1/(b – a). Таким образом,

P(х₁≤ξ≤х₂)= (x₂–x₁)/b– a). (26)

Теперь легко найти функцию F(x) распределения вероятностей случайной величины ξ.:

1). При x≤a, Р(х) = Р(ξ<x) = 0, так как ξ не принимает значений, меньших а.

2). При а<x≤b по аксиоме сложения вероятностей Р(ξ<х) = Р(ξ<а) + Р(a≤ξ<x). Согласно формуле (26), в которой принимаем х₁ = а, х₂ = х, имеем

P(a≤ξ≤х)= (x–a)/b– a);

так как Р(ξ<a) = 0, то при a<x≤b получим

F(x) = P(ξ<х)= (x–a)/b– a).

3). При x>b F(x) = 1, так как значения ξ лежат на сегменте [а; b] и, следовательно, не превосходят b. Итак, приходим к следующей функции распределения:

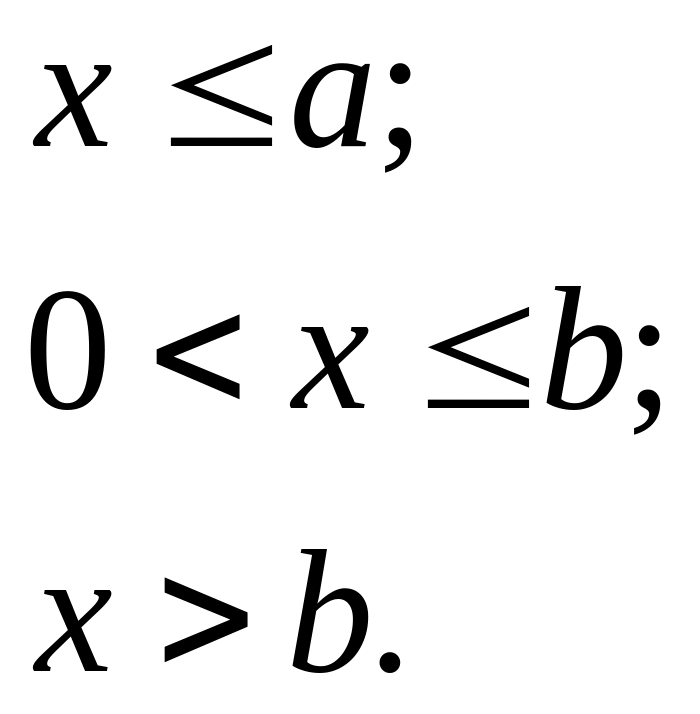
График функции F(x) представлен на рис. 9.

Плотность распределения вероятностей найдем по формуле (23). Если х<а или х>b, то (х) = F'(х) = 0. Если а<х<b, то (х)= . Таким образом,

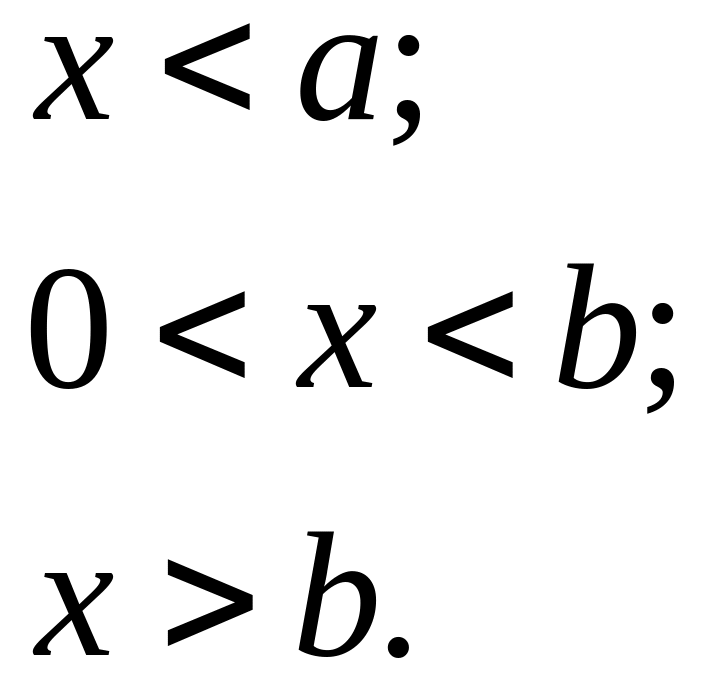(27)

График функции (х) изображен на рис. 10. Заметим, что в точках а и b функция (х) терпит разрыв.

Величина, плотность распределения которой задана формулой (27), называется равномерно распределенной случайной величиной.

5. Нормальное распределение. Говорят, что случайная величина нормально распределена или подчиняется закону распределения Гаусса, если ее плотность распределения (х) имеет вид:

(28)

где а — любое действительное число, а σ>0. Смысл параметров а и σ будет установлен в дальнейшем (см. §4, п.2). Исходя из связи между плотностью распределения (х) и функцией распределения F(x) [см. формулу (22)], имеем

График функции (х) симметричен относительно прямой х = а. Несложные исследования показывают, что функция (х) достигает максимума при х = а, а ее график имеет точки п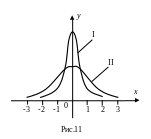 ерегиба при х₁= a + σ и х₂= a – σ. При х→±∞ график функции асимптотически приближается к оси Ох. Можно показать, что при увеличении σ кривая плотности распределения становится более пологой. Наоборот, при уменьшении σ график плотности распределения сжимается к оси симметрии. При a = 0 осью симметрии является ось Оy. На рис. 11 изображены два графика функции y = (х). График I соответствует значениям а = 0, σ = 1, а график II – значениям а = 0, σ =1/2.

Покажем, что функция (х) удовлетворяет условию (24), т. е. при любых а и σ выполняется соотношение:

Если в этом интеграле сделать замену переменной, полагая (x – a)/σ = t. Тогда

В силу четности подынтегральной функции имеем Следовательно,

Применяя правило вычисления интеграла с бесконечной верхней границей получим, что . В результате получим

(29)

Найдем вероятность P(х₁≤ξ≤х₂). По формуле (23) имеем

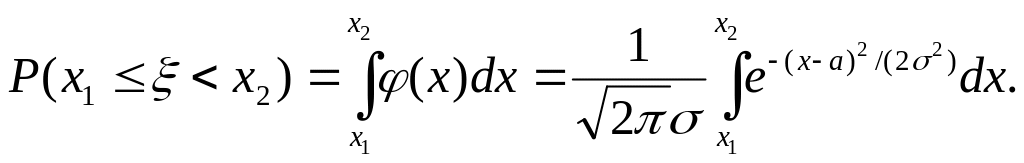
Сделаем в этом интеграле замену переменной, снова полагая (x – a)/σ = t. Тогда x = a+ σt, dx = σdt и

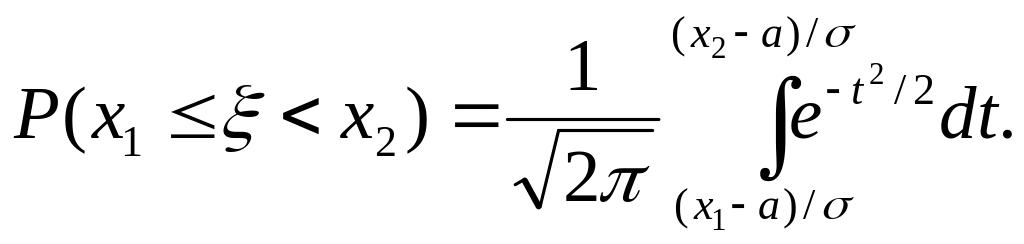(30)

Интеграл не берется в элементарных функциях, поэтому для вычисления определенного интеграла (30) введена функция

(31)

называемая интегралом вероятностей. Для этой функции составлены таблицы ее значений для различных значений аргумента (см. табл. 2 Приложения). Используя формулу (31), получим

То есть

(32)

Легко показать, что функция Ф(x) (интеграл вероятностей) o6ладает следующими свойствами:

1°). Ф(0) = 0.

2°). при |x|≥4 величина |Ф(x)| практически равна 1/2. (см. табл. 2 Приложения).

3°). Ф(–х) = – Ф(х), т. е. интеграл вероятностей является нечетной функцией.

График функции Ф (х) изображен на рис. 12.

Т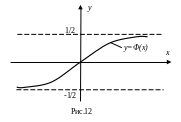 аким образом, если случайная величина ξ нормально распределена с параметрами a и σ, то вероятность того, что случайная величина удовлетворяет неравенствам х₁<ξ<х₂, определяется соотношением (32).

Пусть ε>0. Найдем вероятность того, что нормально распределенная случайная величина ξ отклонится от параметра а по абсолютной величине не более, чем на ε, т. е. P(|ξ – а|< ε).

Так как неравенство |ξ – а|< ε равносильно неравенствам а – ε < ξ < а + ε, то полагая в соотношении (32) х₁ = а – ε, х₂ = а + ε, получим

Вследствие того, что интеграл вероятностей – нечетная функция, имеем Ф(–ε/σ) = = Ф(–ε/σ). Следовательно,

P(|ξ – а|< ε) = 2Ф(ε/σ). (33)

Пример 1. Пусть случайная величина ξ подчиняется нормальному закону распределения вероятностей с параметрами а = 0, σ = 2. Определить: 1). Р(–2< ξ <3); 2). Р(|ξ| < 0,1).

Решение. 1). Используя формулу (32), имеем:

По таблице II Приложения находим Ф (1,5) = 0,43319, Ф(1) = 0,34134. Следовательно, Р(–2< ξ <3) = 0,43319 – 0,34134 = 0,77453.

2). Так как а = 0, то |ξ| = | ξ – а |. По формуле (33) находим

Р(|ξ| < 0,1) = 2∙Ф(0,1/2) = 2∙Ф (0,05) = 2∙0,01994 = 0,03988.

Пример 2. В каких пределах должна изменяться случайная величина, подчиняющаяся нормальному закону распределения, чтобы Р(|ξ – а| < ε) = 0,99730?

Решение. По формуле (33) имеем

Р(|ξ – а| < ε) = 2∙Ф(ε/σ) = 0,99730.

Следовательно, Ф(ε/σ) = 0,49865. Из табл. II находим, что этому значению Ф(ε/σ) соответствует ε/σ = 3, откуда ε = 3σ.

Из последнего примера следует, что если случайная величина подчиняется нормальному закону распределения, то можно утверждать с вероятностью, равной 0,9973, что случайная величина находится в интервале [а – Зσ,, а + Зσ]. Так как данная вероятность близка к единице, то можно считать, что значения нормально распределенной случайной величины практически не выходят за границы интервала [а – Зσ,, а + Зσ]. Этот факт называют правилом трех сигм.

6. Двумерные случайные величины. Часто приходится решать задачи, в которых рассматриваются события, описываемые не одной, а несколькими – в частности, двумя случайными величинами. Так, если станок-автомат штампует цилиндрические валики, то диаметр валика ξ₁ и его длина ξ₂ образуют систему двух случайных величин (ξ₁, ξ₂).

Двумерной случайной величиной называют систему из двух случайных величин (ξ₁, ξ₂), для которой определена вероятность P[(ξ₁<х), (ξ₂<y)] совместного выполнения неравенств ξ₁<х, ξ₂<y, где x и y – любые действительные числа.

Функция двух переменных

F(x,y) = P[(ξ₁<х), (ξ₂<y)],

определенная для любых х и у, называется функцией распределения системы двух случайных величин (ξ₁, ξ₂).

Е сли рассматривать ξ₁, и ξ₂ как декартовы координаты точки М(ξ₁, ξ₂) на плоскости Оξ₁ξ₂, то функция распределения даст вероятность того, что случайная точка М(ξ₁, ξ₂) попадает в область σ, изображенную на рис. 13.

Двумерная случайная величина (ξ₁, ξ₂) называется дискретной, если ξ₁ и ξ₂ – дискретные величины.

Пусть возможные значения ξ₁ и ξ₂ образуют, например, конечные последовательности x₁, x₂,…, x_n и y₁, y₂, … y_m. Возможные значения двумерной случайной величины (ξ₁, ξ₂) имеют вид (х_i„ у_j), где i = 1, 2, …, п, j = 1, 2, …, m. Обозначим через p_ij вероятность того, что (ξ₁, ξ₂) = (x_i, y_j):

p_ij = P[(ξ₁,= x_i), (ξ₂ = y_j)].

Функция распределения F(х, у) имеет вид:

где двойная сумма распространена на те i и j, для которых x_i,<x и y_j<y.

Двумерную случайную величину (ξ₁, ξ₂) так же, как и одномерную, можно задавать таблицей. Первая строка таблицы содержит возможные значения случайной величины ξ₁, а первый столбец возможные значения ξ₂. В остальных клетках таблицы указаны coответствующие вероятности, причем их сумма всегда равна единице. В качестве примера рассмотрим двумерную случайную величину, заданную следующей таблицей:

ξ1 \ ξ2)	–1	0	1
0,1	p11= 0,05	p12= 0,20	p13= 0,30
0,2	p21= 0,10	p22= 0,20	p231= 0,15

Сумма всех вероятностей

Две дискретные случайные величины ξ₁ и ξ₂ называются независимыми, если для всех пар i, j выполняется соотношение:

p_ij = P[(ξ₁,= x_i), (ξ₂ = y_j)] = P(ξ₁,= x_i)∙P(ξ₂ = y_j).

Пример 1. Две игральные кости бросают по одному разу. Обозначим через ξ₁ число очков, выпавшее на первой кости, а через ξ₂ – на второй, тогда (ξ₁, ξ₂) – двумерная дискретная величина. Покажем, что величины ξ₁ и ξ₂ независимы. Так как каждая из величин ξ₁ и ξ₂ независимо друг от друга может принимать 6 различных значений, то число различных значений двумерной случайной величины (ξ₁, ξ₂) равно 36. Все эти значения, очевидно, равновероятны. Поэтому

P[(ξ₁,= x_i), (ξ₂ = y_j)] = 1/36.

С другой стороны, P(ξ₁,= x_i) = 1/6 и P(ξ₂ = y_j) = 1/6. Таким образом

P[(ξ₁,= x_i), (ξ₂ = y_j)] = P(ξ₁,= x_i)∙P(ξ₂ = y_j) = 1/36.

Двумерная величина (ξ₁, ξ₂) называется непрерывной, если существует такая непрерывная неотрицательная функция (х, y) двух переменных, что вероятность того, что точка М(ξ₁, ξ₂) содержится в некоторой области σ плоскости Оξ₁ξ₂, равна двойному интегралу функции (х, y) по области σ.

(35)

Функция (х, y) называется плотностью распределения вероятностей системы двух величин ξ₁ и ξ₂. Отсюда, в частности, следует, что если область σ имеет вид, изображенный на рис. 94, то функцию распределения системы случайных величин можно записать следующим образом:

(36)

Непрерывные случайные величины ξ₁ и ξ₂ называются независимыми, если (х, y) = ₁(х)∙₂(y), где ₁(х) и ₂(y) – соответственно плотности распределения вероятностей случайных величин ξ₁ и ξ₂. В этом случае

где F₁(x) и F₂ (у) – соответственно функции распределения величин ξ₁ и ξ₂. [см. формулу (22)]. Зная функцию распределения F(х, у) двумерной случайной величины (ξ₁, ξ₂), легко найти как функцию распределения, так и плотность распределения каждой из случайных величин ξ₁ и ξ₂ в отдельности.

Действительно, пусть F_l(x) – функция распределения случайной величины ξ₁. Тогда F_l(x) = P(ξ₁<x). Так как в этом случае ξ₂ может принимать любое значение, то ясно, что

P(ξ₁<x) = P[(ξ₁<x), (–∞<ξ₂<+∞)].

Следовательно, по формуле (36) имеем:

Дифференцируя последнее равенство по х, согласно правилу дифференцирования интеграла по переменной верхней границе получим¹⁰

(37)

Аналогичным образом получаем

и, следовательно,

(38)

Т аким образом, чтобы получить плотность распределения одной из составляющих двумерной случайной величины, надо проинтегрировать в границах от –∞ до +∞ плотность распределения системы (х, y) по переменной, соответствующей другой случайной величине.

Пример 2. Двумерная случайная величина (ξ₁, ξ₂) имеет плотность распределения (х, y) = 1/[π²(1 + x²)(1 + y²)]. Найти: 1) вероятность p попадания случайной точки М(ξ₁, ξ₂) в квадрат, изображенный на рис. 14; 2) функцию распределения F(х, у); 3) плотности распределения каждой величины ξ₁ и ξ₂ в отдельности.

Решение.1). Вероятность р попадания случайной точки М(ξ₁, ξ₂) в квадрат, изображенный на рис. 14, согласно формуле (35), равна

2). Используя соотношение (36), находим функцию распределения F(x, y):

3). Плотность распределения случайной величины ξ₁ находим по формуле (37):

Аналогичным образом, используя формулу (38), получим

Легко убедиться в том, что случайные величины ξ₁ и ξ₂ независимы, так как φ(x, y) = φ₁(x)∙φ₂(y)

По определению двумерная случайная величина (ξ₁, ξ₂) распределена нормально, если плотность распределения системы величин ξ₁ и ξ₂ имеет вид:

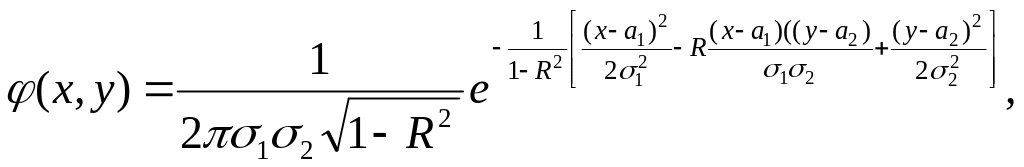
где σ₁>0, σ₂>0, a R – некоторая постоянная (см. §9, п.2). Можно показать [используя формулы (37) и (38)], что каждая из величин ξ₁ и ξ₂ распределена нормально:

На доказательстве этого факта мы не будем останавливаться. В частности, если ξ₁ и ξ₂ независимы, то (х, y)= ₁(хy)∙₂(y). Отсюда следует, что R = 0, и, следовательно,

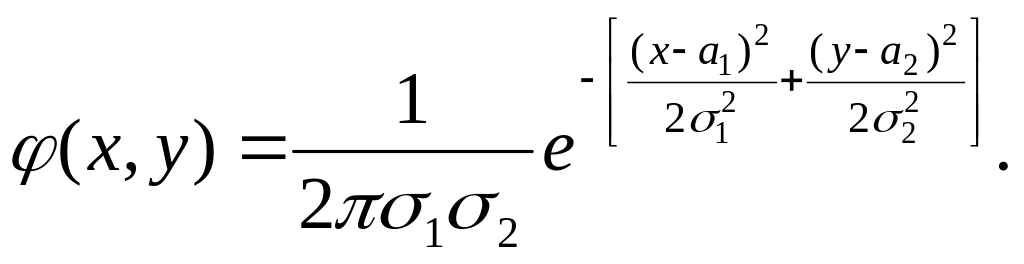
Нетрудно убедиться в том, что справедливо и обратное утверждение: если R= 0, то ξ₁ и ξ₂ – независимые случайные величины.