§ 5. Законы больших чисел

1. Леммы Чебышева. В этом пункте приводится доказательство двух лемм, принадлежащих Чебышеву¹⁵.

Лемма 1. Для случайной величины η, принимающей только неотрицательные значения, справедливо неравенство Р(η ≥ 1) ≤ М(η).

Доказательство. Для простоты приводится доказательство этого утверждения для дискретной случайной величины η, принимающей значения х_1, х₂, ..., х_п, при условии x_i ≥ 0, По аксиоме сложения вероятностей имеем

где суммирование распространено на все значения х_i, большие или равные единице. Но для, очевидно, Р(η = x_i) ≤ x_iР(η = x_i). Поэтому

(50)

Добавим к правой части неравенства (50) сумму , где x_i < 1. Эта сумма неотрицательна, так как все x_i ≥ 0 по условию, вероятности Р(η = x_i) ≥ 0. Поэтому

(51)

Последняя сумма распространена на все значения x_i, принимаемые случайной величиной η. Но эта сумма по определению равна математическому ожиданию: Сопоставляя уравнения (50) и (51) имеем

Лемма доказана.

Лемма 2. Для случайной величины ξ и любого положительного числа ε вероятность того, что модуль отклонения случайной величины от ее математического ожидания окажется меньше, чем ε, больше или равна разности 1 – D(ξ)/ε², т. е.

(52)

Неравенство (52) называется неравенством Чебышева.

Доказательство. Рассмотрим сначала неравенство | – М()| ≥ ε. Так как оно равносильно неравенству , то

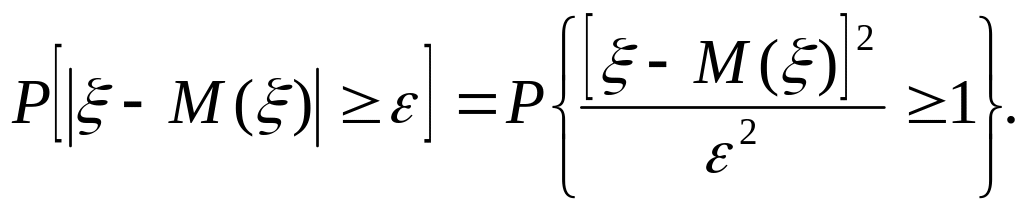
Случайная величина неотрицательна и, значит, удовлетворяет условиям первой леммы Чебышева. Следовательно,

так как M[ – M()]² = D(). Поэтому

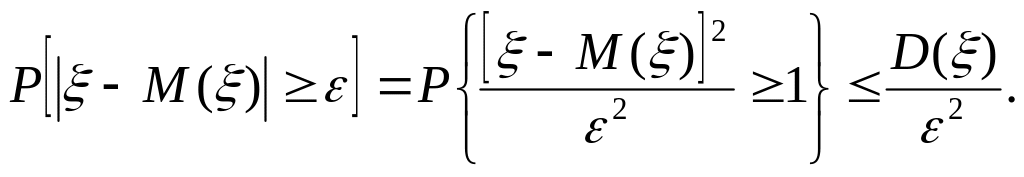(53)

Так как событие, выражаемое неравенством | – М()| < ε, противоположно событию, выражаемому неравенством | – М()| ≥ ε, то P[| – М()| < ε] = 1 – P[| – М()| ≥ ε]. Принимая во внимание соотношение (53), окончательно получим

Лемма доказана.

2. Закон больших чисел Чебышева. Для любой последовательности попарно независимых случайных величин x₁, x₂, … x_n, …, имеющих ограниченные в совокупности дисперсии, т. е. D(x_i) ≤ C для любого i, и для любого ε > 0 справедливо соотношение

(54)

Доказательство. Обозначим через ξ_n величину (ξ₁ + ξ₂ + … + ξ_n)/n, т. е. среднюю арифметическую п случайных величин. Случайная величина ξ_n имеет математическое ожидание

и дисперсию

(здесь используются свойства математического ожидания и дисперсии). Применяя к случайной величине ξ_n = (ξ₁ + ξ₂ + … + ξ_n)/n вторую лемму Чебышева, найдем, что

т.е.

так как D(x_i) ≤ C при любом i и, следовательно, D(ξ₁) + D(ξ₂) + … + D(ξ_n) ≤ nC. Учитывая, что вероятность любого события не превосходит единицы, получим

Переходя к пределу при п  ∞, имеем

Смысл закона больших чисел Чебышева состоит в следующем. В то время как отдельная случайная величина может принимать значения, очень далекие от своего математического ожидания, средняя арифметическая большого числа случайных величин с вероятностью, близкой к единице, принимает значение, мало отличающееся от среднего арифметического их математических ожиданий.

Частный случай закона больших чисел Чебышева. Для любой последовательности попарно независимых случайных величин x₁, x₂, … x_n, …, имеющих ограниченные в совокупности дисперсии (D(x_i) ≤ C) и одинаковые математические ожидания М(_i) = a и для любого ε > 0 справедливо соотношение:

Это непосредственно следует из формулы (54), так как

Замечание. Говорят, что случайная величина ξ_n сходится по вероятности к числу А, если при сколь угодно малом ε > 0 вероятность неравенства |_n A| < ε с увеличением п неограниченно приближается к единице. Сходимость по вероятности не означает, что . Действительно, в последнем случае неравенство |_n A|< ε выполняется для всех достаточно больших значений п. В случае же сходимости по вероятности это неравенство для отдельных сколь угодно больших значений п может не выполняться. Однако невыполнение неравенства |_n A| < ε для больших значений п есть событие очень редкое (маловероятное). Принимая это во внимание, частный случай закона больших чисел Чебышева можно сформулировать так:

Средняя арифметическая (ξ₁ + ξ₂ + … + ξ_n)/n попарно независимых случайных величин x₁, x₂, … x_n, имеющих ограниченные в совокупности дисперсии и одинаковые математические ожидания М(_i) = a, сходится по вероятности к а.

Поясним смысл частного случая закона больших чисел Чебышева. Пусть требуется найти истинное значение а некоторой физической величины (например, размер некоторой детали). Для этого будем производить ряд независимых друг от друга измерений. Всякое измерение сопровождается некоторой погрешностью (см. подробнее §6, п.1). Поэтому каждый возможный результат измерения есть случайная величина _i, (индекс i – номер измерения). Предположим, что в каждом измерении нет систематической ошибки, т. е. отклонения от истинного значения а измеряемой величины в ту и другую стороны равновероятны. В этом случае математические ожидания всех случайных величин _i одинаковы и равны измеряемой величине a, т. е. М(_i) = a.

Предположим, наконец, что измерения производятся с некоторой гарантированной точностью. Это значит, что для всех измерений D(x_i) ≤ C. Таким образом, мы находимся в условиях закона больших чисел Чебышева, а потому, если число измерений достаточно велико, то с практической достоверностью можно утверждать, что каково бы ни было ε > 0, средняя арифметическая результатов измерений отличается от истинного значения а меньше, чем на ε.

3. Закон больших чисел Бернулли. Пусть производится последовательность независимых испытаний, в результате каждого из которых может наступить или не наступить событие А, причем вероятность наступления этого события одна и та же при каждом испытании и равна р. Если событие А фактически произошло т раз в n испытаниях, то отношение m/n называют, как мы знаем, частотой появления события А. Частота есть случайная величина, причем вероятность того, что частота принимает значение m/n, выражается по формуле Бернулли (13): .

Закон больших чисел в форме Бернулли состоит в следующем: с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе опытов частота появления события А как угодно мало отличается от его вероятности, т. е.

(55)

каково бы ни было положительное число ε.

Иными словами, при неограниченном увеличении числа п опытов частота т/п события А сходится по вероятности к Р(А).

Доказательство. Рассмотрим случайную величину ξ = m/n. Так как М(т)=пр и D(m) = npq (см. §4, п.2, пример 3), то

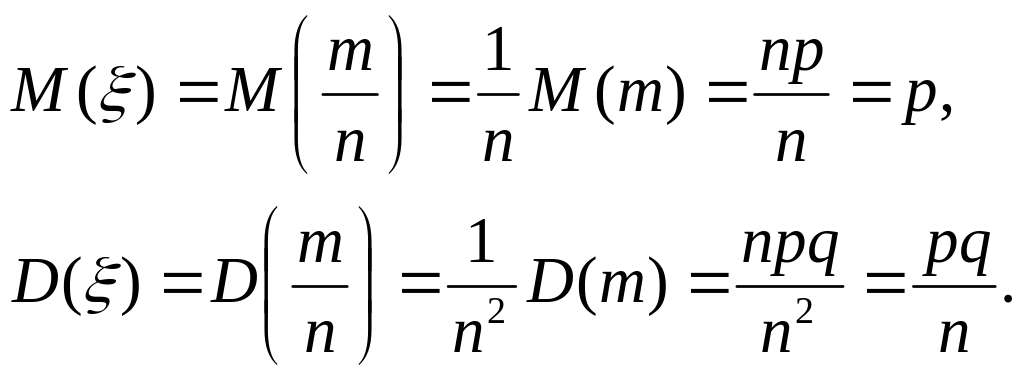
Применим к случайной величине ξ вторую лемму Чебышева:

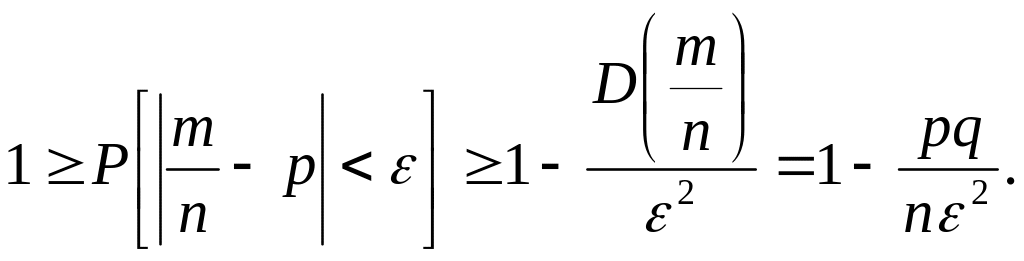
Переходя к пределу при п  ∞, очевидно, имеем

Ранее было сказано (см. §1, п.1), что при большом числе испытаний частота P*(A)= = m/n события А обладает свойством устойчивости. Это обстоятельство находит свое объяснение в законе больших чисел Бернулли.