Применение теории вероятностей к статистике

Математическая статистика – это раздел математики, в котором изучаются методы обработки и анализа экспериментальных данных, полученных в результате наблюдений над массовыми случайными явлениями. Таким образом, обработка результатов измерения (см. §7) является одной из задач математической статистики. В этом параграфе мы рассмотрим еще две задачи математической статистики.

1. Определение неизвестной функции распределения. Пусть мы имеем дело с непрерывной случайной величиной ξ, значения которой получены из наблюдений. Разобьем диапазон наблюдаемых значений ξ на интервалы ]Х₀; Х₁[, ]Х₁; Х₂[, ..., ]X_k-_l; X_k[ одинаковой длины ΔХ. Ориентировочно количество интервалов можно определить по формуле

k = ln(n). (64)

Пусть m_i – число наблюдаемых значений ξ, попавших в i-й интервал. Разделив m_i на общее число наблюдений п, получим частоту p_i*, соответствующую i-му интервалу: р_i* = т_i/п, причем Составим следующую таблицу:

Номер интервала	Интервал	mi	pi*
1	]Х0; Х1[	m1	p1*
2	]Х1; Х2[	m2	p2*
…	…	…	…
k	]Xk-l; Xk[	mk	pk*

которая называется статистическим рядом. Эмпирической (или статистической) функцией распределения случайной величины ξ называется частота события, заключающегося в том, что величина в результате опыта примет значение, меньшее х:

F*(x) = P*(ξ<x).

На практике достаточно найти значения статистической функции распределения F*(x) в точках Х₀, Х₁, …, X_k, которые являются границами интервалов статистического ряда:

(65)

С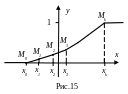 ледует заметить, что F*(х) = 0 при х < Х_о и F*(х) = 1 при х > X_k. Построив точки M_i[X_i, F*(X_i)] и, соединив их плавной кривой, получим приближенный график эмпирической функции распределения (рис. 15). Используя закон больших чисел Бернулли, можно доказать, что при достаточно большом числе п испытаний с вероятностью, близкой к единице, эмпирическая функция распределения F*(х) отличается сколь угодно мало от неизвестной нам функции распределения F(х) случайной величины ξ.

Ч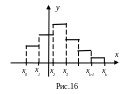 асто вместо построения графика эмпирической функции распределения поступают следующим образом. На оси абсцисс откладывают интервалы ]Х₀, Х₁[, ]Х₁, Х₂[, ]X_k-1, X_k[. На каждом интервале строят прямоугольник, площадь которого равна частоте p_i*, соответствующей данному интервалу. Высота h_i этого прямоугольника равна h_i = =p_i*/ΔX, где ΔХ – длина каждого из интервалов. Ясно, что сумма площадей всех построенных прямоугольников равна единице.

Рассмотрим функцию у = φ*(х), которая в интервале ]Х_i-1, X_i[ постоянна и равна h_i. График этой функции называется гистограммой. Он представляет собой ступенчатую линию (рис. 16). С помощью закона больших чисел Бернулли можно доказать, что при малых ΔХ и больших n с практической достоверностью функция φ*(х) как угодно мало отличается от плотности распределения φ(x) непрерывной случайной величины ξ.

Пример. Измерен диаметр у 270 валов хвостовика. Значения диаметра (в см) оказались в диапазоне 66—90 см. Разбив этот диапазон на интервалы длиной 2 см (ΔX = 2), получим статистический ряд (см. таблицу):

Номера интервалов	Интервалы	mi	рi* = тi/п	hi = pi*/ΔX
(1)	(2)	(3)	(4)	(5)
1 2 3 4 5 6 7 8 9 10 11 12	]66,68[ ]68,70[ ]70,72[ ]72,74[ ]74,76[ ]76,78[ ]78,80[ ]80,82[ ]82,84[ ]84,86[ ]86,88[ ]88,90[	4 12 24 41 50 53 39 26 13 5 2 1	0,015 0,045 0,090 0,152 0,185 0,196 0,144 0,096 0,048 0,019 0,007 0,003	0,008 0,022 0,045 0,076 0,092 0,098 0,072 0,048 0,024 0,009 0,004 0,002
∑		270	1,000

Построим гистограмму и эмпирическую функцию распределения. Рассчитанные частоты р_i* приведены в столбце (4), а значения высот h_i прямоугольников гистограммы – в столбце (5). Гистограмма изображена на рис. 17. Значения эмпирической функции распределения в граничных точках интервалов вычислены по формулам (65) и приведены в следующей таблице.

x	66	68	70	72	74	76	78	80	82	84	86	88	90
F*(x)	0	0,015	0,060	0,150	0,302	0,487	0,683	0,827	0,923	0,971	0,990	0,997	1,000

Так, например,

Г рафик функции F* (х) изображен на рис. 18.

2. Определение неизвестных параметров распределения. С помощью гистограммы мы можем приближенно построить график плотности распределения случайной величины ξ. Вид этого графика часто позволяет высказать предположение о плотности распределения вероятностей (x) случайной величины ξ. В выражение этой плотности распределения обычно входят некоторые параметры, которые требуется определить из опытных данных. Остановимся на том частном случае, когда плотность распределения (x) зависит от двух параметров.

Итак, пусть х₁, х₂, ..., х_п – наблюдаемые значения непрерывной случайной величины ξ, и пусть ее плотность распределения вероятностей зависит от двух неизвестных параметров А и В, т. е. имеет вид (x, А, В). Один из методов нахождения неизвестных параметров А и В состоит в том, что их выбирают таким образом, чтобы математическое ожидание и дисперсия теоретического распределения совпали с выборочными средним значением и дисперсией .

, , (66)

где

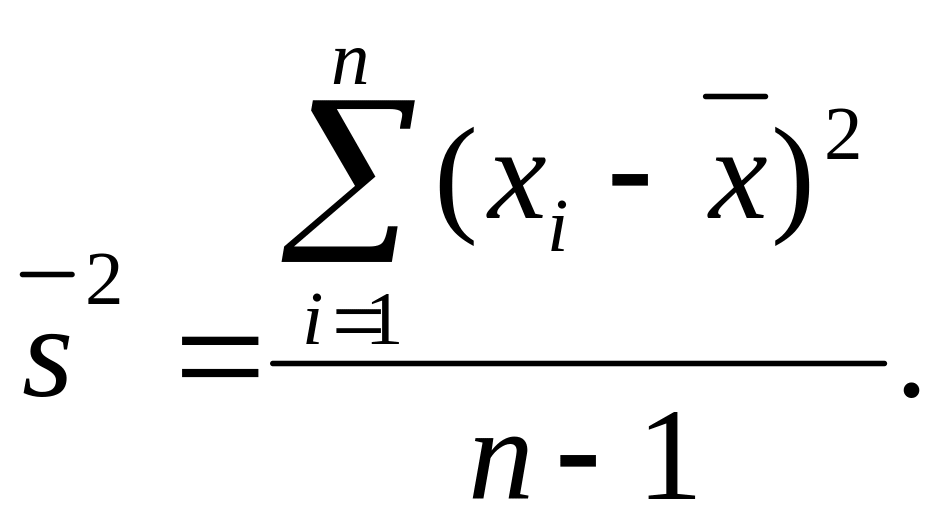(67)

Из двух полученных уравнений (66) находят неизвестные параметра А и В. Так, например, если случайная величина ξ подчиняется нормальному закону распределения вероятностей, то ее плотность распределения вероятностей зависит от двух параметров а и σ. Эти параметры, как мы знаем, являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины ξ; поэтому равенства (66) запишутся так

. (68)

Следовательно, плотность распределения вероятностей имеет вид

Замечание 1. Такая задача уже решалась в предыдущем разделе применения теории вероятности к обработке результатов измерений. Результат измерения есть случайная величина ξ, подчиняющаяся нормальному закону распределения с параметрами а и σ. За приближенное значение а была выбрана величина , а за приближенное значение σ – величину .

Замечание 2. При большом количестве опытов нахождение величин и по формулам (67) связано с громоздкими вычислениями. Поэтому поступают так: каждое из наблюдаемых значений величины ξ, попавшее в i-й интервал ]X_i-1, X_i[ статистического ряда, считают приближенно равным середине c_i этого интервала, т. е. c_i = (X_i-1, – X_i)/2. Рассмотрим первый интервал ]Х₀, Х₁[. В него попало m₁ наблюдаемых значений случайной величины ξ, каждое из которых мы заменяем числом с₁. Следовательно, сумма этих значений приближенно равна m₁∙c_l. Аналогично, сумма значений ξ, попавших во второй интервал, приближенно равна m₂∙c₂ и т. д. Поэтому

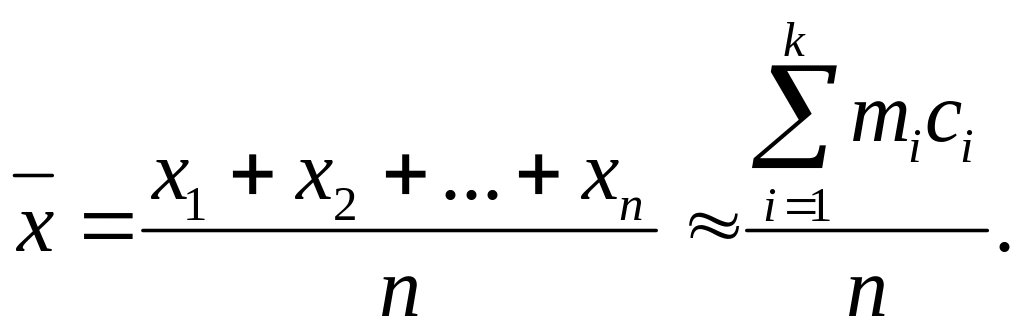
Подобным же образом получим приближенное равенство

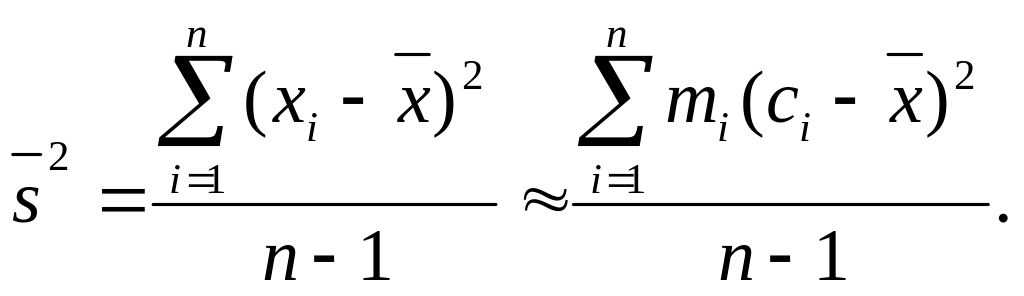
Итак,

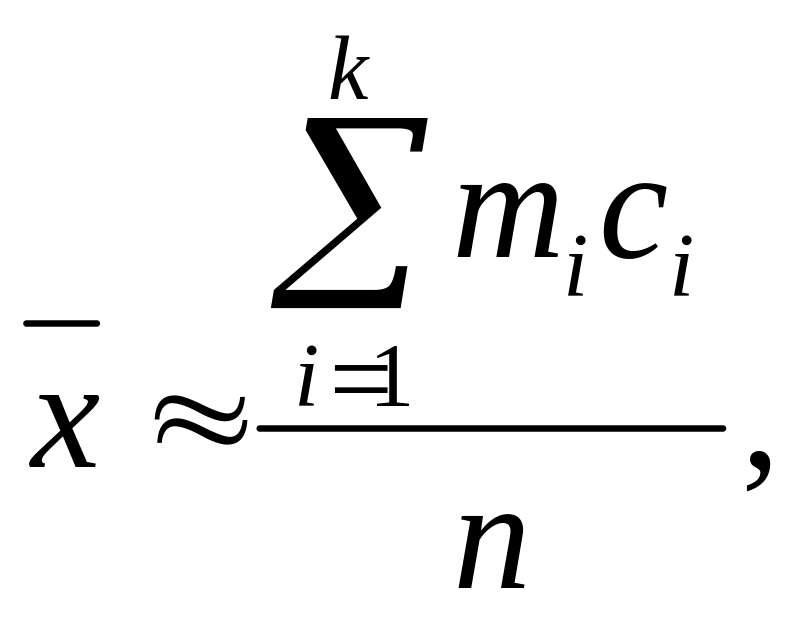
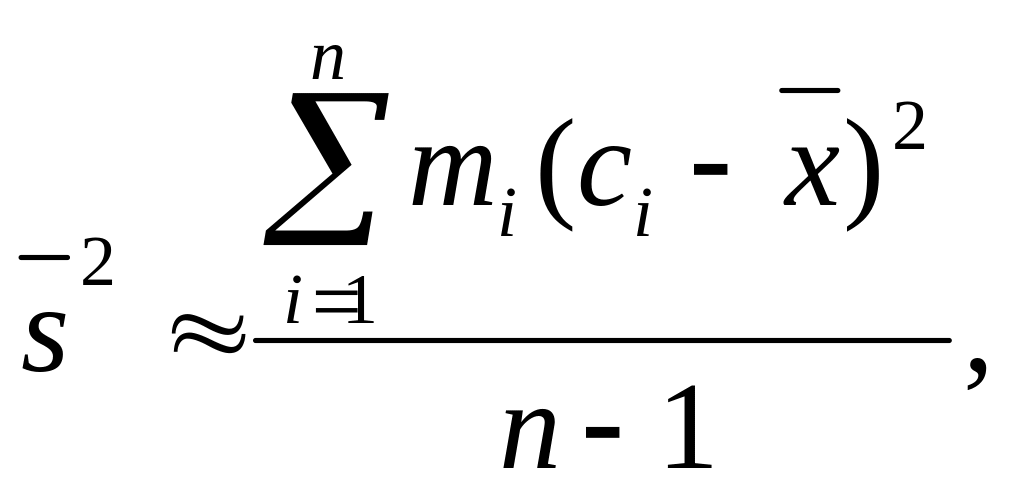(69)

где n = m₁-+-m₂ + ... + m_k, a k – число интервалов статистического ряда.

Замечание 3. На практике для еще большего упрощения вычислений прибегают к следующему приему. Пусть х₀ – произвольное число. Обозначим u_i = c_i – x₀. и рассмотрим величины v₁ и v₂, определяемые соотношениями

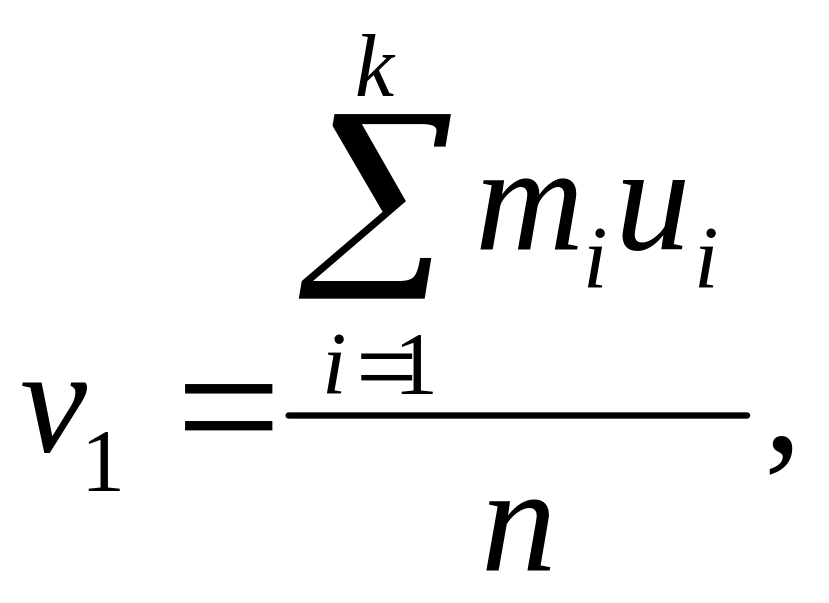
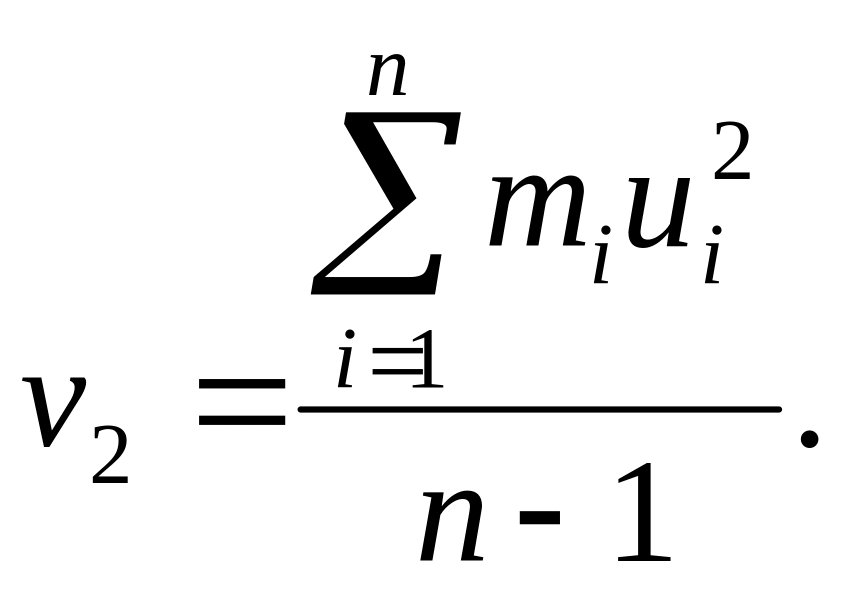(70)

Покажем, что

(71)

Действительно,

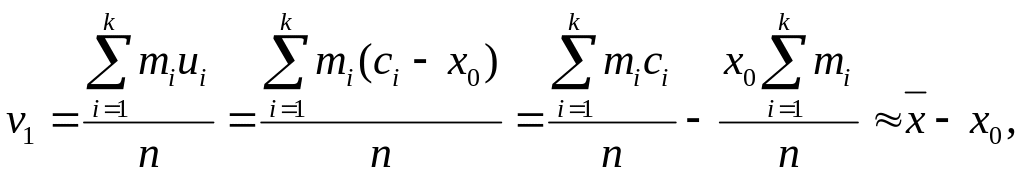
так как а 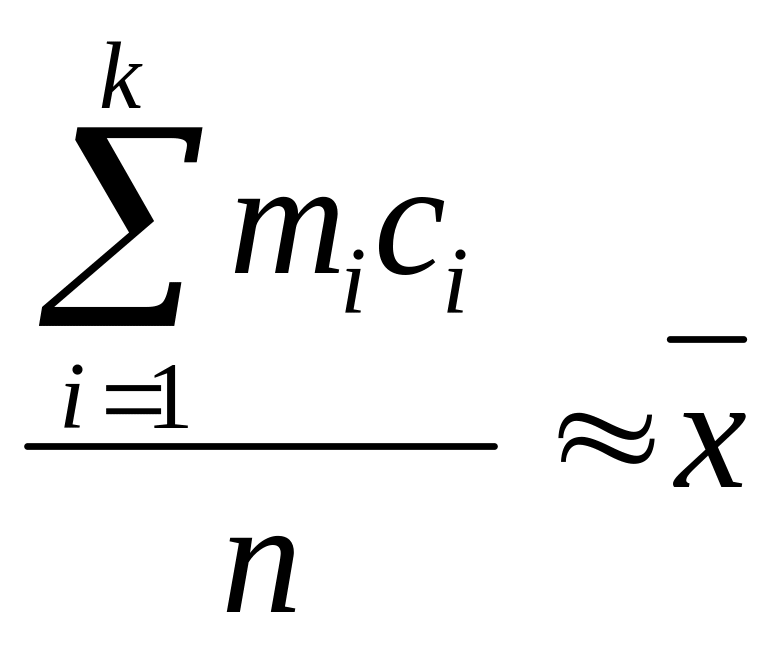[см. формулы (69)]. Итак, откуда Аналогично доказывается и второе из соотношений (71).

Пример. Построенная гистограмма для статистического распределения значений диаметра хвостовика вала (см. рис. 98) позволяет сделать предположение о том, что мы имеем дело с нормальным законом распределения. Требуется, исходя из опытных данных, представленных в табл. на с. 40, определить параметры a и σ этого распределения.

Решение. Полагая¹⁸ x₀ = 75, вычислим v₁ и v₂. Вычисления расположим, как указано в следующей таблице.

Номер интервала	Середина интервала ci	mi	ui = ci - 75	mi ui	ui2	mi ui2
1	67	4	-8	-32	64	256
2	69	12	-6	-72	36	432
3	71	24	-4	-96	16	384
4	73	41	-2	-82	4	164
5	75	50	0	0	0	0
6	77	53	2	106	4	212
7	79	39	4	156	16	624
8	81	26	6	156	35	936
9	83	13	8	104	54	832
10	85	5	10	50	100	500
11	87	2	12	24	144	288
12	89	1	14	14	196	196
∑		270		328		4824

По формулам (70) находим

Используя теперь формулы (71), имеем

Выберем параметры a и σ так, чтобы выполнялись условия (68): Следовательно, Таким образом, плотность распределения вероятностей

В следующей таблице приведены вычисления значений функции φ(х) в средних точках интервала статистического ряда. Значения функции взяты из табл. I Приложения.

x	x – 76,21		φo(t)		φ*(x) = hi
67	– 9,21	– 2,27	0,0303	0,006	0,008
69	– 7,21	– 1,78	0,0818	0.020	0,022
71	– 5,21	– 1,29	0,1736	0.043	0,045
73	– 3,21	– 0,79	0,2920	0,072	0,076
75	– 1,21	– 0,30	0,3697	0,091	0,092
77	0,79	0,20	0,3825	0,095	0,098
79	2,79	0,69	0,3144	0,075	0.072
81	4,79	1,18	0,1989	0,049	0,048
83	6,79	1,62	0.0973	0,024	0,024
85	8,79	2,17	0,0379	0,009	0,009
87	10,79	2,66	0,0116	0,003	0,004
89	12,79	3,16	0,0020	0,001	0,002

В последнем столбце таблицы приведены значения функции φ*(х), взятые из 5-го столбца предыдущей таблицы. Сравнение показывает, что функция φ(x) близка к φ*(х).