Приложение теории вероятностей к обработке результатов измерений
Пусть для определения неизвестной физической постоянной а производится п независимых измерений, причем считается, что грубые и систематические ошибки отсутствуют (см. §6, п.2 раздела теории вероятностей). Возможный результат каждого из п измерений есть случайная величина, которую мы обозначим через ξi (i – номер измерения). Так как каждое измерение не зависит от результатов других измерений, то мы имеем п случайных независимых величин x1, x2, … xn. Обозначив через х1, х2, ..., хп фактически полученные результаты п измерений величины а. Таким образом, xi есть одно из возможных значений ξi.
На основании закона больших чисел Чебышева (см. §5, п.2) можно утверждать, что с практической достоверностью для достаточно большого числа п измерений средняя арифметическая результатов измерений отличается от истинного значения физической постоянной сколь угодно мало, т. е. с вероятностью, сколь угодно близкой к единице, имеет место приближенное равенство
Оценим точность этого приближенного равенства. Для этого, прежде всего, заметим, что в силу основного закона ошибок (см §6, п.2 раздела теории вероятностей) каждый возможный результат измерения ξi есть случайная величина, подчиняющаяся нормальному закону распределения вероятностей с одним и тем же математическим ожиданием, равным истинному значению а измеряемой величины: M(ξi) = a (i = l, 2, … n). Далее будем предполагать, что все измерения проводятся с одинаковой степенью точности (равноточные измерения). Поэтому дисперсии всех случайных величин должны быть одинаковыми, т. е. D(ξi) = σ2.
Сначала
рассмотрим случай оценки неизвестного
значения а,
предполагая
известным значение σ.
Так как возможный результат i-го
измерения есть случайная величина ξi,
подчиняющаяся нормальному закону
распределения вероятностей с математическим
ожиданием M(ξi)
= a
и дисперсией D(ξi)
= σ2,
то случайная величина
= (ξ1
+ ξ2
+ … + ξn)/n
также имеет нормальное распределение
с тем же математическим ожиданием M(
)
= a
и средним квадратическим отклонением
(см. §4, п.3 раздела теории вероятностей).
Поэтому плотность распределения
вероятностей для средней арифметической
имеет вид
где
параметры распределения равны а
и
Следовательно, вероятность того, что при п измерениях мы получим такую совокупность значений x1, x2, … xn, что при любом ε > 0 интервал ] –ε, +ε[ будет содержать а, на основании формулы (33) определяется соотношением
(58)
Интервал
]
–ε,
+ε[
имеет случайные границы
–ε
и
+ε.
Соотношение (58) справедливо для любого
значения n
≥ 1. Вероятность
не
зависит от конкретных значений, которые
принимают случайные величины x1,
x2,
… xn,
и, при возрастании числа измерений п,
в
силу свойства функции Ф(x),
возрастает (см. §3, п.4). Соотношение (58)
показывает, что каковы бы ни были значения
x1,
x2,
… xn,
полученные при измерении, имеет место
формула
(59)
где
.
Величина
называется
средней
выборочной.
Формулой
(59) в большинстве случаев пользоваться
нельзя, так как обычно значение σ
неизвестно. Поэтому рассмотрим случай,
когда обе величины а
и σ
неизвестны.
Введём случайную величину s2, определенную соотношением
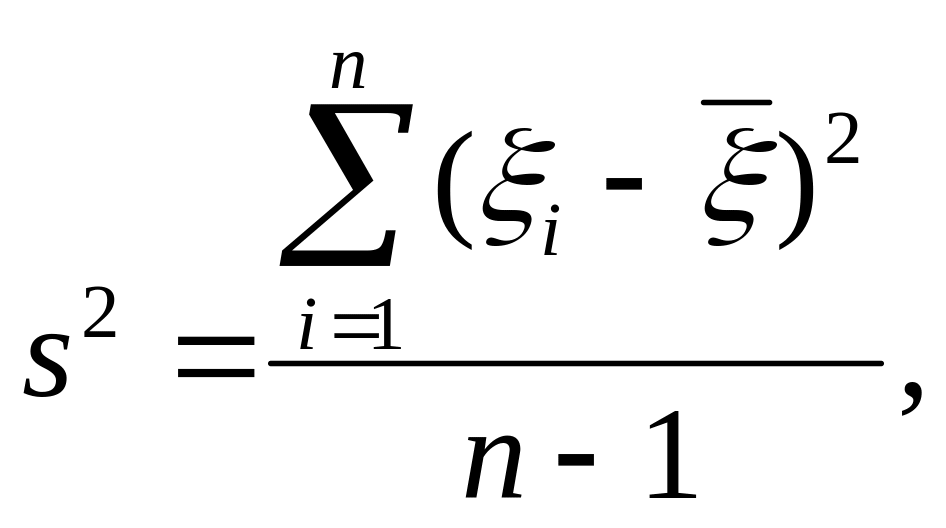(60)
где
= (ξ1
+ ξ2
+ … + ξn)/n.
Можно показать, что величина s2
имеет математическое ожидание, равное
σ2,
и дисперсию, σ
равную
;
т. е. М(s2)
= σ2,
D(s2)
=
(доказательство
не приводится ввиду громоздкости
вычислений). Применим к случайной
величине s2
вторую лемму Чебышева (см. §5, п.1):
где ε > 0. Подставляя значения М(s2) и D(s2), получим
(61)
Соотношение (61) показывает, что если п → ∞, то P[|s2 σ2| < ε] → 1, т. е. s2 стремится по вероятности к σ2.
Рассмотрим
величину
.
Так
как
есть
одно из возможных значений s2,
то при достаточно больших п
с
практической достоверностью можно
утверждать, что имеет место приближение
равенство
или
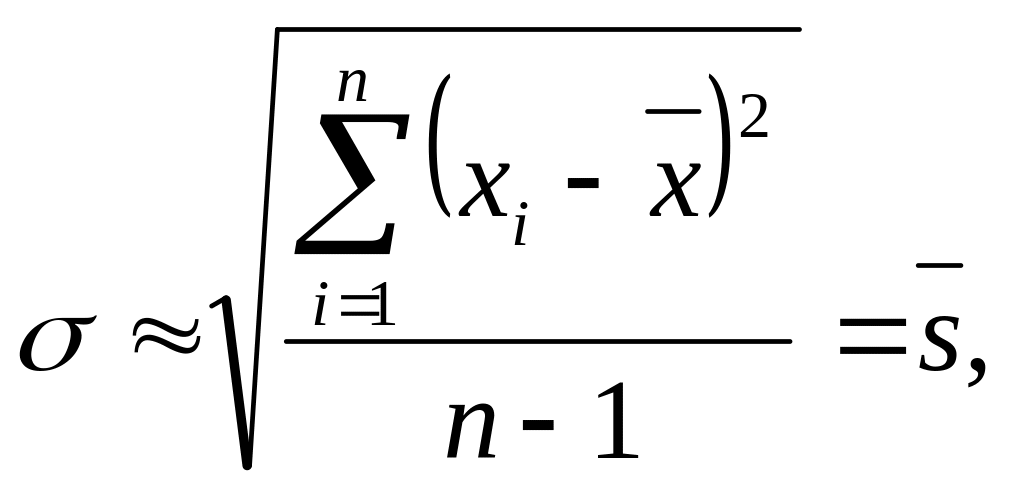(62)
где . Величину называют выборочной дисперсией.
На
практике для оценки вероятности того,
что истинное значение а
измеряемой
величины лежит в интервале ]
–ε,
+ε[,
пользуются формулой (59), где вместо σ
подставляют
ее приближенное значение
,
найденное по формуле (62).
Итак, для достаточно больших значений п имеем
(63)
где
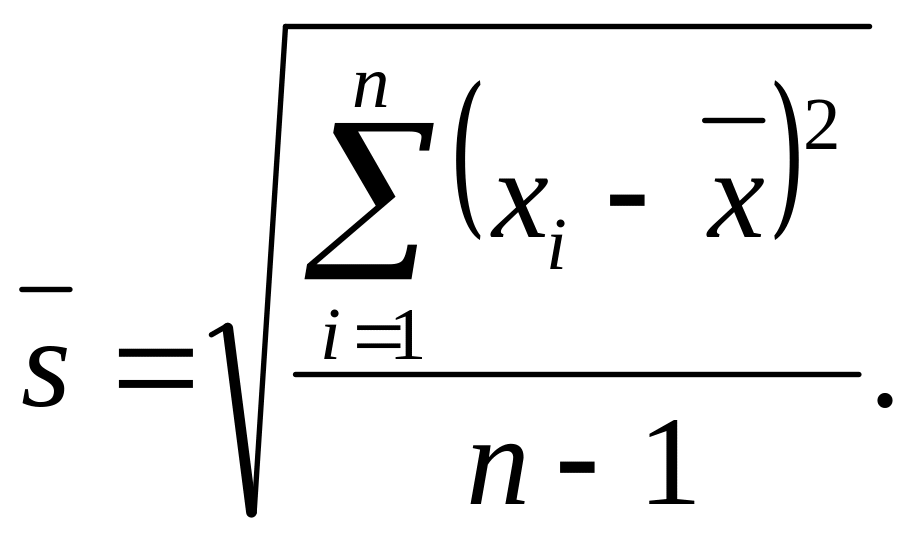(64)
Интервал
]
–ε,
+ε[
называется доверительным
интервалом а
вероятность, вычисленная по формуле
(63)
– надежностью17*.
Пример. Для определения процентного содержания хрома в стали были выполнены 34 измерения, результаты которых сведены в следующую таблицу.
№ |
|
|
|
№ |
|
|
|
1 |
4,505 |
0∙10-3 |
0∙10-6 |
19 |
4,507 |
2∙10-3 |
4∙10-6 |
2 |
4,525 |
19∙10-3 |
361∙10-6 |
20 |
4,502 |
-3∙10-3 |
9∙10-6 |
3 |
4,492 |
-13∙10-3 |
169∙10-6 |
21 |
4,497 |
-8∙10-3 |
64∙10-6 |
4 |
4,500 |
-5∙10-3 |
25∙10-6 |
22 |
4,485 |
-20∙10-3 |
400∙10-6 |
5 |
4,493 |
-12∙10-3 |
144∙10-6 |
23 |
4,511 |
6∙10-3 |
36∙10-6 |
6 |
4,515 |
10∙10-3 |
100∙10-6 |
24 |
4,519 |
14∙10-3 |
196∙10-6 |
7 |
4,504 |
-1∙10-3 |
1∙10-6 |
25 |
4,513 |
8∙10-3 |
64∙10-6 |
8 |
4,508 |
3∙10-3 |
9∙10-6 |
26 |
4,517 |
12∙10-3 |
144∙10-6 |
9 |
4,517 |
12∙10-3 |
144∙10-6 |
27 |
4,508 |
3∙10-3 |
9∙10-6 |
10 |
4,513 |
8∙10-3 |
54∙10-6 |
28 |
4,504 |
-1∙10-3 |
1∙10-6 |
11 |
4,519 |
14∙10-3 |
196∙10-6 |
29 |
4,515 |
10∙10-3 |
100∙10-6 |
12 |
4,511 |
6∙10-3 |
36∙10-6 |
30 |
4,493 |
-12∙10-3 |
144∙10-6 |
13 |
4,485 |
-20∙10-3 |
400∙10-6 |
31 |
4,500 |
-5∙10-3 |
25∙10-6 |
14 |
4,497 |
-8∙10-3 |
64∙10-6 |
32 |
4,492 |
-13∙10-3 |
169∙10-6 |
15 |
4,502 |
-3∙10-3 |
9∙10-6 |
33 |
4,424 |
19∙10-3 |
361∙10-6 |
16 |
4,507 |
2∙10-3 |
4∙10-6 |
34 |
4,505 |
0∙10-3 |
0∙10-6 |
17 |
4,501 |
-4∙10-3 |
16∙10-6 |
∑ |
153,186 |
|
6968∙10-6 |
18 |
4,501 |
-4∙10-3 |
16∙10-6 |
Найти доверительный интервал с надежностью α = 0,9973.
Решение. Здесь n = 34. Используя табличные данные, находим
; 
;
.
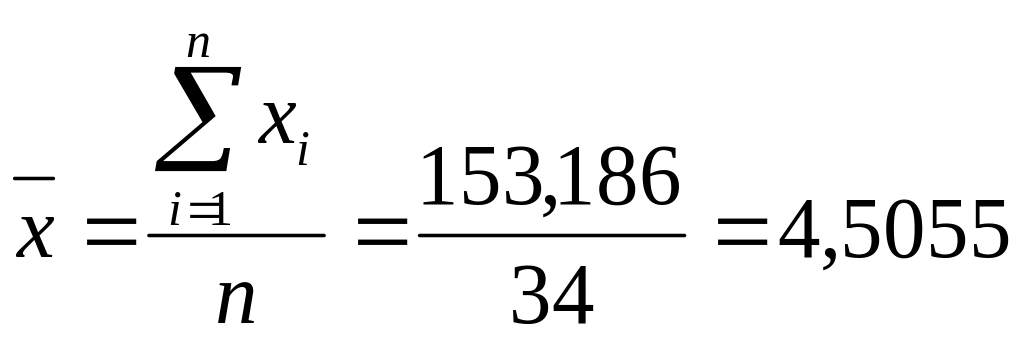При надежности α = 0,9973 по формуле (63) получим
Следовательно, Ф(ε/0,0025) = 0,49865. Из табл.II Приложения найдем ε/0,0025 = 3, откуда получаем ε = 0,0025 ∙ 3 = 0,0075.
В данном случае доверительный интервал ] –ε, +ε[ = ]4,5055 – 0,0075; 4,5055 + 0,0075[ = =]4,498; 4,513[.
Итак, с надежностью α = 0,9973 процентное содержание хрома в стали находится в интервале ]4,498; 4,513[.