Предел функции, правило Лопиталя.

Правило Лопиталя очень широко применяется для вычисления пределов, когда имеет место неопределенность вида ноль делить на ноль , бесконечность делить на бесконечность . К этим видам неопределенностей сводятся неопределенности ноль умножить на бесконечность и бесконечность минус бесконечновть . Дифференцирование функции и нахождение производной является неотъемлемой частью правила Лопиталя, так что рекомендуем обращаться к этому разделу. Формулировка правила Лопиталя cледующая: Если 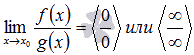, и если функции f(x) и g(x) – дифференцируемы в окрестности точки , то 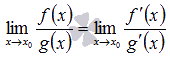В случае, когда неопределенность не исчезает после применения правила Лопиталя, то его можно применять вновь. Рассмотрим несколько примеров и подробно разберем решения. Пример. Вычислить предел, используя правило Лопиталя Решение. Подставляем значение Пределы с неопределенностью данного типа можно находить по правилу Лопиталя: 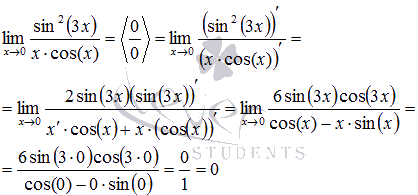Ответ: Пример. Найти предел 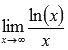Решение. Подставляем бесконечность Для данного типа неопределенностей можно использовать правило Лопиталя при нахождении предела. Ответ:

34)

Общая схема исследования функции и построения ее графика

• Найти область определения функции. Выделить особые точки (точки разрыва).

• Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.

• Найти точки пересечения с осями координат

• Установить, является ли функция чётной или нечётной.

• Определить, является ли функция периодической или нет (только для тригонометрических функций, остальные непериодические, пункт пропускается).

• Найти точки экстремума и интервалы монотонности (возрастания и убывания) функции.

• Найти точки перегиба и интервалы выпуклости-вогнутости.

• Найти наклонные асимптоты функции.

• Построить график функции.

Добавить пример

35) Функция, от которой производная равна данной функции, называется первообразной функцией по отношению к этой данной.

 Рассмотрим функцию   на всей числовой оси    -- на интервале   . Тогда функция    -- это первообразная для   на   .

Для доказательства найдём производную от   :

Поскольку равенство верно при всех   , то    -- первообразная для   на   .     

Аналогичное определение дадим и для случая, когда функция   задана не на одном интервале, а на объединении нескольких непересекающихся интервалов:

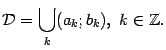
Назовём функцию   первообразной для   , если при всех   выполнено равенство   .

Неопределённый интегра́л для функции   — это совокупность всех первообразных данной функции.

Если функция   определена и непрерывна на промежутке   и   — её первообразная, то есть   при  , то

  ,

где С — произвольная постоянная.

Если  , то и  , где u = φ(x) — произвольная функция, имеющая непрерывную производную

 

 

36) Определение первообразной. Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство для любого х из заданного промежутка. Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.