Точки разрыва

Если попытаться построить отрицание свойства непрерывности функции в точке (предельной для области определения), то получится следующее. Существует такая окрестность значения функции в рассматриваемой точке, что сколь близко мы не подходили бы к данной точке, всегда можно будет найти точку, значение в которой окажется за пределами заданной окрестности.

В этом случае говорят, что функция f терпит разрыв в точке a.

Возможны два варианта:

• либо предел функции существует, но он не совпадает со значением функции в данной точке:

тогда точка a называется точкой устранимого разрыва функции f (в комплексном анализе — устранимая особая точка). Положив   можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.

• либо предела функции в данной точке не существует. В этом случае для числовой функции, заданной на вещественной прямой (или её подмножестве), возможно существование односторонних пределов. Отсюда возникает классификация точек (неустранимого) разрыва:

  • если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;

  • если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

Точка, в которой функция не определена, будет точкой разрыва функции лишь при условии, если функция определена, хотя бы с одной стороны вблизи этой точки.

15) Геометрический и механический смысл производной

Геометрический смысл производной

Пусть функция   определена в некоторой окрестности   токи  , непрерывна в этой точке и  , а   (рис.2).

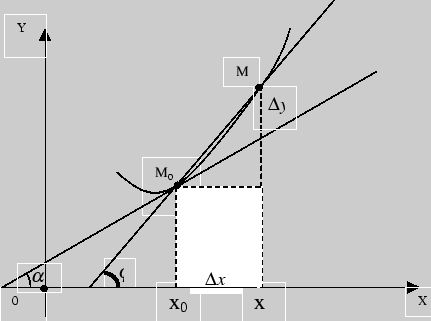
Рис. 2

Придав произвольное приращение аргументу  , так чтобы  , перейдем к точке   с абсциссой   и ординатой  , где  Уравнение прямой, проходящей через точки   и   (секущей графика функции  , имеет вид:  , где отношение   представляет собой угловой коэффициент секущей ( .

Касательной к графику функции   в точке   называется предельное положение секущей  , при стремлении точки   по графику   к точке  .

Для того, чтобы секущая   при   стремилась к предельному положению, отличному от вертикальной прямой , необходимо и достаточно, чтобы существовал конечный предел  , то есть , чтобы существовала конечная производная функции   в точке  .

Угловой коэффициент касательной получается путем перехода от   к пределу при  :

Таким образом, получим, что  , где   - угол наклона касательной к оси  (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции   в точке   имеет вид

В случае бесконечной производной  .

Из уравнения секущей имеем:

Переходя в равенстве к пределу при  , получаем уравнение касательной к графику функции в точке   в виде  , то есть касательная является в данном случае вертикальной прямой, проходящей через точку   оси абсцисс.

Механический смысл производной

Пусть материальная точка движется прямолинейно и   - длина пути, проходимого за время  , отсчитываемого от некоторого момента времени  .

Для определения скорости   в данный момент   придадим переменной  некоторое приращение  , при этом приращение пути будет равно  .

Отношение   называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени  , и обозначается

Предел   называется величиной мгновенной скорости движения в момент времени  .

Таким образом, мгновенная скорость в момент времени   прямолинейного движения, совершаемого по закону   равна значению производной  .

Примеры задач

Задача 1. Составьте уравнение общей касательной к графикам функций   и  .

Решение.

I способ.

Прямая   является общей касательной графиков функций   и  , если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке.

- уравнение касательной к графику функции y=x² в точке с абсциссой x₀

- уравнение касательной к графику функции y=x³ в точке с абсциссой x₁

Прямые совпадают, если их угловые коэффициенты и свободные члены равны. Отсюда

Решением системы будут

Уравнения общих касательных имеют вид:

16) УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ К КРИВОЙ

Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку M(x₀, y₀), и составим уравнение касательной к данной кривой в точке M, предполагая, что эта касательная не параллельна оси Oy.

Уравнение прямой с угловым коэффициентом в общем виде есть у=kx+b. Поскольку для касательной k= f'(x₀), то получаем уравнение y= f'(x₀)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x₀, y₀).Поэтому ее координаты должны удовлетворять уравнению касательной: y₀= f'(x₀)·x₀ + b. Отсюда b=y₀– f'(x₀)·x₀.

Таким образом, получаем уравнение касательной y= f'(x₀)·x +y₀ – f'(x₀)·x₀ или

y = f '(x0)·(x – x0) + f(x0)

Если касательная, проходящая через точку М(x₀,y₀) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение x= x₀.

Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль.

Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.

И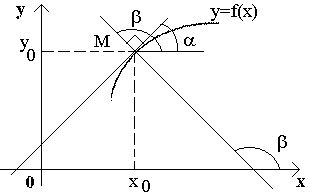 з определения нормали следует, что ее угловой коэффициент k_nсвязан с угловым коэффициентом касательной k равенством:

.

Учитывая, что нормаль также как и касательная проходит через точкуM(x₀, y₀), то уравнение нормали к кривой y= f(x) в данной точке M имеет вид:

Ясно, что если касательная параллельна оси Ox, т.е.f'(x₀) = 0 и ее уравнение имеет вид y= y₀, то нормаль в этой же точке будет перпендикулярна оси Ox. Значит, ее уравнение имеет вид x= x₀.

Примеры.

1. Составить уравнения касательной и нормали к графику функции у = tg²x в точке с абсциссой x₀=π/4.

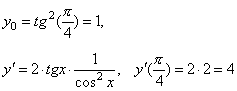
Уравнение касательной имеет вид y =4·(x – π/4) + 1 или y = 4x – π + 1.

Уравнение нормали будет y = –1/4·(x – π/4) + 1 или у = –1/4·x + π/16 + 1.

2. Составить уравнения касательной и нормали к графику функции у = 0.5·(x – 2)² + 5 в точке M(2; 5).

y'= x – 2, y'(2) = 0 . Следовательно, касательная параллельна оси Ox, а значит ее уравнение y= 5 . Тогда нормаль параллельна оси Oy и имеет уравнение x= 2 .

3. Найти уравнение касательной и нормали к эллипсу 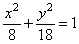  в точке M(2; 3).

Найдем y' по правилу дифференцирования неявной функции  .

Уравнение касательной:  ,т.е.  .

Уравнение нормали:  , т.е.  .

4. Составить уравнения касательной и нормали к циклоиде x= t – sin t, y= 1 – cos tв точке М(x₀; y₀), которая соответствует значению параметра t = π/2.

 При t=π/2x₀= π/2 – 1, y₀=1.

.

Уравнение касательной: y = x – π/2 + 1 + 1, т.е. у = x – π/2 + 2.

Уравнение нормали: y = – x – π/2 – 1 + 1, т.е. у = – x – π/2.