Бесконечно малая величина

Последовательность a_n называется бесконечно малой, если  . Например, последовательность чисел   — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x₀, если  .

Функция называется бесконечно малой на бесконечности, если   либо  .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то f(x) − a = α(x),  .

Если a_n — бесконечно малая последовательность, сохраняющая знак, то   — бесконечно большая последовательность.

• Бесконечно большая величина

• Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsin x, неограниченная с обеих сторон, не является бесконечно большой при  .

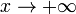• Последовательность a_n называется бесконечно большой, если  .

• Функция называется бесконечно большой в окрестности точки x₀, если  .

• Функция называется бесконечно большой на бесконечности, если   либо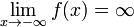 

связь между бесконечно малыми и большими функциями

   Если f (x) — бесконечно большая функция, то   есть бесконечно малая функция в этой же точке.    В самом деле, пусть  , это означает, что

• (  K > 0) (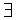  δ = δ(K)> 0) (  0 < | x - x₀ | < δ ) : | f (x) | > K .

   Так как |f (x)| > K , то 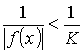 .  Будем считать, что  , тогда

(  ε > 0) (  δ = δ(ε)> 0) (  0 < | x - x₀ | < δ ) : 1/| f (x)| <ε .

• Это означает, что  .

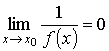6) Свойства бесконечно малых

• Сумма конечного числа бесконечно малых — бесконечно малая.

• Произведение бесконечно малых — бесконечно малая.

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если a_n — бесконечно малая последовательность, сохраняющая знак, то   — бесконечно большая последовательность.

Свойство 1. Произведение бесконечно малой функции     при    и функции   , ограниченной в некоторой   -окрестности точки  a, есть функция бесконечно малая.  Доказательство. Функция     является ограниченной в некоторой окрестности точки  a  и, следовательно, существует такое число  B > 0, что    (4)   для всех  x, удовлетворяющих условию    (5)         Поскольку функция     является бесконечно малой при   , то для любого произвольно малого числа  ε > 0 существует такое число   , что неравенство    (6)   выполняется для всех  x, удовлетворяющих условию      (7)   Выберем из чисел     и     наименьшее и обозначим его символом  δ. Тогда условие    (8)   является более сильным, чем условия (5) и (7) и поэтому влечет неравенства (4) и (6).        Таким образом, для любого произвольно малого числа  ε > 0  выполняется неравенство для всех  x  из  δ-окрестности точки  a. Свойство 2. Сумма двух бесконечно малых функций есть функция бесконечно малая.  Доказательство. Пусть  ε > 0  – произвольно малое число;     и     – бесконечно малые функции при   . Тогда существуют такие положительные числа     и   , что условия    (9)   и    (10)   влекут за собой соответствующие неравенства и       Если   , то условие     перекрывает оба условия (9) и (10) и, следовательно, Следствие. Сумма любого конечного числа бесконечно малых функций есть функция бесконечно малая.        Действительно, объединяя элементы такой суммы в группы по два слагаемых и заменяя сумму двух бесконечно малых одной бесконечно малой, получим сумму меньшего числа членов. В конечном итоге сумма любого конечного числа бесконечно малых будет сведена к одной бесконечно малой.

1. Функция

является бесконечно малой при   , поскольку представляет собой произведение ограниченной функции     и бесконечно малой   .

2. Функция     является бесконечно малой при   , ибо 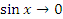    при   , а постоянный множитель может рассматриваться как частный случай ограниченной функции.

3. Выражение

представляет собой бесконечно малую при    поскольку каждое его слагаемое является бесконечно малой.

7)Сходящиеся последовательности и их свойства

Рассмотрим числовые последовательности.

Последовательность (x_n) действительных чисел называется сходящейся, если существует действительное число a и для произвольного ε > 0 существует натуральное число m такое, что для всех n > m справедливо неравенство |x_n - a| < ε.

При этом число a называют пределом последовательности (x_n), что символически записывают

 или x_n → a при n → ∞.

С помощью логических символов определение запишется следующим образом: числовая последовательность (x_n) называется сходящейся, если

Если последовательность не является сходящейся, то ее называют расходящейся.

Если последовательности (x_n) и (y_n) действительных чисел сходятся и  , то

8)

Необходимый признак сходимости последовательности. Необходимое и достаточное

условия сходимости монотонной последовательности. Примеры

9) Пусть имеется множество  , на котором введено отношение порядка.

Последовательность   элементов множества   называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.

 — неубывающая 

Последовательность   элементов множества   называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.

 — невозрастающая 

Последовательность   элементов множества   называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий.

 — возрастающая 

Последовательность   элементов множества   называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.

 — убывающая 

Последовательность называется монотонной, если она является неубывающей, либо невозрастающей.^[1]

Последовательность называется строго монотонной, если она является возрастающей, либо убывающей.

Очевидно, что строго монотонная последовательность является монотонной.

Иногда используется вариант терминологии, в котором термин «возрастающая последовательность» рассматривается в качестве синонима термина «неубывающая последовательность», а термин «убывающая последовательность» — в качестве синонима термина «невозрастающая последовательность». В таком случае возрастающие и убывающие последовательности из вышеприведённого определения называются «строго возрастающими» и «строго убывающими», соответственно.

Число эйлера

e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числомЭйлера или числом Непера. Обозначается строчной латинской буквой «e». Численное значение^[1]:

 (последовательность A001113 вOEIS)

Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.