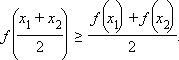Выпуклость функции и точки перегиба
Непрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x1 и x2 из этого отрезка
|
|
|
|
График 3.2.3.1. Выпуклая вверх функция |
Аналогично определяется функция, выпуклая вниз.
Дважды
дифференцируемая на [a; b] функция f (x) выпукла
вверх, если для любого 
|
Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого
|
Так,
вторая производная функции 
равна 
откуда
следует, что квадратичная функция
выпукла вниз на всей области определения.
Пусть
функция f (x) непрерывна
в точке 
и
имеет в этой точке конечную или бесконечную
производную. Тогда точка
называется точкой
перегиба функции f,
если в этой точке изменяется направление
ее выпуклости.
Необходимое условие наличия точки перегиба. Если – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то
|
Достаточные условия наличия точки перегиба.
Пусть
функция f (x) непрерывна
и имеет конечную или бесконечную
производную в точке 
Если 
меняет
знак при переходе через точку
то
–
точка перегиба функции f (x).
Если 
то
–
точка перегиба функции f (x).
В заключение приведем примеры, когда точка x0 не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:
если функция разрывна в точке (например
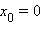);в случае угловой точки (например,
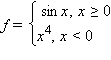
Не
являются точками перегиба и точки
возврата,
например точка 
у
функции 
Все вышеперечисленные случаи изображены на рисунке.
|
|
График 3.2.3.2.Точки, не являющиеся точками перегиба: точка разрыва, точка возврата, угловая точка |
32) Асимптоты графика функции
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
Определение 7.1 Вертикальной
асимптотой графика
функции 
называется
вертикальная прямая 
,
если 
или 
при
каком-либо из условий: 
, 
, 
.
Заметим, что мы при этом не требуем,
чтобы точка 
принадлежала
области определения функции 
,
однако она должна быть определена по
крайней мере в какой-либо из односторонних
окрестностей этой точки: 
или 
,
где 
.
Пример 7.1
Рассмотрим функцию 
.
График
имеет
вертикальную асимптоту 
,
поскольку при 
выполняется
условие 
,
а также при 
выполняется
условие 
.
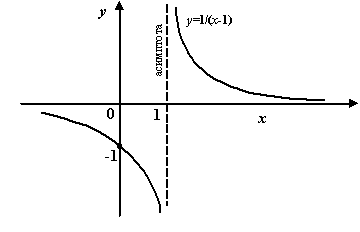
Рис.7.1.Вертикальная
асимптота функции 
Пример 7.2
Рассмотрим функцию 
.
Её график имеет вертикальную асимптоту 
,
так как 
при 
.
То, что при 
функция
не
стремится к бесконечности, для наличия
асимптоты неважно: для того, чтобы
прямая
являлась
вертикальной асимптотой, достаточно,
чтобы график приближался к ней хотя бы
с одной стороны. (К слову сказать, 
при
.)
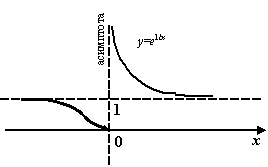
Рис.7.2.Вертикальная асимптота функции
Пример 7.3
Рассмотрим функцию 
.
Прямая
является
вертикальной асимптотой графика
,
так как
при
.
Заметим, что слева от точки
функция
вообще не определена.
Рис.7.3.Вертикальная асимптота функции
Итак, для нахождения вертикальных асимптот графика данной функции нужно исследовать точки разрыва функции и точки, лежащие на границах области определения функции, и выяснить, при приближении аргумента к каким из этих точек значения функции стремятся к бесконечности.
Наклонной
асимптотой графика
функции
при 
называется
прямая 
,
если выполнены два условия:
1)
некоторый луч 
целиком
содержится в 
;
2)
расстояние по вертикали между графиком
и прямой стремится к 0 при
:
|
(7.1) |
Наклонной
асимптотой графика
функции
при 
называется
прямая
,
если
1) некоторый луч 
целиком
содержится в
;
2)
расстояние по вертикали между графиком
и прямой стремится к 0 при
:
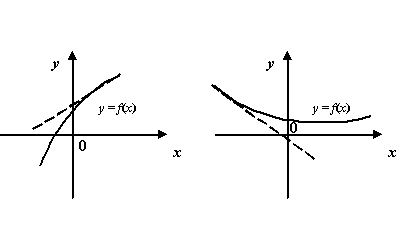
Рис.7.6.Графики функций, имеющие наклонные асимптоты при и при
В
случае, если наклонная асимптота
расположена горизонтально, то есть
при 
,
она называется горизонтальной
асимптотой.
Таким образом, горизонтальная асимптота --
частный случай наклонной асимптоты;
прямая 
является
горизонтальной асимптотой
графика
при
или
,
если
или
соответственно.
Пример 7.6
Рассмотрим функцию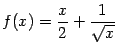 
.
График этой функции имеет наклонную
асимптоту 
при
.
Действительно,
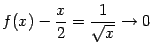при 
Однако эта функция не определена ни на каком луче вида , так что её график не может иметь асимптоты при .
Рис.7.7.Наклонная асимптота функции
Пример 7.7
График функции 
имеет
горизонтальную асимптоту 
как
при
,
так и при
,
поскольку, очевидно, 
при 
.
Можно сказать также, что асимптота
при
у
этого графика совпадает с асимптотой
при
.
Аналогично
определению наклонной асимптоты можно
дать также более общее определение:
Определение 7.3
Линия 
называется асимптотической
линией графика
функции
при
(или
при
),
если обе эти функции определены на
некотором луче
(или
луче
)
и разность ординат графиков стремится
к 0 при
(или
при
,
соответственно).
Если
функция 
--
линейная, то есть график
--
наклонная прямая, то асимптотическая
линия -- это наклонная асимптота.
Однако и другие линии бывает естественно
рассматривать в качестве асимптотических.
Пример 7.9
Рассмотрим функцию 
.
Так как 
при
,
то естественно рассматривать график 
как
асимптотическую линию при
для
графика исследуемой функции
.
Рис.7.10.Асимптотическая линия для графика функции при
Вернёмся
к наклонным асимптотам -- прямым
линиям с уравнением
.
Для их нахождения в тех случаях, когда
значения 
и 
не
очевидны, можно применять следующую
теорему.
Теорема 7.1 Прямая служит наклонной асимптотой для графика при (или при ) в том и только том случае, когда
|
И
|
(соответственно, если
и 
Таким образом, для нахождения наклонной (или горизонтальной, если получится ) асимптоты достаточно найти два указанных предела и, затем, . Прямая будет искомой асимптотой. Если же какой-либо из этих двух пределов не существует, то нет и соответствующей асимптоты.
Доказательство теоремы. Докажем теорему в случае ; доказательство при проводится совершенно аналогично.
Перепишем условие (7.1), задающее асимптоту, в виде
Так как первый множитель , то второй множитель, стоящий в квадратных скобках, должен быть бесконечно малым, то есть
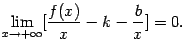
Но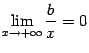 
и 
,
так что
откуда следует равенство (7.2). Теперь число уже известно.
Подставляя это число в формулу (7.1), находим, что
откуда следует равенство (7.3).
Пример 7.10
Найдём наклонные асимптоты графика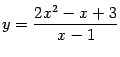 
.
Попробуем отыскивать сразу оба предела, и при , и при .
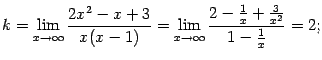
Итак,
и при
,
и при
имеем 
и 
,
так что обе наклонные асимптоты совпадают
друг с другом и имеют уравнение 
,
то есть, фактически, асимптота только
одна.
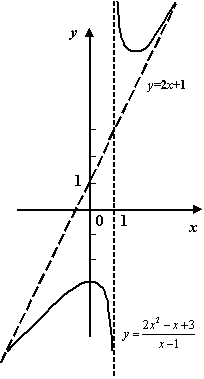
Рис.7.11.График и его наклонная асимптота
Замечание 7.2 Из определения асимптоты не следует, что если асимптоты при и при для одного и того же графика существуют, то они непременно совпадают. Это могут быть и различные прямые, как показывает следующий простой пример.
Пример 7.11
Рассмотрим график 
.
При
график
приближается к горизонтальной асимптоте 
,
а при
--
к другой горизонтальной асимптоте 
.
Рис.7.12.График арктангенса имеет две разных горизонтальных асимптоты
Различными могут оказаться и не обязательно горизонтальные асимптоты:
Пример 7.12
Рассмотрим функцию 
.
Покажем, что обе её наклонные асимптоты
существуют, но не совпадают друг с
другом.
Сначала найдём асимптоту при . Согласно доказанной теореме, имеем:
Таким
образом, при
наклонной
асимптотой служит прямая 
.
Теперь найдём асимптоту при . Имеем:
Поскольку
,
мы можем считать, что в допредельном
выражении 
.
В полученной дроби поделим числитель
и знаменатель на положительное число 
.
Тогда под корнем нужно будет поделить
на 
,
и получится:
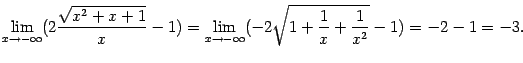
Вычисление
проведите
сами в качестве упражнения. При этом
получается 
,
так что наклонная асимптота при
имеет
уравнение 
.
Рис.7.13.График 
и
его две наклонных асимптоты
Замечание 7.3 Если график имеет асимптоту (например, при ) и существует предел производной:
то 
.
Иными словами, если угловой коэффициент
касательной имеет предел, то этот предел
равен угловому коэффициенту асимптоты17.
Однако
асимптота может существовать и в случае,
когда производная 
не
имеет никакого предела при
.
Дело в том, что значения
могут
совершать мелкие, но частые колебания
относительно ординаты асимптоты, так
что значения производной могут при этом
испытывать незатухающие колебания.
Проиллюстрируем эту возможность
следующим примером
33)
Различные виды неопределенностей
Бесконечно малые величины имеют фундаментальное значение в математическом анализе. Например, понятие предела функции можно сформулировать, положив в основу концепцию бесконечно малой функции. Бесконечно большая функция представляет собой величину, обратную бесконечно малой. Фактически любой раздел дифференциального и интегрального исчисления опирается на анализ бесконечно малых. Концепция эквивалентных бесконечно малых функций позволяет существенно упростить процедуру раскрытия неопределенностей различного вида и свести вычисление пределов сложных выражений к тривиальным преобразованиям комбинаций степенных функций. Перечислим основные формы неопределенностей:
Под
неопределенностью вида 
понимается отношение двух бесконечно
малых величин. Неопределенность вида
возникает при делении одной бесконечно
большой величины на другую. Аналогично
интерпретируются и другие формы
неопределенностей.
Любая форма неопределенности может
быть преобразована к неопределенности
вида
.
Действительно, пусть
и 
– бесконечно большие функции в окрестности
некоторой точки. Тогда
Аналогично,
Для преобразования форм неопределенностей
к виду 
(и, следовательно, к виду
)
можно использовать логарифмическое
тождество
Пусть,
например, 
и 
при x → a.
Тогда
Аналогично,
Раскрытие
неопределенностей вида 
и 
по
правилу Лопиталя
(если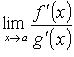 
существует).