
- •Основные элементарные функции
- •Бесконечно малая величина
- •6) Свойства бесконечно малых
- •Способы определения
- •Свойства
- •Предел функции по Коши
- •Окрестностное определение по Коши
- •Точки разрыва
- •17) Правила дифференцирования
- •Свойства дифференциала аналогичны свойствам производной.
- •Дифференцируемость функций. Непрерывность дифференцируемой функции
- •24,25,26,27) Разложение некоторых элементарных функций по формуле Маклонена
- •30) Достаточные условия существования локальных экстремумов
- •Выпуклость функции и точки перегиба
- •32) Асимптоты графика функции
- •Предел функции, правило Лопиталя.
- •Общая схема исследования функции и построения ее графика
- •Свойства первообразной
- •38) Непосредственное интегрирование
24,25,26,27) Разложение некоторых элементарных функций по формуле Маклонена
 ,
,
 ,
,
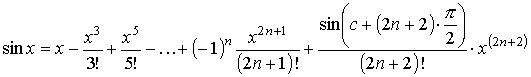 ,
,
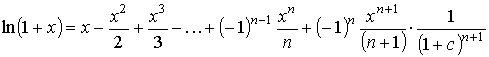 ,
,

Формула
Тейлора является эффективным средством
для вычисления пределов функций, с
которыми часто приходится иметь дело
при исследовании функций.
Пример 1. Вычислить
предел ![]() .
Решение.
Используя разложение функции sin x,
имеем
.
Решение.
Используя разложение функции sin x,
имеем
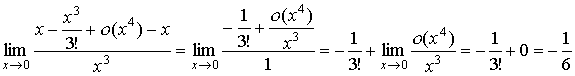
Пример
2. Вычислить
предел 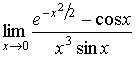 .
Решение.
Используя разложения функций, входящих
в выражение предела, имеем
.
Решение.
Используя разложения функций, входящих
в выражение предела, имеем
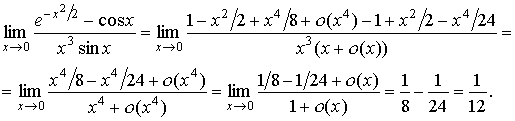
Разложить в ряд Маклорена функцию()xfxe- ответ в тетради!
Разложить в ряд Маклорена функцию. ()sinfxx=???
Разложить в ряд Маклорена функцию. ()cosfxx=???
Разложить в ряд Маклорена функцию. ()ln(1)fxx=+???
28) Признак монотонности функции
Промежутки монотонности функции совпадают с промежутками постоянного знака ее производной.
Доказательство. Будем
понимать заданную функцию у
= f(x) как
закон движения материальной точки
Р
по оси у
в зависимости от времени х.
Пусть на некотором промежутке функция f
возрастает. На языке механики это
означает, что материальная точка Р
движется по оси у
в положительном направлении.
Так как знак скорости совпадает с
направлением движения, то скорость
точки, т. е. производная функции
положительна.
Обратно: если производная,
т. е. скорость точки, положительна, то
точка движется по оси у в
положительном направлении, следовательно,
функция возрастает.
Аналогично
рассматривается случай убывания функции.
Замечание. Если
точка движется в одном направлении, то
ее скорость сохраняет постоянный знак,
однако в отдельные моменты времени
точка может остановиться (ее скорость
обратится в нуль), а затем продолжать
двигаться в том же направлении. Функция,
описывающая такое движение точки, будет
монотонной. Значит,
если f(x) возрастает,то f'(x)
> 0.
Верно и обратное. Однако
если f'(x) обращается
в нуль не в отдельных точках, а на целом
промежутке, то на этом промежутке функция
будет постоянной. Если включить промежутки
постоянства функции в промежутки ее
монотонности (как иногда говорят, не
требовать строгой монотонности функции),
то можно коротко результат исследования
записать так: ![]()
.
29. Необходимое условие существования локального экстремума для функции
Пусть
задана функция z
=z (x,y), (x,y)![]() D.
Точка M0(x0;y0
D -
точка локального экстремума.
D.
Точка M0(x0;y0
D -
точка локального экстремума.
Если в этой точке существуют z'x и z'y, то

Геометрическое доказательство "очевидно". Если в точке C0 на (рис.1.4) провести касательную плоскость, то она "естественно" пройдет горизонтально, т. е. под углом 0° к оси Ох и к оси Оу.
Тогда в соответствии с геометрическим смыслом частных производных (рис.1.3):
![]()
что и требовалось доказать.
Определени
Если в точке M0 выполняются условия (1.41), то она называется стационарной точкой функции z (x,y).
30) Достаточные условия существования локальных экстремумов
Пусть функция
 непрерывна
в
непрерывна
в 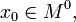 и
существуют конечные или бесконечные
односторонние производные
и
существуют конечные или бесконечные
односторонние производные 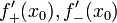 .
Тогда при условии
.
Тогда при условии
![]()
x0 является точкой строгого локального максимума. А если
![]()
то x0 является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке x0
Пусть функция f непрерывна и дважды дифференцируема в точке x0. Тогда при условии
![]() и
и ![]()
x0 является точкой локального максимума. А если
и ![]() то x0 является
точкой локального минимума
то x0 является
точкой локального минимума
31)
