- •Основные элементарные функции
- •Бесконечно малая величина
- •6) Свойства бесконечно малых
- •Способы определения
- •Свойства
- •Предел функции по Коши
- •Окрестностное определение по Коши
- •Точки разрыва
- •17) Правила дифференцирования
- •Свойства дифференциала аналогичны свойствам производной.
- •Дифференцируемость функций. Непрерывность дифференцируемой функции
- •24,25,26,27) Разложение некоторых элементарных функций по формуле Маклонена
- •30) Достаточные условия существования локальных экстремумов
- •Выпуклость функции и точки перегиба
- •32) Асимптоты графика функции
- •Предел функции, правило Лопиталя.
- •Общая схема исследования функции и построения ее графика
- •Свойства первообразной
- •38) Непосредственное интегрирование
1)числовая
функция —
это функция,
области определения и значений которой
являются подмножествами числовых
множеств — как правило,
множества вещественных
чисел ![]() или
множества комплексных
чисел
или
множества комплексных
чисел ![]() .
.
Способы задания функции
Словесный |
С помощью естественного языка |
Игрек равно целая часть от икс. |
||||||||||||||||||||||
Аналитический |
С помощью формулы и стандартных обозначений |
f(x) = x! |
||||||||||||||||||||||
Графический |
С помощью графика |
Фрагмент
графика функции |
||||||||||||||||||||||
Табличный |
С помощью таблицы значений |
|
Аналитический способ
Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента.
Примеры:
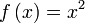 ;
;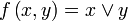 ;
;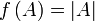 ;
;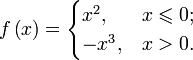
Табличный способ
Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Графический способ
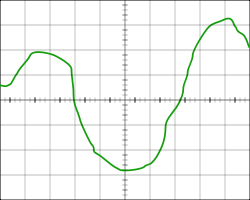
Осциллограмма задаёт значение некоторой функции графически.
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостаткаточности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.
Рекурсивный способ
Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.
Примеры:
факториал;
числа Фибоначчи;
функция Аккермана.
Словесный способ
Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.
Примеры:
Факториал
Возвращает произведение всех натуральных чисел, не больших данного. Кроме того,
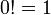 .
.
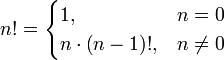
Область определения:
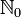 (множество натуральных
чисел с
нулём).
(множество натуральных
чисел с
нулём).Область значений:
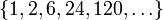
2) Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
Областью
значений функции ![]() ,
непрерывной на отрезке
,
непрерывной на отрезке ![]() ,
является отрезок
,
является отрезок ![]() где
минимум и максимум берутся по отрезку
.
где
минимум и максимум берутся по отрезку
.
Если
функция
непрерывна
на отрезке
и ![]() то
существует точка
то
существует точка ![]() в
которой
в
которой ![]() .
.
Если
функция
непрерывна
на отрезке
и
число ![]() удовлетворяет
неравенству
удовлетворяет
неравенству ![]() или
неравенству
или
неравенству ![]() то
существует точка
в
которой
то
существует точка
в
которой ![]() .
.
Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
Монотонная функция на отрезке непрерывна в том и только в том случае, когда область ее значений является отрезком с концами
 и
и 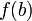 .
.Если функции и
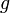 непрерывны
на отрезке
,
причем
непрерывны
на отрезке
,
причем 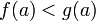 и
и 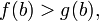 то
существует точка
в
которой
то
существует точка
в
которой 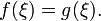 Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
Примеры
Элементарные функции
Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.
[править]Функция с устранимым разрывом
Функция ![]() задаваемая
формулой
задаваемая
формулой
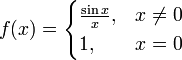
непрерывна
в любой точке ![]() Точка x =
0 является
точкой устранимого разрыва, ибо предел
функции
Точка x =
0 является
точкой устранимого разрыва, ибо предел
функции
![]()
[править]Функция знака
Функция
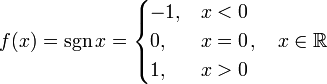
называется функцией знака.
Эта
функция непрерывна в каждой точке ![]() .
.
Точка x = 0 является точкой разрыва первого рода, причём
![]() ,
,
в то время как в самой точке функция обращается в нуль.
Ступенчатая функция
Ступенчатая функция, определяемая как
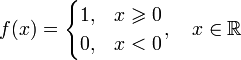
является всюду непрерывной, кроме точки x = 0, где функция терпит разрыв первого рода. Тем не менее, в точке x = 0 существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, ступенчатая функция является примером непрерывной справа функции на всей области определения.
Аналогично, ступенчатая функция, определяемая как
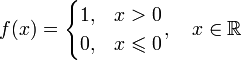
является примером непрерывной слева функции на всей области определения.
3) Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
Основные элементарные функции
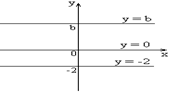
1) Постоянная функция: y = b.
|
Графиком постоянной функции y = b является прямая, параллельная оси абсцисс и проходящая через точку (0; b) на оси ординат.
|
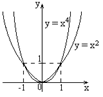
2) Степенная функция.
а)
Степенная функция с натуральным
показателем![]() (n – натуральное число:
(n – натуральное число: ![]() ).
(непериодическая)
).
(непериодическая)
n – четное число О Область
значений Монотонность: убывает
на Четная.
|
n – нечетное число
О Область значений .
Монотонность:
возрастает на Нечетная. |
б)
Степенная функция с целым отрицательным
показателем ![]() (n
– натуральное число:
).
(непериодическая)
(n
– натуральное число:
).
(непериодическая)
n – четное число О Область
значений Монотонность: возрастает
на Четная. |
n – нечетное число О Область
значений Монотонность: убывает
на Нечетная. |
в)
Степенная функция с положительным
показателем меньше единицы ![]() (n
– натуральное число больше единицы:
;
(n
– натуральное число больше единицы:
;![]() ).
(непериодическая).
).
(непериодическая).
n – четное число О Область значений . Монотонность: возрастает
на Общего вида. |
n – нечетное число О Область
значений Монотонность: возрастает
на Нечетная. |
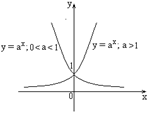
3) Показательная
функция ![]()
![]() .(непериодическая).
.(непериодическая).
|
Область
определения Область значений . Монотонность: возрастает
на
,
если Общего вида. |
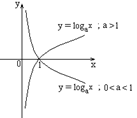
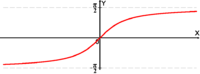
4) Логарифмическая
функция ![]() .(непериодическая).
.(непериодическая).
|
Область
определения Область
значений Монотонность: возрастает
на Общего вида. |
4)
Число ![]() называется пределом
числовой последовательности
называется пределом
числовой последовательности ![]() ,
если последовательность
,
если последовательность ![]() является
бесконечно малой, т. е. все её элементы,
начиная с некоторого, по модулю меньше
любого заранее взятого положительного
числа.
является
бесконечно малой, т. е. все её элементы,
начиная с некоторого, по модулю меньше
любого заранее взятого положительного
числа.
![]()
Геометрический смысл предела числовой последовательности
Число a – предел
последовательности xn, если в любую
окрестность числа а, начиная с некоторого
номера попадают все члены последовательности
![]() .
.
Теорема "Об единственности пределов"
Посл-ть не может иметь больше одного предела.
Док-во (от противного)
{xn} имеет два разл. предела a и
b (a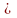 b).
b).
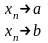 .
По определению существует такое число
.
По определению существует такое число
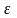 >0,
что
>0,
что
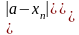 Получается, что
Получается, что
 ,
т.е. a=b.
,
т.е. a=b.
Для того, чтобы функция f (x) при x → a стремилась к конечному пределу A , необходимо и достаточно, чтобы функция α (x) = f (x) − A была бесконечно малой в точке a .
Доказательство. Необходимость. Если lim x→a f (x) = A , то
∀ε > 0 ∃δ > 0: ∀x ∈ Rδ (a) {a} ⇒ f (x) − A < ε .
Очевидно, что f (x) − A < ε ⇒ α (x) − 0 < ε . Откуда немедленно следует, что
lim x→a α (x) = 0 .
Достаточность. Если lim x→a f(x) = 0 , то
∀ε > 0 ∃δ > 0: ∀x ∈ Rδ (a) {a} ⇒ α (x) − 0 < ε .
Так как α (x) − 0 < ε ⇒ f (x) − A < ε , то это и означает, что lim x→a f (x) = A .
Доказанную теорему можно сформулировать иначе: функция f (x) при
x → a стремится к конечному пределу A тогда и только тогда, когда f (x)
равна сумме числа A и некоторой функции α (x) , бесконечно малой в точке a
f (x) = A + α (x).
Теорема о единственности предела: Числовая последовательность может иметь только один предел
5) Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.

 бласть
определения
бласть
определения 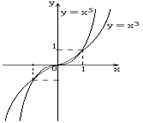 бласть определения
бласть определения  бласть
определения
бласть
определения 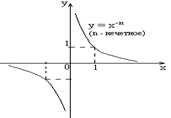 бласть
определения
бласть
определения 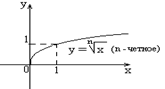 бласть
определения
бласть
определения  бласть
определения
бласть
определения